Содержание
- 2. a2 + b2 = c2 Теорема Пифагора В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов
- 3. log x y = log x + log y Логарифм и логарифмическая шкала Использование в вычислениях
- 4. df f(t+h) ̶ f(t) dt h = lim h→0 Формула Ньютона-Лейбница Формула Ньютона - Лейбница, или
- 5. m1m2 r2 F = G Закон всемирного тяготения Ньютона Закон, описывающий гравитационное взаимодействие между двумя материальными
- 6. i 2 = ̶ 1 Комплексное число Идея о необходимости расширения понятия действительного числа возникла в
- 7. F ̶ E + V = 2 Эйлерова характеристика Характеристика топологического пространства, которая является важным инструментом
- 8. 1 √2πσ Ф(x) = e (x – μ)2 2σ2 Нормальное распределение Если результат наблюдения является суммой
- 9. ∂2u ∂2u ∂t2 ∂x2 = c 2 Волновое уравнение Волновое уравнение - дифференциальное уравнение с частными
- 10. Преобразование Фурье Преобразование Фурье - операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Уравнение используется
- 11. p + υ ∙ υ = ̶ p + ∙ T + f ∂υ ∂t (
- 12. ∙ E = 0 x E = ̶ ∂H ∂t 1 c ∙ H = 0
- 13. d S ≥ 0 Второе начало термодинамики Физический принцип, накладывающий ограничение на направление процессов передачи тепла
- 14. E = m c2 Теория относительности Научная теория, объясняющая устройство мира на макроуровне, объединяющая механику, электродинамику
- 15. iћ Ψ = Ĥ Ψ ∂ ∂t Уравнение Шрёдингера Уравнение, описывающее изменение в пространстве и во
- 16. H = ̶ p(x) log p(x) Раздел прикладной математики, радиотехники (теория обработки сигналов), информатики, аксиоматически определяющий
- 17. xt+1 = k xt(1 ̶ xt) Логистическое уравнение Уравнение изначально появилось при рассмотрении модели роста численности
- 19. Скачать презентацию
















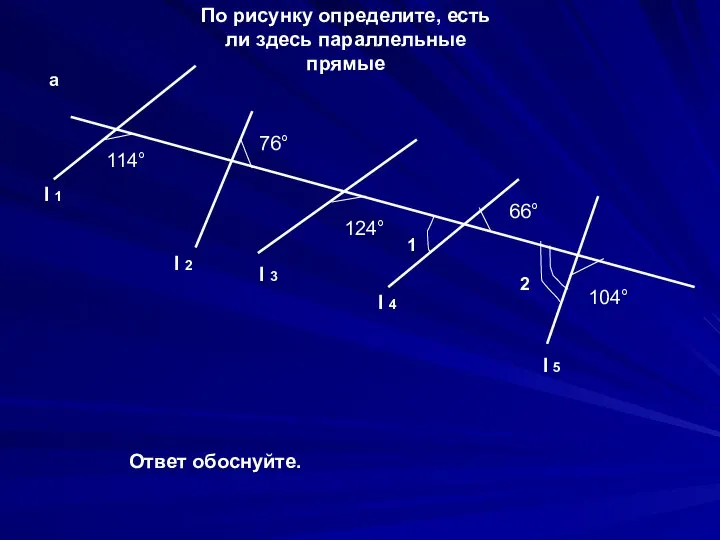 Параллельные прямые
Параллельные прямые Построение желаемой ЛАЧХ разомкнутой системы в частотном методе синтеза корректирующего звена
Построение желаемой ЛАЧХ разомкнутой системы в частотном методе синтеза корректирующего звена Деление с остатком
Деление с остатком Деление на трехзначное число
Деление на трехзначное число Решение тригонометрических уравнений
Решение тригонометрических уравнений Распределительное свойство умножения
Распределительное свойство умножения Несобственные интегралы. Геометрические приложения определенного интеграла
Несобственные интегралы. Геометрические приложения определенного интеграла Основные постулаты
Основные постулаты Тренажёр. Таблица умножения
Тренажёр. Таблица умножения Одночлены. Обобщающий урок
Одночлены. Обобщающий урок Параллельное и последовательное соединения
Параллельное и последовательное соединения Презентация на тему Расстояние от точки до прямой
Презентация на тему Расстояние от точки до прямой  Таблица умножения на 3
Таблица умножения на 3 Математика. Числа до 20
Математика. Числа до 20 Как построить график функции y=f(x)+m, если известен график функции y=f(x)
Как построить график функции y=f(x)+m, если известен график функции y=f(x) Час занимательной математики. 5 класс
Час занимательной математики. 5 класс Математические ребусы
Математические ребусы Определение стоимости проезда пассажира на железнодорожном транспорте. Задания
Определение стоимости проезда пассажира на железнодорожном транспорте. Задания Решение задач по теме Параллелограмм
Решение задач по теме Параллелограмм Степень числа
Степень числа Свойства параллельных плоскостей (10 класс)
Свойства параллельных плоскостей (10 класс) Два обыкновенных дифференциальных уравнения
Два обыкновенных дифференциальных уравнения Дифференциальное исчисление
Дифференциальное исчисление Жили-были числа
Жили-были числа Цифра 3
Цифра 3 Геометрия вокруг нас
Геометрия вокруг нас Матрицы. Основные понятия
Матрицы. Основные понятия Аксиомы стереометрии и их следствия
Аксиомы стереометрии и их следствия