Доверительный интервал косвенных измерений

Косвенное измерение – определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной.
При косвенных измерениях искомое значение величины Q рассчитывают на основании известной функциональной зависимости этой величиной от величин, подвергаемых прямым измерениям.
Q = F (X, Y, …, Z),
где X, Y,…, Z – результаты прямых измерений соответствующих величин.
Принципиальной особенностью косвенных измерений является обработка (преобразование) результатов вне прибора (вручную или автоматически с помощью компьютера). Характерным признаком косвенных измерений является процедура выбора косвенной зависимости Q = F (X, Y, …, Z). Имеется в виду подтверждение степени адекватности принятой идеализированной модели связи величин фактическим значениям искомой величины.

Примерами косвенных измерений можно рассматривать:
определение площади сечения S арматурного стержня круглого сечения (см. рис.) по данным измерения его диаметра: искомая величина – площадь сечения S , косвенный параметр – диаметр d. В данном случае мы имеем однопараметровые косвенные измерения
определение площади помещения S по данным измерения его длины a и ширины b
S = a · b .
в этом случае мы имеем многопараметровые косвенные измерения (два параметра – а и b)
В общем случае ситуацию с косвенными измерениями можно формализовать следующим образом
y = F(x, z,…,q) , где y – искомая величина, x, z,…,q – косвенные величины (параметры)
Независимо от числа параметров, результат должен быть представлен доверительным интервалом по стандартной форме
y = y0 ± Δy
где y0 – точечная оценка, Δy – полуширина доверительного интервала

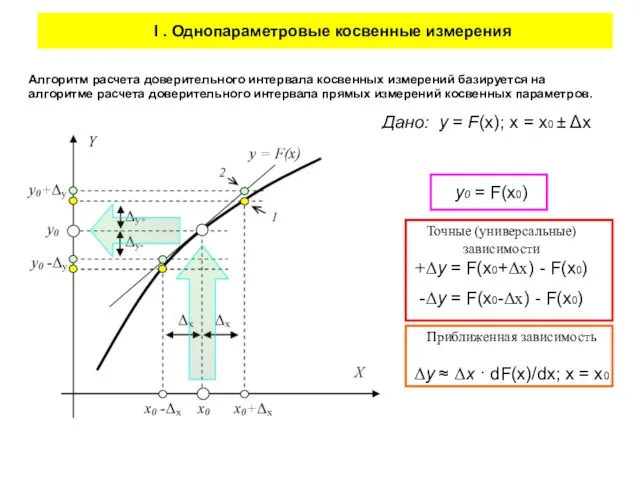
Алгоритм расчета доверительного интервала косвенных измерений базируется на алгоритме расчета доверительного интервала прямых измерений косвенных параметров.
I . Однопараметровые косвенные измерения
Дано: y = F(x); x = x0 ± Δx
y0 = F(x0)
Точные (универсальные) зависимости
+Δy = F(x0+Δx) - F(x0)
-Δy = F(x0-Δx) - F(x0)
Приближенная зависимость
Δy ≈ Δx · dF(x)/dx; x = x0

Разница результатов расчета доверительного интервала Δy по точной и приближенной зависимостям зависит от степени «кривизны» функциональной зависимости и от ширины доверительного интервала для x - ±Δx.
В подавляющем большинстве практических случаев, и учитывая необходимость округления доверительного интервала, разницу расчетных значений доверительного интервала по точной формуле и по приближенной можно не принимать во внимание.
!
Приближенная формула особенно удобна в случаях, когда связь между y и x выражается степенной функцией, то есть
В этом случае
Воспользуемся представлением доверительного интервала в относительных показателях

В этом случае можно записать
!
Относительная погрешность искомой величины y будет в B раз больше относительной погрешности косвенной величины x
Например, требуется определить доверительный интервал оценки объема V шара, если величина его диаметра 1). D = 15±1 см . 2). D = 15,0±0,1 см .
Расчет точечной оценки объема шара V0.
Исходя из формулы объема шара можем записать:
Вариант решения 1. Используем точную формулу расчета ΔV.
Исходя из формулы объема шара можем записать:
D = 15±1 см

Для D = 15,0±0,1 см получим следующие значения ΔV:
D = 15,0±0,1 см
Вариант решения 2. Используем приближенную формулу расчета ΔV, учитывая, что связь объема и диаметра выражается степенной функцией
D = 15±1 см
Для D = 15,0±0,1 см получим следующие значения ΔV:
D = 15,0±0,1 см

II . Многопараметровые косвенные измерения
.Требуется записать выражение для доверительного интервала Y в стандартном виде:
Y = y0 ± Δy (1)
Дано: Известен доверительный интервал для величин X, Z, Q,…,S записанный в стандартном виде:
X = x0 ± Δx ;
Z = z0 ± Δz ;
Q = q0 ± Δq ;
…
S = s0 ± Δs ;
известна функциональная зависимость
.
Порядок расчета следующий:
Рассчитывается точечная оценка y0 результата косвенных измерений
величины Y путем подстановки в выражение (1) для косвенной величины Y
точечные оценки результатов измерения аргументов, то есть
y0 = F (x0, z0, q0, …,s0), (2)

2. Рассчитываются составляющие доверительного интервала по каждому параметру
Границы доверительного интервала для Y можно определить из выражений:
Δyx = |F [(x0 + Δx), z0, q0, …,s0] - y0|
Δyz = |F [x0, (z0+ Δz), q0, …,s0] - y0| (3)
Δyq = |F [x0, z0, (q0+ Δq), …,s0] - y0|
...
Δys = |F [x0, z0, q0, …,(s0+ Δs)] - y0|
.Каждая составляющая погрешности расчитывается так же, как погрешность однопараметровых косвенных измерений, рассматривая F поочередно, как функцию одного параметра: x, затем z, q, и s.
3.Составляющие дов.интервала объединяются геометрическим
суммированием, то есть
(4)

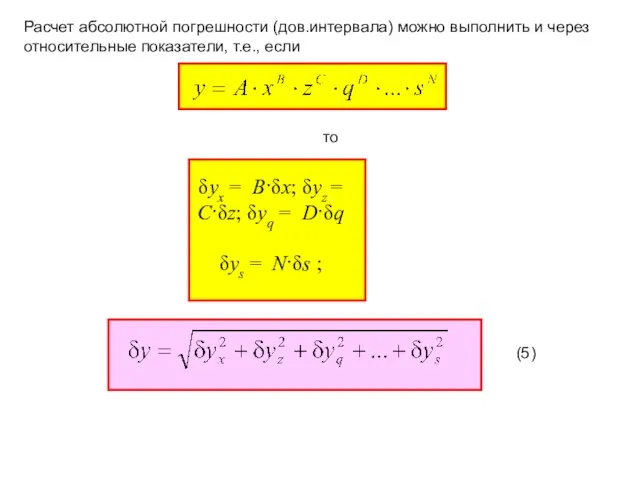
Расчет абсолютной погрешности (дов.интервала) можно выполнить и через
относительные показатели, т.е., если
то
δyx = B·δx; δyz = C·δz; δyq = D·δq
δys = N·δs ;
(5)

Расчетная формула
S = a· b
результат следует записать по форме:
S = S0 ± ΔS
погрешность площади будет иметь две составляющие ΔSa и ΔSb , которые объединяются геометрическим суммированием
Пример 2. Рассчитать площадь сечения колонны по известным значениям
линейных размеров сечения
a = 253,429 ± 2,145 мм после округления a = 253,4 ± 2,1 мм
b = 248,333 ± 2,039 мм b = 248,3 ± 2,0 мм
±ΔSa = (a0 ± Δa)·b – S0 = ±Δa·b = 2,145 · 248,33 = 532,68
±ΔSb = (b0 ± Δb)·a – S0 = ±Δb·a = 2,039 · 253,43 = 516,74
S0 = a0· b0 = 253,43 · 248,33 =62934,3

Объединяем составляющие
Записываем результат S = 62934,3 ± 742,1
После округления S = 62900 ± 700 или S = 62950 ± 750
Вариант расчета 2. Поскольку функциональная зависимость для площади является степенной функцией, то для расчета составляющих общей погрешности можно воспользоваться формулами для относительных погрешностей
После округления S = 62900 ± 700 или S = 62950 ± 750

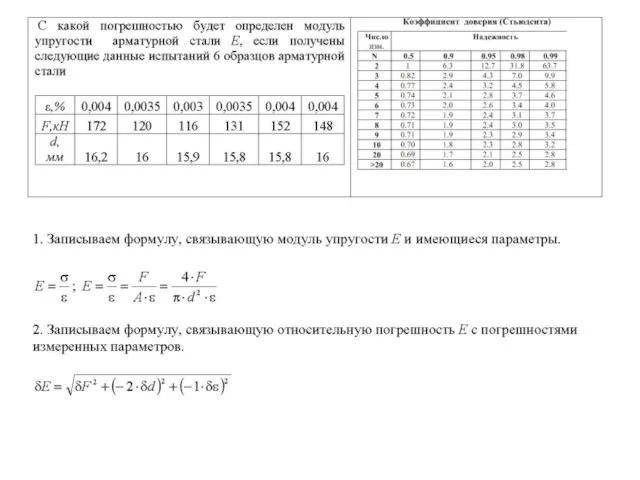
Пример 3.5 . Рассчитать доверительный интервал (относительную погрешность) оценки объема помещения,
если относительная погрешности оценки его высоты δh = 2% , а относительные погрешности длины a и ширины b равны δa = δb = 1%.
Решение. Выражение для объема помещения V представляет собой степенную функцию трех параметров – длины, ширины и высоты
поэтому расчет относительной погрешности объема выполним по формуле
.Подставляя значения относительных погрешностей линейных размеров, получаем относительную погрешность объема
Рассчитаем погрешность объема «по частям», сначала определим дов.интервал площади основания S
,
затем определим дов. интервал объема

Подставляя известные значения относительных погрешностей, получаем относительную погрешность высоты
Частная погрешность - δh превосходит погрешность объема (2,5%) и не согласуется с данными примера 3.5 , где относительная погрешность высоты δh ≈ 2% !
Результат неверный !!!
Для верного решения необходимо воспользоваться формулой, в которой нет необходимости учитывать корреляцию