Содержание
- 2. Определение производной Пусть функция y = f(x) определена в некотором интервале (a; b). Аргументу x придадим
- 3. Определение производной Итак, по определению: Функция y = f(x) , имеющая производную в каждой точке интервала
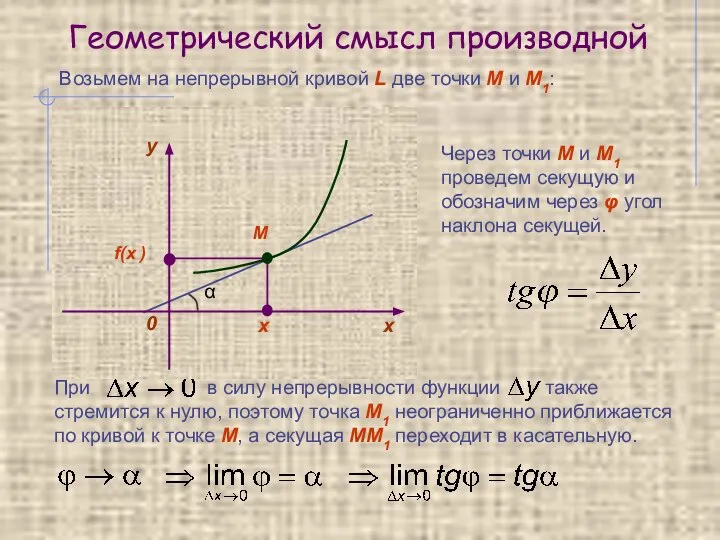
- 4. Геометрический смысл производной Возьмем на непрерывной кривой L две точки М и М1: х f(x )
- 5. Геометрический смысл производной Производная f ’(x) равна угловому коэффициенту касательной к графику функции y = f(x)
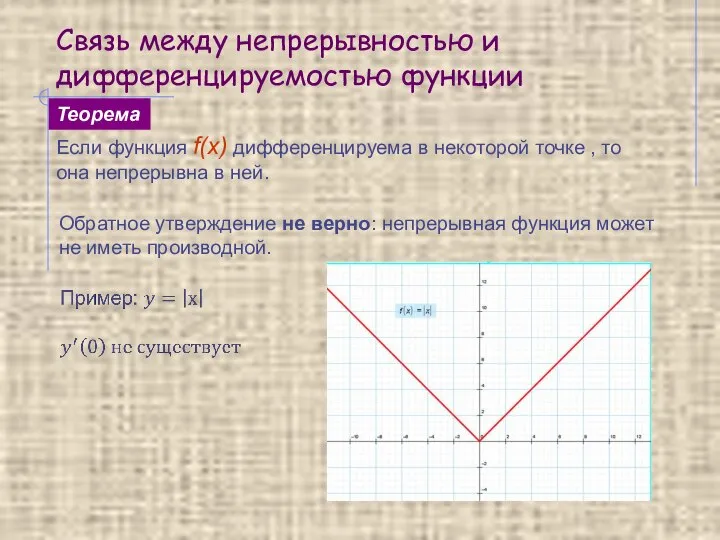
- 6. Связь между непрерывностью и дифференцируемостью функции Если функция f(x) дифференцируема в некоторой точке , то она
- 7. Таблица производных
- 8. Правила дифференцирования Пусть u(x) , v(x) и w(x) – дифференцируемые в некотором интервале (a; b) функции,
- 9. Производная сложной функции Пусть y = f(u) и u = φ(x) , тогда y = f(φ(x))
- 10. Пример. Вычислить производную функции
- 11. Пример. Вычислить производную функции Данную функцию можно представить следующим образом: Коротко:
- 12. Производные высших порядков Итак: Производной n – ого порядка (или n – ой производной) называется производная
- 13. Производные высших порядков - производная пятого порядка. Начиная от производной 4 порядка , производные обозначаются римскими
- 14. Производные от функций, заданных параметрически Производная первого порядка от этой функции находится по формуле: Пусть функция
- 15. Производные от функций, заданных параметрически Вычислить производную 3 – ого порядка от функции:
- 16. Дифференциал функции Пусть функция y = f(x) имеет в некоторой точке х отличную от нуля производную,
- 17. Дифференциал функции Дифференциалом функции y = f(x) в точке х называется главная часть ее приращения: Дифференциал
- 18. Геометрический смысл дифференциала Проведем к графику функции y = f(x) в точке М(x, y) касательную х
- 19. Приложение дифференциала в приближенных вычислениях Как известно, приращение функции можно представить в виде: Это равенство позволяет
- 20. Приложение дифференциала в приближенных вычислениях Вычислить приближенно: Рассмотрим функцию: Так как то
- 21. Исследование функций с помощью производной и построение графиков функций Схема 1. Найти о.о.ф. 2. Найти (если
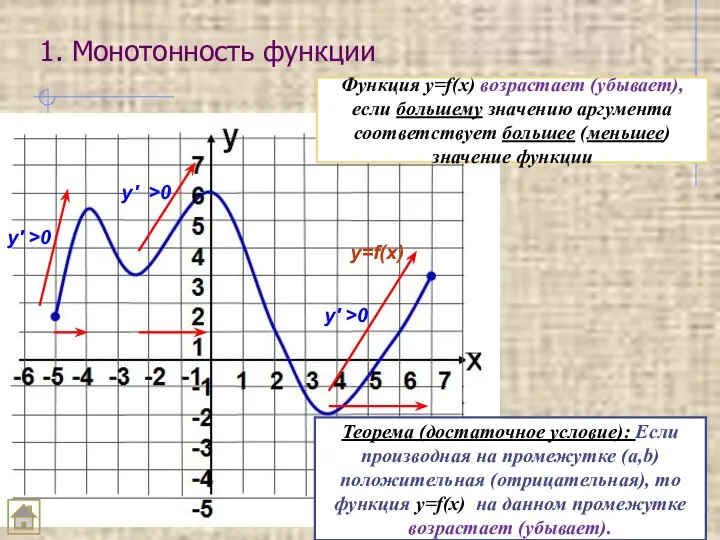
- 22. 1. Монотонность функции Функция y=f(x) возрастает (убывает), если большему значению аргумента соответствует большее (меньшее) значение функции
- 23. Точки экстремума
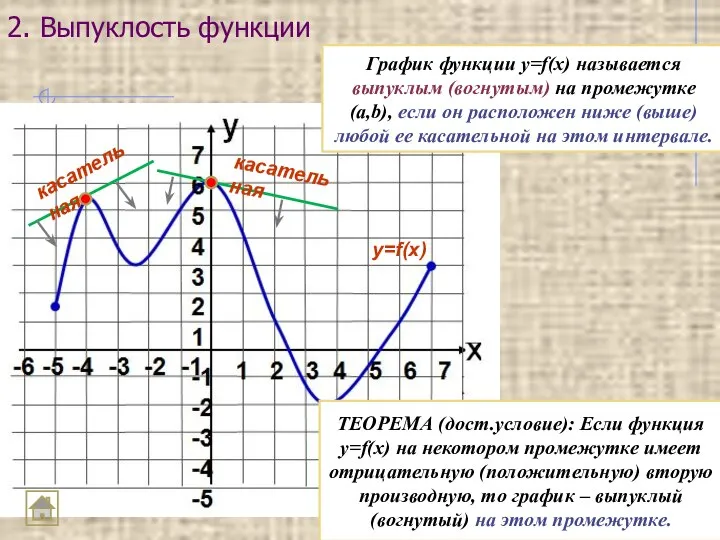
- 24. 2. Выпуклость функции График функции y=f(x) называется выпуклым (вогнутым) на промежутке (a,b), если он расположен ниже
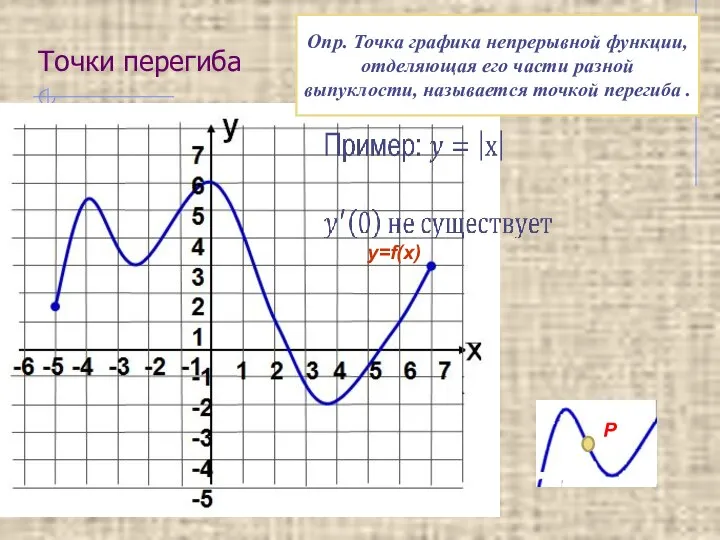
- 25. Точки перегиба P1 Опр. Точка графика непрерывной функции, отделяющая его части разной выпуклости, называется точкой перегиба
- 26. Асимптоты графика функции Опр. Прямая называется асимптотой графика функции, если расстояние от точек графика до этой
- 28. Скачать презентацию




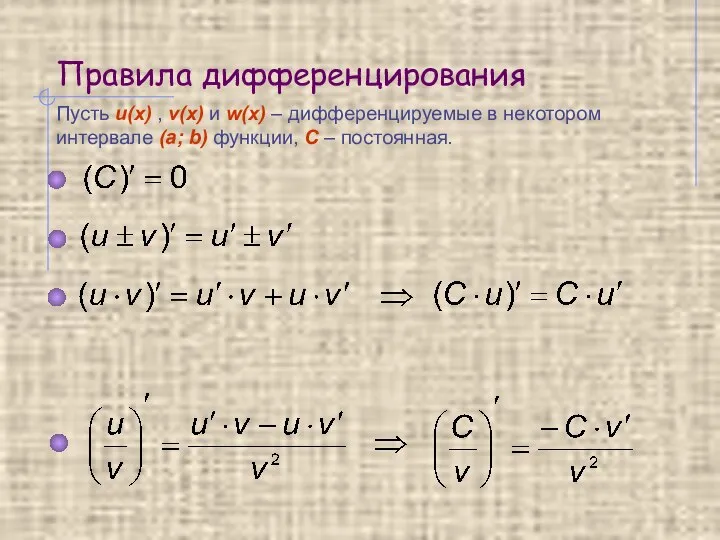















 Логарифмические неравенства
Логарифмические неравенства Движение
Движение Двоичная арифметика
Двоичная арифметика Дифференциальные уравнения
Дифференциальные уравнения Виды и особенности нелинейных систем
Виды и особенности нелинейных систем Пирамида
Пирамида Деление обыкновенных дробей
Деление обыкновенных дробей Основные тригонометрические тождества. Преобразование тригонометрических выражений
Основные тригонометрические тождества. Преобразование тригонометрических выражений Условия с логическими связками. Задачи
Условия с логическими связками. Задачи Презентация на тему Площадь многоугольников
Презентация на тему Площадь многоугольников  Уравнение и его корни
Уравнение и его корни Математическая разминка (4 класс)
Математическая разминка (4 класс) Виды углов
Виды углов Таблицы и диаграммы
Таблицы и диаграммы Метод Лагранжа решения ЛНДУ
Метод Лагранжа решения ЛНДУ Тригонометрические функции тангенс и котангенс
Тригонометрические функции тангенс и котангенс Деление многозначного числа на трёхзначное. Решение задачи на нахождение времени совместной работы. 4 класс
Деление многозначного числа на трёхзначное. Решение задачи на нахождение времени совместной работы. 4 класс Перпендикуляр. Определение
Перпендикуляр. Определение Треугольники в окружающем мире
Треугольники в окружающем мире Пифагория. Геометрия в клетках. Геймификация обучения
Пифагория. Геометрия в клетках. Геймификация обучения Решение задач на одновременное встречное движение
Решение задач на одновременное встречное движение Поверхностные интегралы первого рода
Поверхностные интегралы первого рода Формальные логические теории
Формальные логические теории Уравнение касательной к графику функции
Уравнение касательной к графику функции Кроссворд Площади фигур
Кроссворд Площади фигур Презентация на тему Функция у=х^2, её свойства и график
Презентация на тему Функция у=х^2, её свойства и график  Презентация на тему Умножение и деление положительных и отрицательных чисел
Презентация на тему Умножение и деление положительных и отрицательных чисел  Свойство углов при основании равнобедренного треугольника
Свойство углов при основании равнобедренного треугольника