Содержание
- 2. Цель: 8.4.2.3 использовать квадратичную функцию для решения прикладных задач;
- 3. Актуализация знаний. 1.Какая функция называется квадратичной? у = ах² + вх + с, где а, в,
- 4. 2. Из приведенных примеров укажите те функции, которые являются квадратичными. А) у = 5х+1; Б) у
- 5. Б) у = 3х²-1; В) у = -2х²+х+3; Д) у = 4х²; Е) у = -3х²+2х
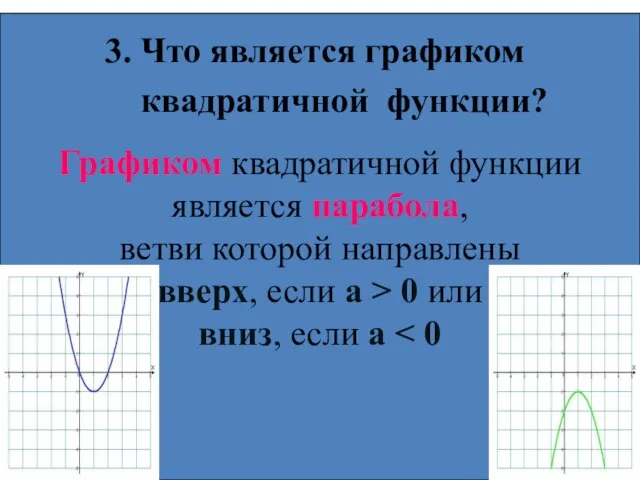
- 6. Графиком квадратичной функции является парабола, ветви которой направлены вверх, если а > 0 или вниз, если
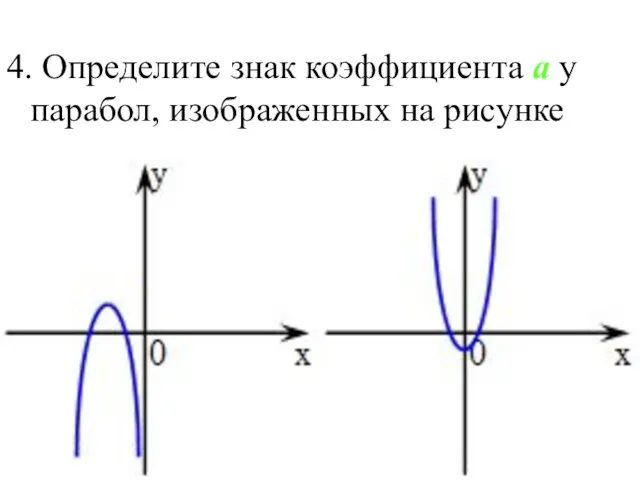
- 7. 4. Определите знак коэффициента a у парабол, изображенных на рисунке
- 8. 5. Как найти координаты вершины параболы?
- 9. Если квадратичная функция представлена в виде у = ах² + вх + с, то координаты вершины
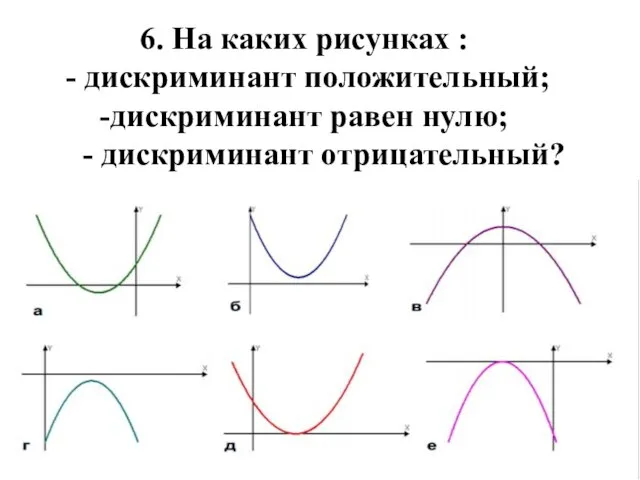
- 10. 6. На каких рисунках : - дискриминант положительный; -дискриминант равен нулю; - дискриминант отрицательный?
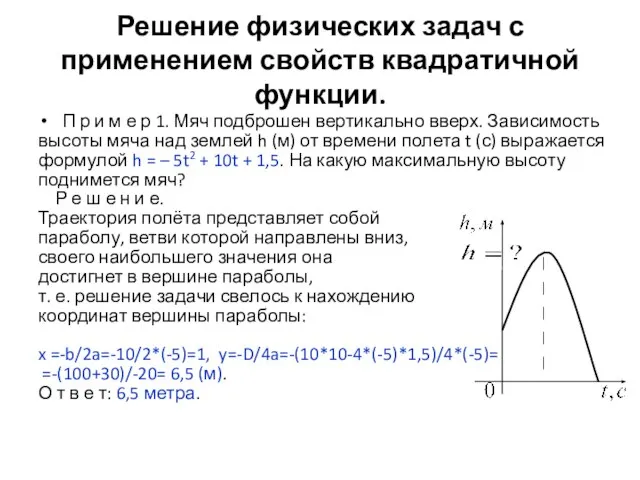
- 11. Решение физических задач с применением свойств квадратичной функции. П р и м е р 1. Мяч
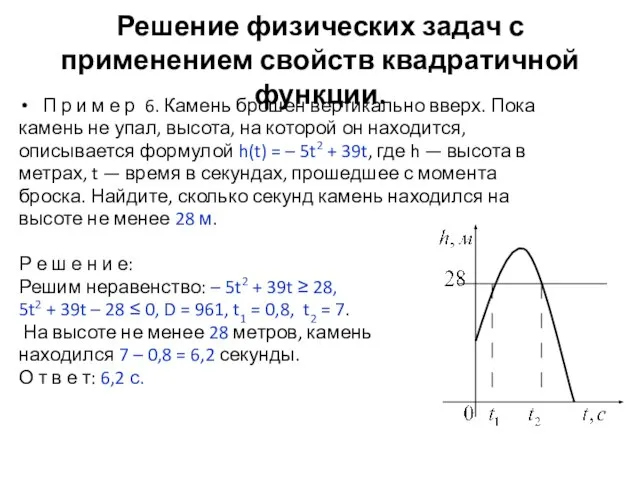
- 13. Решение физических задач с применением свойств квадратичной функции. П р и м е р 6. Камень
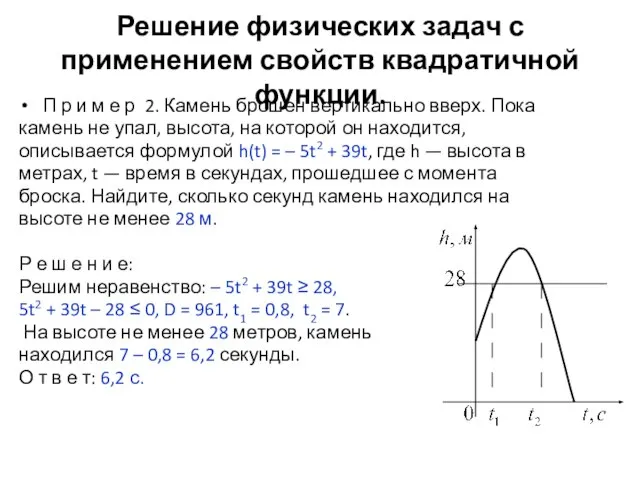
- 14. Решение физических задач с применением свойств квадратичной функции. П р и м е р 2. Камень
- 15. Задание для закрепления Страница 124 № 14.41 Урок в онлайн-мектеп
- 16. Молодцы !!!
- 17. Рефлексия. Мы стали друзьями, мы стали умнее, Богаче на целый волшебный урок! Нас знания делают выше,
- 19. Скачать презентацию



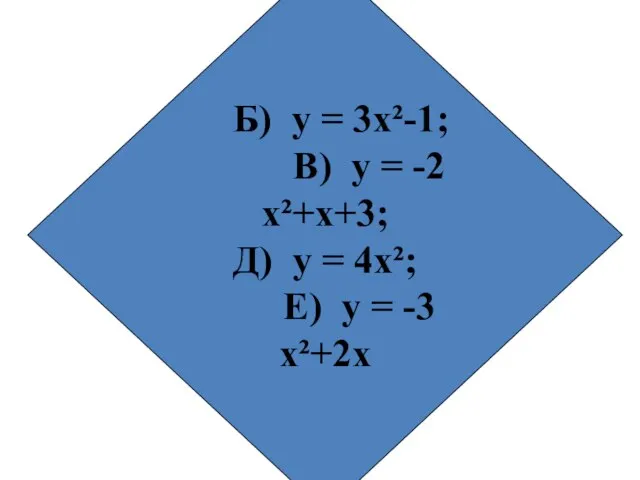






 Случаи вычитания 11 -
Случаи вычитания 11 - Статистические графики
Статистические графики математика гр 32 парність-2.docx
математика гр 32 парність-2.docx Число та цифра 6
Число та цифра 6 Конус. Виды конусов. Конусы в нашей жизни
Конус. Виды конусов. Конусы в нашей жизни Сечения в многогранниках
Сечения в многогранниках Уравнение линии на плоскости. Уравнение фигуры. Уравнение окружности
Уравнение линии на плоскости. Уравнение фигуры. Уравнение окружности Решение задач с помощью уравнений
Решение задач с помощью уравнений Решение задач на движение
Решение задач на движение Понятие спирали
Понятие спирали Геометрические построения
Геометрические построения Элементы теории вероятностей
Элементы теории вероятностей Проценты
Проценты Математические ребусы
Математические ребусы Площади. ОГЭ
Площади. ОГЭ Средняя линия треугольника (8 класс)
Средняя линия треугольника (8 класс) Текстовые задачи на движение по прямой
Текстовые задачи на движение по прямой Основное свойство дроби
Основное свойство дроби Две задачи на дроби
Две задачи на дроби Статистические гипотезы
Статистические гипотезы Собираем ягоды. Математика 1 класс. Итоговое повторение. Тренажёр
Собираем ягоды. Математика 1 класс. Итоговое повторение. Тренажёр Конструктивные объекты
Конструктивные объекты Математика: психология и нейронауки. Чем нейробиология и когнитивная психология могут помочь учителю математики?
Математика: психология и нейронауки. Чем нейробиология и когнитивная психология могут помочь учителю математики? Презентация по математике "Что такое понятие" -
Презентация по математике "Что такое понятие" -  Параллельность плоскостей
Параллельность плоскостей Экономический биатлон. “Экономика и математика”. Финал
Экономический биатлон. “Экономика и математика”. Финал Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними
Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними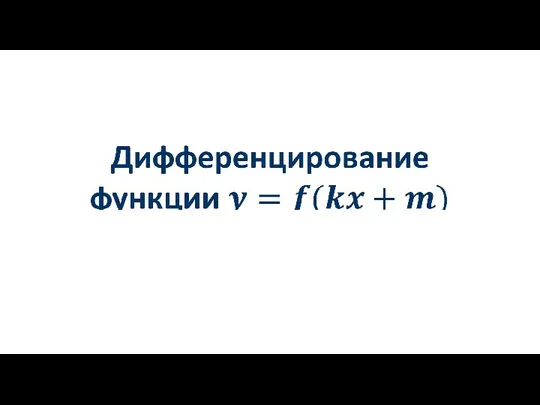 Дифференцирование функции y=f(kx+m)
Дифференцирование функции y=f(kx+m)