Содержание
- 2. Это изображение— фрагмент построения гомеоморфизма в окрестности цепочки седловых связок путём сведения к теореме из книги
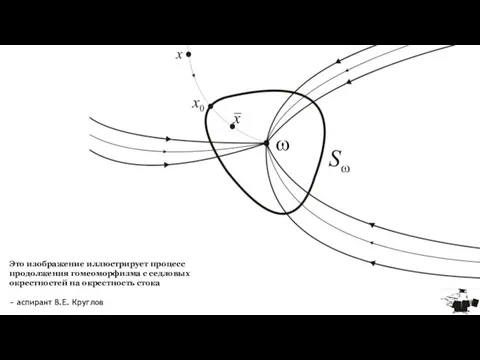
- 3. Это изображение иллюстрирует процесс продолжения гомеоморфизма с седловых окрестностей на окрестность стока ~ аспирант В.Е. Круглов
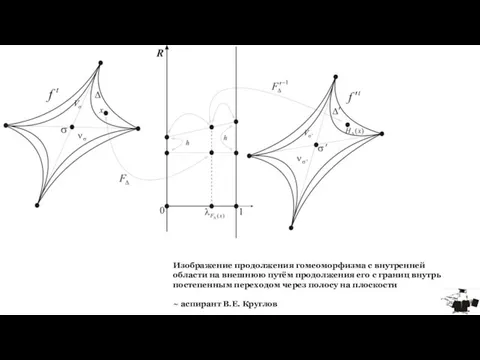
- 4. Изображение продолжения гомеоморфизма с внутренней области на внешнюю путём продолжения его с границ внутрь постепенным переходом
- 5. Аттрактор, принадлежащий к классу однородно гиперболических аттракторов Такие аттракторы составляются исключительно из траекторий седлового типа, причем
- 6. На изображении показано, как эволюционирует некоторая начальная область при последовательных итерациях отображения гиперболического (а), параболического (б)
- 7. Система Розенцвейга-Макартура Математическая модель, описывающая колебания численности цепочки трех популяций: жертвы, хищника и суперхищника (например, планктон
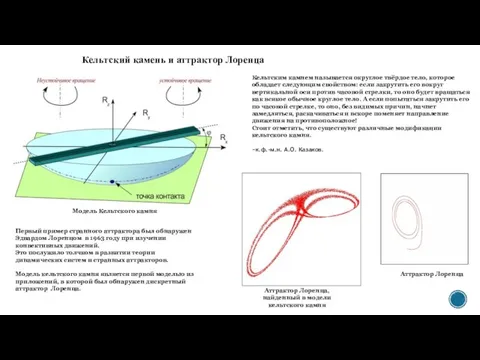
- 8. Кельтский камень и аттрактор Лоренца Кельтским камнем называется округлое твёрдое тело, которое обладает следующим свойством: если
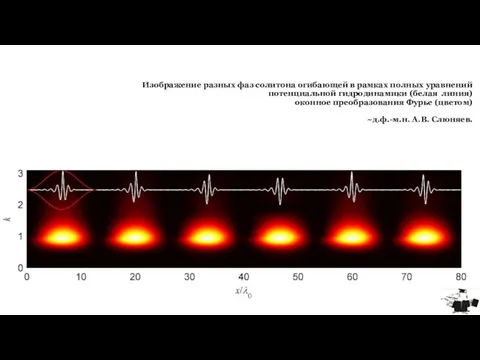
- 9. Изображение разных фаз солитона огибающей в рамках полных уравнений потенциальной гидродинамики (белая линия) оконное преобразования Фурье
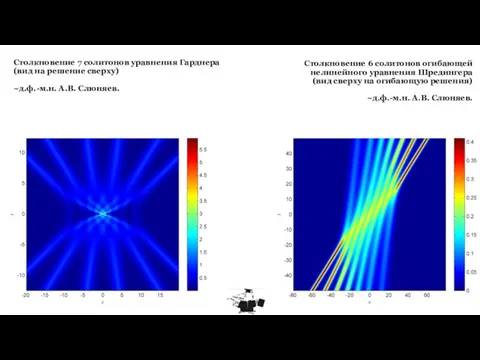
- 10. Столкновение 6 солитонов огибающей нелинейного уравнения Шредингера (вид сверху на огибающую решения) ~д.ф.-м.н. А.В. Слюняев. Столкновение
- 11. Фото пирамидальной волны и реконструкция аналитического решения, моделирующего возникновение аномально высокой волны на поверхности моря (бризер
- 12. Изображение ручки поверхности, которая является топологическим дефектом компьютерной модели На исходном объекте ее нет, а здесь
- 13. Изображение разных этапов работы алгоритма построения базиса группы одномерных гомологий триангулированной поверхности в программном комплексе TSL
- 14. Изображение процесса работы алгоритма поиска базисных 1-циклов на модели Ufo ~ д.ф.-м.н. Е.И. Яковлев.
- 15. Изображение Процесса работы алгоритма поиска базисных 2-циклов на модели Ufo ~ д.ф.-м.н. Е.И. Яковлев.
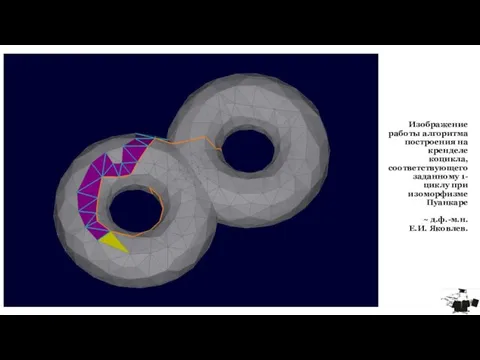
- 16. Изображение работы алгоритма построения на кренделе коцикла, соответствующего заданному 1-циклу при изоморфизме Пуанкаре ~ д.ф.-м.н. Е.И.
- 17. ИНТЕРЕСУЕТЕСЬ МАТЕМАТИКОЙ? Тогда ждем Вас на регулярных семинарах кафедры фундаментальной математики: Каждый вторник в 14:00 (Топологические
- 19. Скачать презентацию










 Матрицы и определители. Основные понятия и определения. Понятие матрицы
Матрицы и определители. Основные понятия и определения. Понятие матрицы Брейн-ринг. Геометрия
Брейн-ринг. Геометрия Геометричекие тела
Геометричекие тела Окружность. 7 класс
Окружность. 7 класс Сложение и вычитание векторов
Сложение и вычитание векторов Тригонометрия. Базовые тригонометрические функции синус, косинус
Тригонометрия. Базовые тригонометрические функции синус, косинус Вариационный ряд. Группировка данных при качественной и количественной вариациях
Вариационный ряд. Группировка данных при качественной и количественной вариациях Преобразования систем координат
Преобразования систем координат Цена, количество, стоимость
Цена, количество, стоимость Сложение и вычитание 4
Сложение и вычитание 4 Фрагмент урока по методике преподавания математики
Фрагмент урока по методике преподавания математики Презентация на тему Функция у=х^3 и её график
Презентация на тему Функция у=х^3 и её график  Решение задач по стереометрии
Решение задач по стереометрии Задачи на дроби
Задачи на дроби Час занимательной математики. 5 класс
Час занимательной математики. 5 класс Перпендикулярность плоскостей. 10 класс
Перпендикулярность плоскостей. 10 класс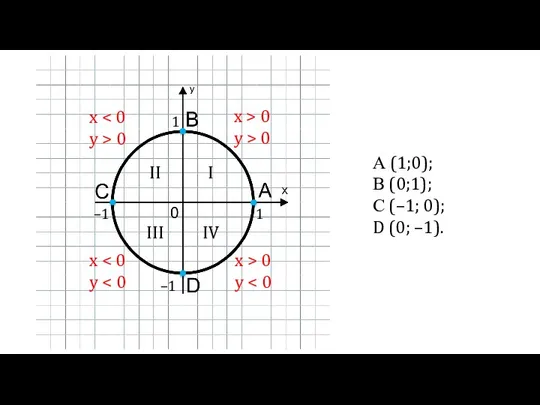 Числовая окружность на координатной плоскости
Числовая окружность на координатной плоскости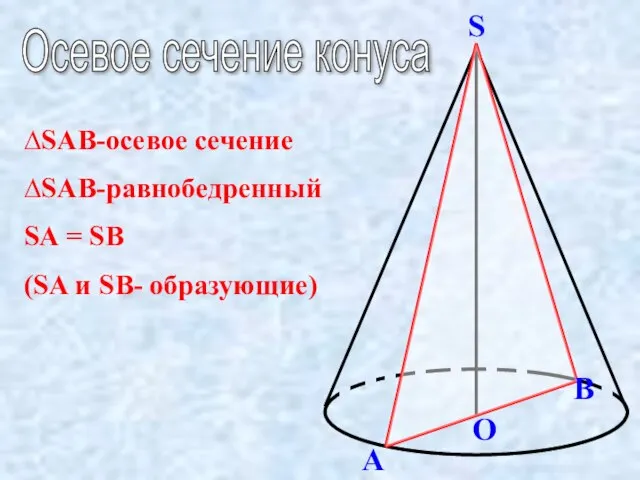 Осевое сечение конуса и цилиндра
Осевое сечение конуса и цилиндра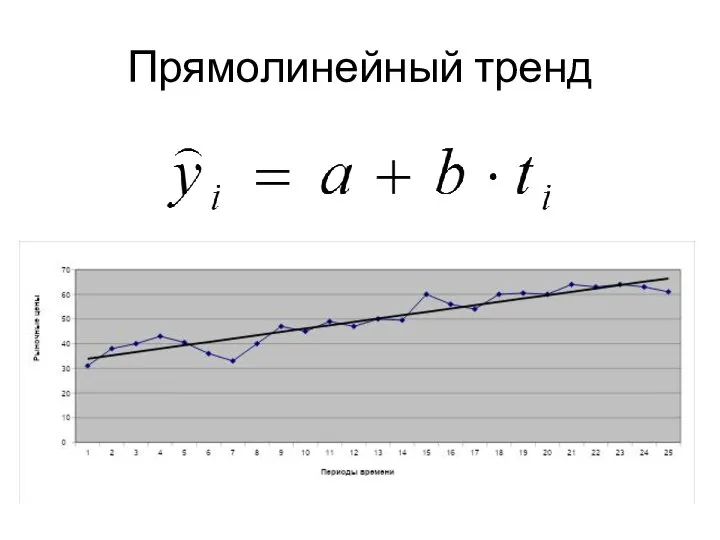 Прямолинейный тренд
Прямолинейный тренд Предел функции в точке и на бесконечности
Предел функции в точке и на бесконечности Математический магазин
Математический магазин Презентация на тему Площадь многоугольников
Презентация на тему Площадь многоугольников 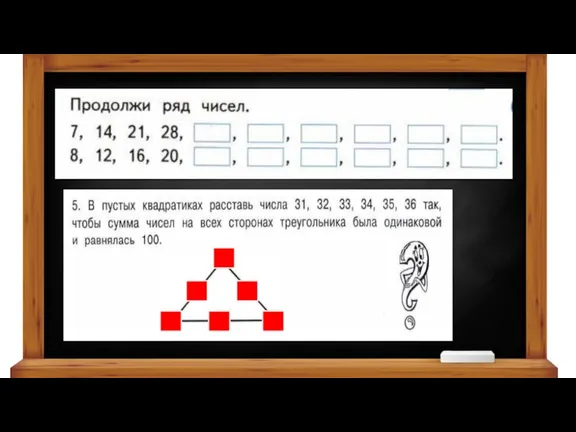 Математика. Закрепление
Математика. Закрепление Множества точек на координатной плоскости, расстояние между точками координатной прямой
Множества точек на координатной плоскости, расстояние между точками координатной прямой Площадь круга и секторов
Площадь круга и секторов Геометрическая прогрессия. 9 класс
Геометрическая прогрессия. 9 класс Многогранники. Решение задач
Многогранники. Решение задач Степень числа с натуральным показателем
Степень числа с натуральным показателем