32046

зміст
Перетворення симетрії відносно осі х
Перетворення симетрії відносно осі у
Паралельне перенесення вздовж осі х
Паралельне перенесення вздовж осі у
Стиск і розтяг вздовж осі Ох
Стиск і розтяг вздовж осі Оу
Побудова графіка функції y=|f(x)| та y=f(|x|)
Побудова графіка оберненої функції
Тестові завдання

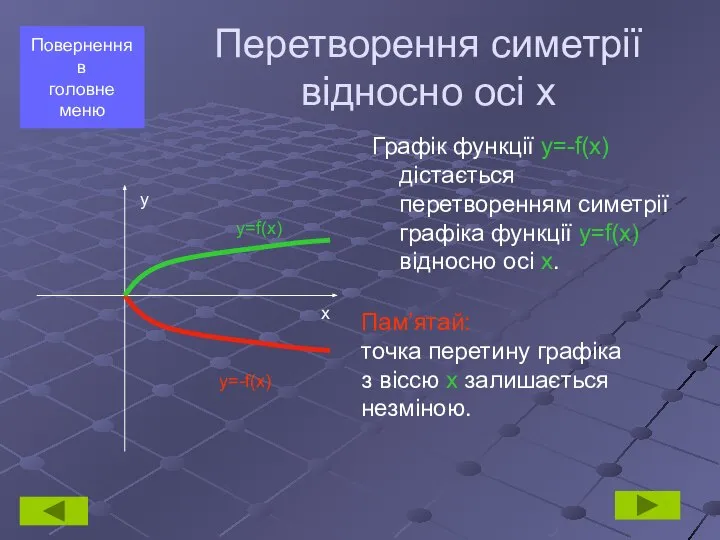
Перетворення симетрії відносно осі х
Графік функції y=-f(x) дістається перетворенням симетрії графіка функції y=f(x) відносно осі х.
Повернення
в
головне
меню
y=-f(x)
y=f(x)
х
у
Пам’ятай:
точка перетину графіка з віссю х залишається незміною.

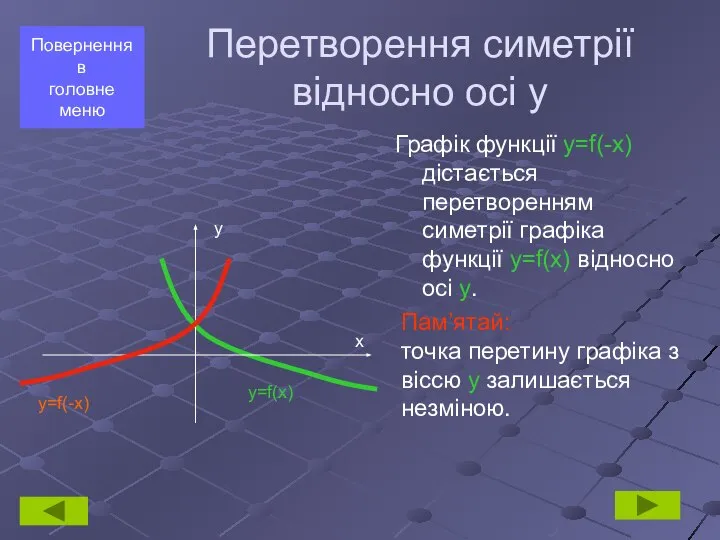
Перетворення симетрії відносно осі у
Графік функції y=f(-x) дістається перетворенням симетрії графіка функції y=f(x) відносно осі у.
Повернення
в
головне
меню
Пам’ятай:
точка перетину графіка з віссю у залишається незміною.
у
х
y=f(-x)
y=f(x)

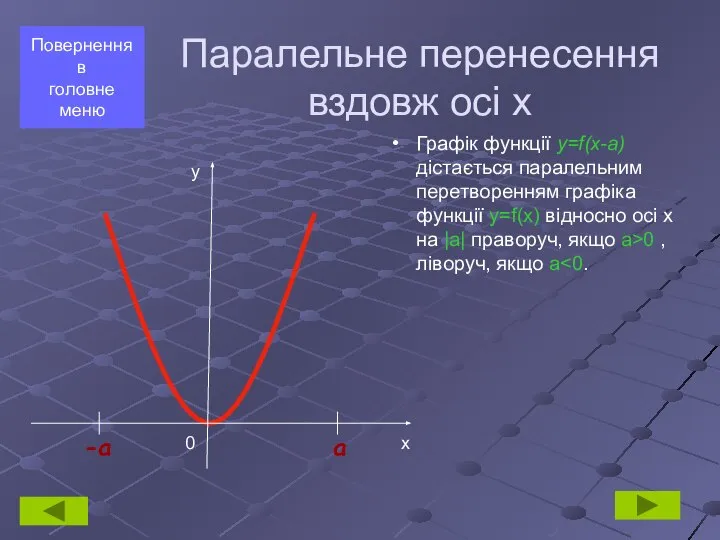
Графік функції y=f(x-а) дістається паралельним перетворенням графіка функції y=f(x) відносно осі х на |a| праворуч, якщо а>0 , ліворуч, якщо a<0.
Повернення
в
головне
меню
Паралельне перенесення вздовж осі х
0
у
х
a
-a

Графік функції y=f(x)+b дістається паралельним перетворенням графіка функції y=f(x) відносно осі у на |b| вгору, якщо b>0 і вниз, якщо b<0
Повернення
в
головне
меню
b
-b
0
y=f(x)+b
y=f(x)-b
y=f(x)
у
х
Паралельне перенесення вздовж осі у

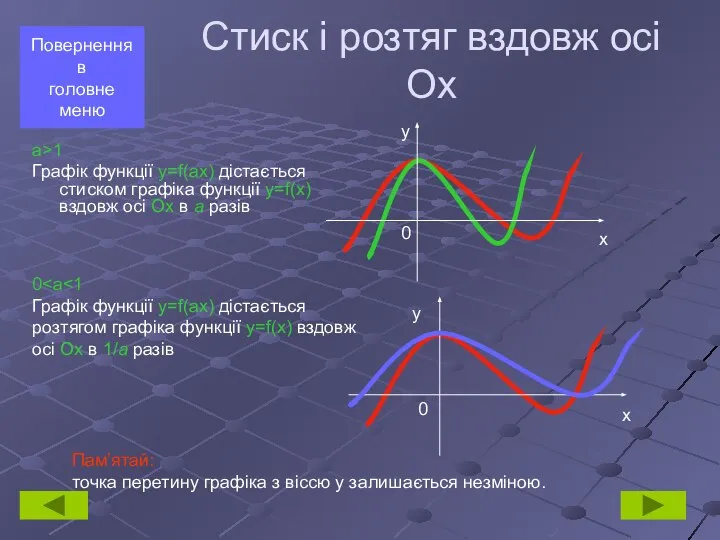
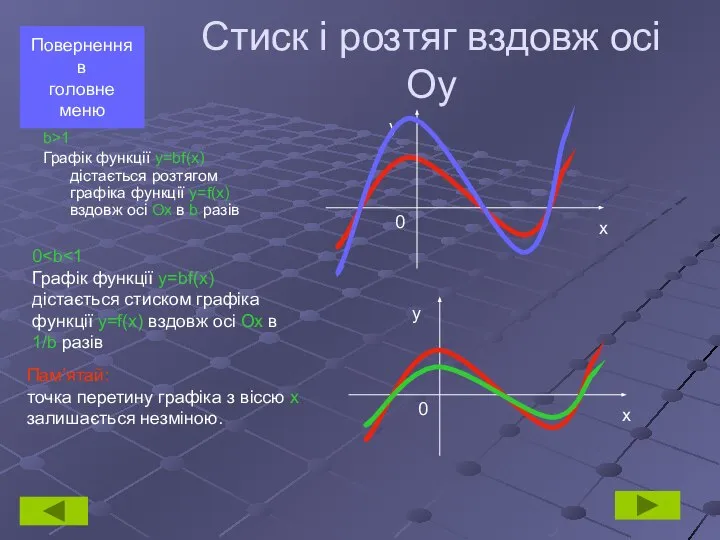
a>1
Графік функції y=f(ax) дістається стиском графіка функції y=f(x) вздовж осі Ох в а разів
Повернення
в
головне
меню
0
у
х
0
у
х
0
Графік функції y=f(ax) дістається розтягом графіка функції y=f(x) вздовж осі Ох в 1/а разів
Пам’ятай:
точка перетину графіка з віссю у залишається незміною.
Стиск і розтяг вздовж осі Ох

b>1
Графік функції y=bf(x) дістається розтягом графіка функції y=f(x) вздовж осі Ох в b разів
Повернення
в
головне
меню
у
х
0
у
х
0
0
Графік функції y=bf(x) дістається стиском графіка функції y=f(x) вздовж осі Ох в 1/b разів
Пам’ятай:
точка перетину графіка з віссю x залишається незміною.
Стиск і розтяг вздовж осі Оу

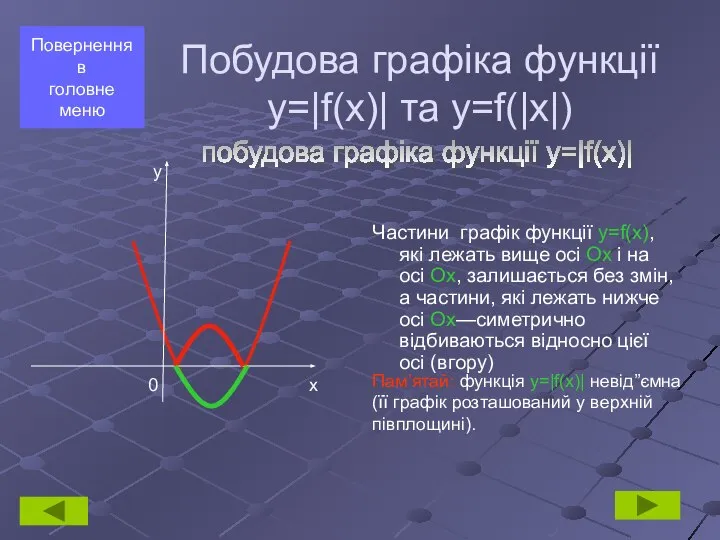
Частини графік функції y=f(x), які лежать вище осі Ох і на осі Ох, залишається без змін, а частини, які лежать нижче осі Ох—симетрично відбиваються відносно цієї осі (вгору)
Повернення
в
головне
меню
побудова графіка функції y=|f(x)|
Побудова графіка функції y=|f(x)| та y=f(|x|)
Пам’ятай: функція y=|f(x)| невід”ємна (її графік розташований у верхній півплощині).
0
у
х

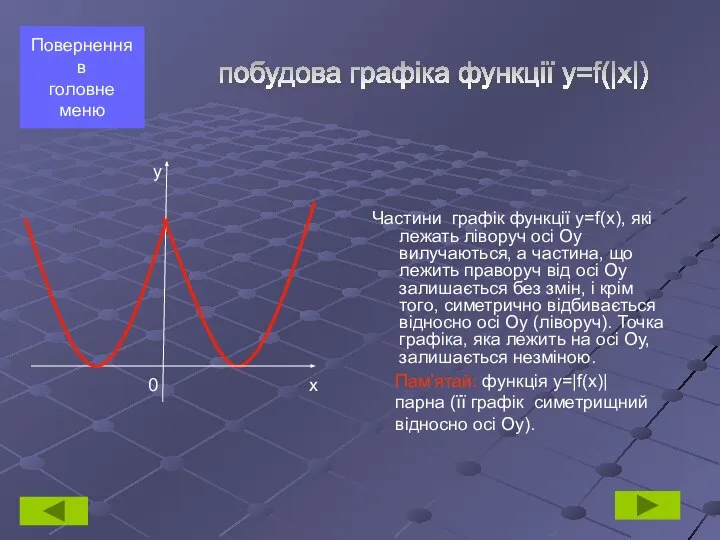
Частини графік функції y=f(x), які лежать ліворуч осі Оу вилучаються, а частина, що лежить праворуч від осі Оу залишається без змін, і крім того, симетрично відбивається відносно осі Оу (ліворуч). Точка графіка, яка лежить на осі Оу, залишається незміною.
Повернення
в
головне
меню
побудова графіка функції y=f(|x|)
Пам’ятай: функція y=|f(x)| парна (її графік симетрищний відносно осі Оу).
0
у
х

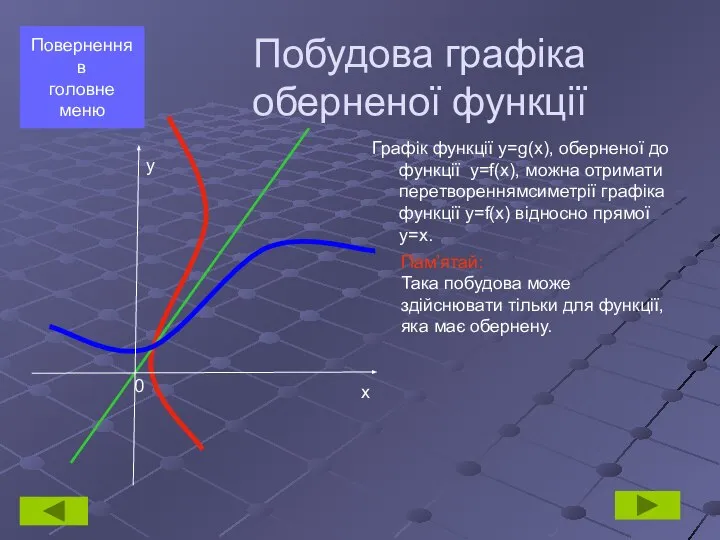
Графік функції y=g(x), оберненої до функції y=f(x), можна отримати перетвореннямсиметрії графіка функції y=f(x) відносно прямої у=х.
Повернення
в
головне
меню
Побудова графіка оберненої функції
0
у
х
Пам’ятай:
Така побудова може здійснювати тільки для функції, яка має обернену.

Тестові завдання
Start
Повернення
в
головне
меню

Як з графіка функції у=2х
утворити графік функції у=-2х.
перетворенням симетрії графіка функції
паралельним перетворенням графіка функції
дістається стиском графіка функції

Як можна побудувати графік функції
Графік функції дістається паралельним перетворенням графіка функції відносно осі Ох в ліво
на 1, після чого паралельним перетворенням утворений графік функції переносимо відносно осі Оу вгору на 3.
Графік функції дістається паралельним
перетворенням графіка функції відносно осі Оу вгору на 3,
і потім паралельним перетворенням відносно осі Ох вліво на 1
Графік функції дістається паралельним перетворенням графіка функції відносно осі Ох в ліво
на 3, після чого теж паралельним перетворенням відносно осі Оу вгору на 1.

Напишіть функцію даного графіка

Дізнайся
результат