Уравнением с параметром. Неизвестные величины

Уравнением с параметром а называют уравнение вида f(x, a) = 0, которое надо решить относительно х и в котором буквой а обозначено произвольное действительное число.

Решить уравнение с параметром – значит для каждого значения параметра найти множество всех корней данного уравнения или доказать, что корней нет.

Пример 1. Решить уравнение ax = 1.
Решение.
1. если a ≠ 0:
2. если a = 0:
0 · x = 1 – не имеет решений;

Пример 2. Решить уравнение a2x – 1 = x + a.
Решение.
a2x – 1 = x + a ;
a2x – x = a + 1;
x(a2 – 1) = a + 1;
1. если a2 – 1 ≠ 0, то есть a ≠ ±1:
2. если a = 1, то есть 0 · x = 2:
уравнение не имеет решений;
3. если a = –1, то есть 0 · x = 0:

Решение.
ОДЗ:
х – 4 ≠ 0;
х ≠ 4;
х – 2а = 0;
х = 2а;
х ≠ 4:
2а ≠ 4;
а ≠ 2;
а ≠ 2: x = 2a;
a = 2: уравнение не имеет решений;
Ответ: если а ≠ 2, то уравнение имеет единственное решение x = 2a;
если a = 2, то уравнение не имеет решений.

Пример 4. Решить уравнение |x – a| = 2.
Решение.
x1 = a + 2, x2 = a – 2;
Ответ: x1 = a + 2, x2 = a – 2.

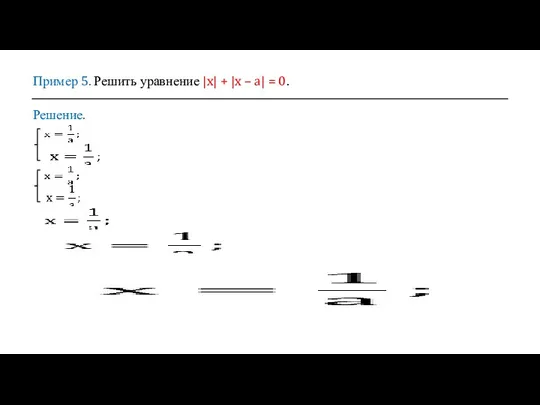
Пример 5. Решить уравнение |x| + |x – a| = 0.
Решение.

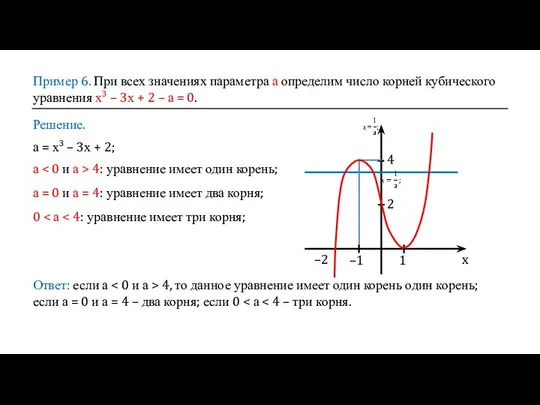
Пример 6. При всех значениях параметра а определим число корней кубического уравнения х3 – 3х + 2 – а = 0.
Решение.
а = х3 – 3х + 2;
–2
–1
1
x
2
4
а < 0 и а > 4: уравнение имеет один корень;
а = 0 и а = 4: уравнение имеет два корня;
0 < а < 4: уравнение имеет три корня;
Ответ: если а < 0 и а > 4, то данное уравнение имеет один корень один корень; если а = 0 и а = 4 – два корня; если 0 < а < 4 – три корня.

Пример 7. Решить уравнение mх2 + 3mх – (m+2) = 0.
Решение.
D = m(13m + 8);
D = m(13m + 8) ≥ 0;