Непрерывность функций

Непрерывность
Определение.
Функция f(x) называется непрерывной , в точке х = а , если соблюдается следующие условия:
При х = а функция f(x) имеет определенное значение b.
При х —› а функция имеет предел, тоже равный b.
При нарушение хотя бы одного из этих условий функция называется разрывной в точке х = а .

Условие непрерывности
Существование равносильно тому,
что существуют равные друг другу левосторонний и правосторонний пределы функции при , равные к тому же и значению функции в точке, то есть

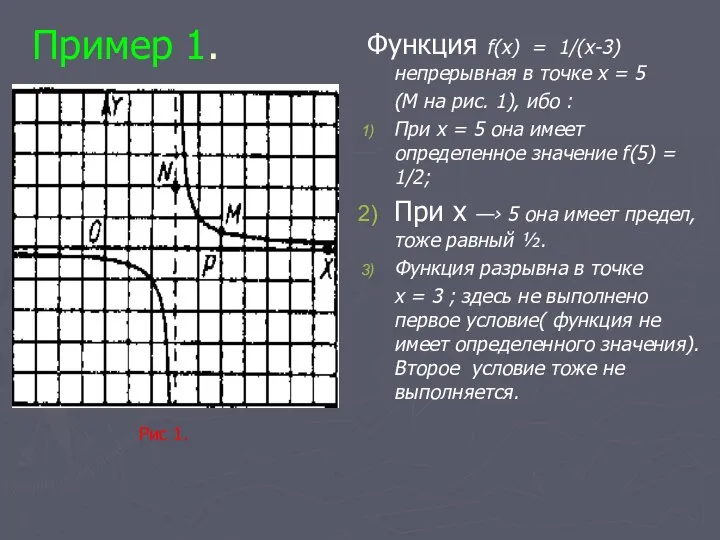
Пример 1.
Функция f(x) = 1/(х-3) непрерывная в точке х = 5
(М на рис. 1), ибо :
При х = 5 она имеет определенное значение f(5) = 1/2;
При х —› 5 она имеет предел, тоже равный ½.
Функция разрывна в точке
х = 3 ; здесь не выполнено первое условие( функция не имеет определенного значения). Второе условие тоже не выполняется.
Рис 1.

Свойство функций, непрерывных в точке.
Свойство 1.
Сумма, разность и произведение двух функций, непрерывных в точке х = а, непрерывны в этой точке. Частное u/U двух функций, непрерывных в точке
х = а, непрерывно , если делитель U не обращается в нуль при х = а.

Свойства 2.
Если функция f(x) непрерывна при некоторой значении х, то приращение функции бесконечно мало при бесконечно малом приращение аргумента.
Пример 2.
Функция f(х) = 1/ (х – 3) непрерывна в точке х = 5, причем f(5) = ½(пример 1).
При х = 5 + ∆х.
Функция получает значение
f(5 + ∆х) = 1/(2 + ∆х).
Приращение функции равно
f(5 + ∆х) – f(5) = - ∆х/ (2(2+ ∆х))
Оно бесконечно мало при бесконечно малом ∆х.

Непрерывность на множестве
Говорят, что функция непрерывна на множестве Х, если она непрерывна в каждой точке этого множества.
Если функция непрерывна в каждой точке отрезка [a, b], то говорят, что она непрерывна на этом отрезке, причем непрерывность в точке а понимается как непрерывность справа, а непрерывность в точке b – как непрерывность слева.

Непрерывность
Теорема. Функция непрерывна в точке тогда и только тогда, когда бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции в этой точке, то есть если

Теоремы о непрерывных функциях
Теорема (о непрерывности сложной функции). Пусть функция
непрерывна в точке , а функция непрерывна в точке . Тогда сложная функция непрерывна в точке

Разрывы функций
Дадим теперь классификацию точек разрыва функций. Возможны следующие случаи.
1.Если существуют и конечны, но не равны друг другу, то точку называют точкой разрыва первого рода. При этом величину называют скачком функции в точке .

Разрывы функций
2.Если в точке , но в точке функция либо не определена, либо , то эта точка является точкой устранимого разрыва. Последнее объясняется тем, что если в этом случае доопределить или видоизменить функцию , положив
,
то получится непрерывная в точке функция.

Разрывы функций
3. Точка разрыва функции, не являющаяся точкой разрыва первого рода или точкой устранимого разрыва, является точкой разрыва второго рода.
Очевидно, что точки разрыва второго рода - это точки, в которых функция стремится к бесконечности. Например, в точке х=1 имеет разрыв 2-го рода.

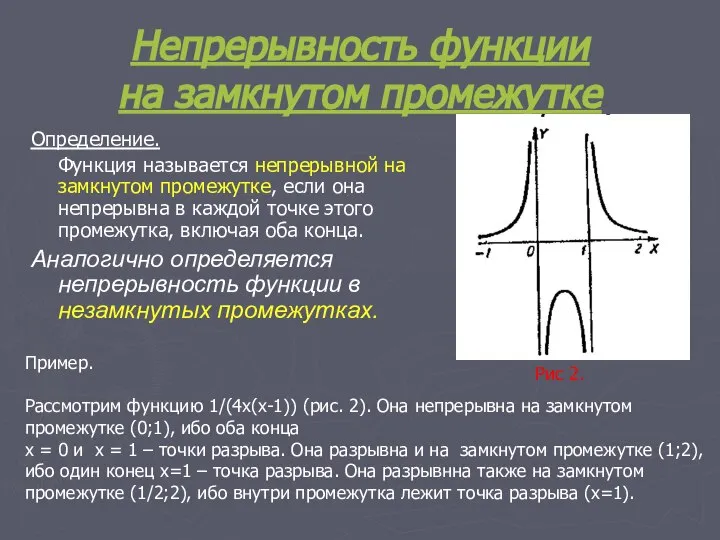
Непрерывность функции
на замкнутом промежутке
Определение.
Функция называется непрерывной на замкнутом промежутке, если она непрерывна в каждой точке этого промежутка, включая оба конца.
Аналогично определяется непрерывность функции в незамкнутых промежутках.
Рис 2.
Пример.
Рассмотрим функцию 1/(4х(х-1)) (рис. 2). Она непрерывна на замкнутом промежутке (0;1), ибо оба конца
х = 0 и х = 1 – точки разрыва. Она разрывна и на замкнутом промежутке (1;2), ибо один конец х=1 – точка разрыва. Она разрывнна также на замкнутом промежутке (1/2;2), ибо внутри промежутка лежит точка разрыва (х=1).

Свойство функций, непрерывных
на замкнутом промежутке
Пусть функция f(х) непрерывна на замкнутом промежутке (a,b).
Тогда она обладает следующими свойствами.
Среди значений, которые функция принимает в точках данного промежутка, имеется самое большое и самое малое.
Замечание 1. Среди значений, которые принимает функция f(х) в точке незамкнутого промежутка (a,b), может не быть самого большого или самого малого.
Так, в незамкнутом промежутке (1,3) функция 2х не обладает ни наименьшим значением, ни наибольшим (она могла бы принять эти значения на концах х=1 и х=3 , но из незамкнутого промежутка концы исключены).

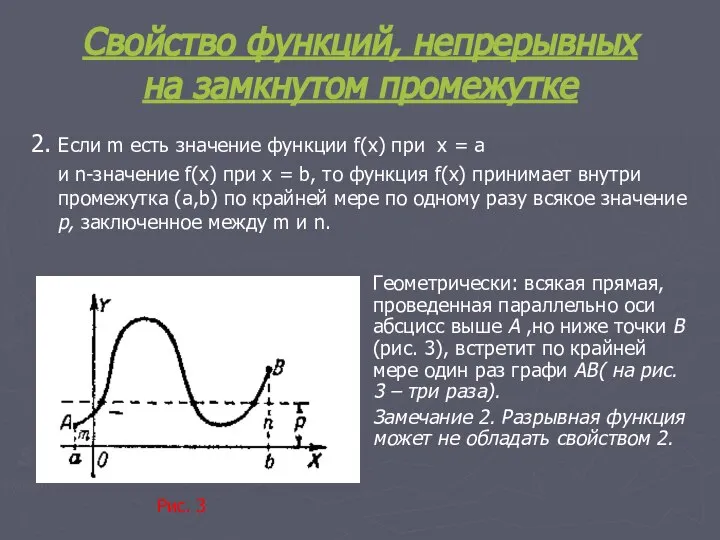
Свойство функций, непрерывных
на замкнутом промежутке
2. Если m есть значение функции f(х) при х = а
и n-значение f(х) при х = b, то функция f(х) принимает внутри промежутка (а,b) по крайней мере по одному разу всякое значение p, заключенное между m и n.
Геометрически: всякая прямая, проведенная параллельно оси абсцисс выше А ,но ниже точки В (рис. 3), встретит по крайней мере один раз графи АВ( на рис. 3 – три раза).
Замечание 2. Разрывная функция может не обладать свойством 2.
Рис. 3

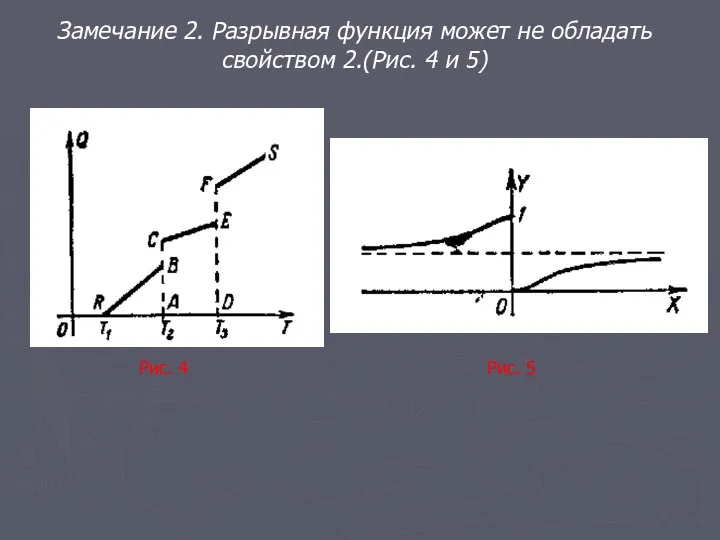
Замечание 2. Разрывная функция может не обладать свойством 2.(Рис. 4 и 5)
Рис. 4
Рис. 5

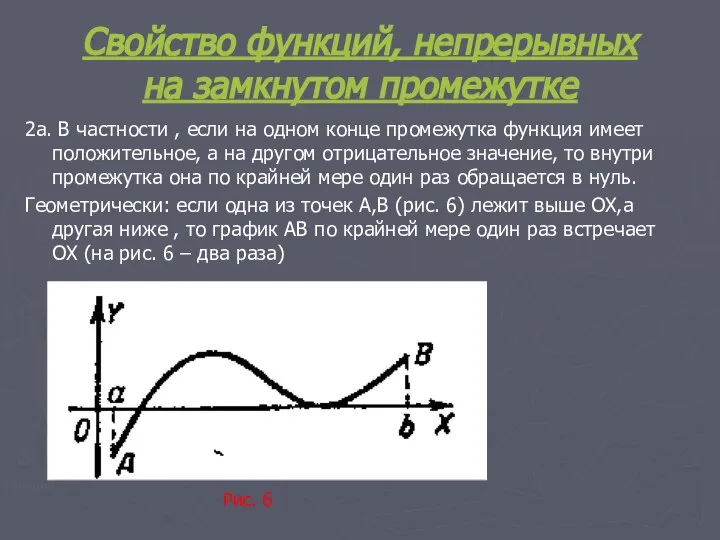
Свойство функций, непрерывных
на замкнутом промежутке
2а. В частности , если на одном конце промежутка функция имеет положительное, а на другом отрицательное значение, то внутри промежутка она по крайней мере один раз обращается в нуль.
Геометрически: если одна из точек А,В (рис. 6) лежит выше ОХ,а другая ниже , то график АВ по крайней мере один раз встречает ОХ (на рис. 6 – два раза)
Рис. 6

Свойство функций, непрерывных
на замкнутом промежутке
3. Если переменные х и х´ изменяются так, что разность х - х´ бесконечно мала, то разность f(x) – f(x´) тоже бесконечно мала.
Замечание 3. Если х´ есть постоянная величина с, то разность f(x) – f(с) является бесконечно малой по свойству 2. В силу свойства 3 при бесконечной малости х - х´ разность f(x) – f(x´) бесконечно мала не только тогда, когда х´ постоянна, но и тогда, когда х´ переменна.
Замечание 4. При непрерывности функции в незамкнутом промежутке свойства 3 может не иметь места. Так, функция 1/х непрерывна в промежутке (0,1),лишенном конца х = 0. Пусть х и х´ изменится так, что х´= 2х и х—›0. Тогда разность х - х´ бесконечно мала, но разность f(x) – f(x´) = 1/х – 1/2х бесконечно велика.

Свойства непрерывных на отрезке функций
Первая теорема Больцано - Коши об обращении функции в нуль. Пусть функция определена и непрерывна на отрезке [a, b] и на концах этого отрезка принимает значения различных знаков, т. е.
Тогда существует точка
такая, что

Свойства непрерывных на отрезке функций
Вторая теорема Больцано-Коши о промежуточном значении функции. Пусть функция определена и непрерывна на отрезке [a, b] и на концах этого отрезка принимает неравные значения . Тогда, каково бы ни было число между числами , найдется точка такая, что

Свойства непрерывных на отрезке функций
Теорема 1 Вейерштрасса.
Если функция определена и непрерывна на отрезке [a,b], то она на этом отрезке ограничена, то есть существуют числа m и М такие, что m М для любого .