3.3. Понятие функции

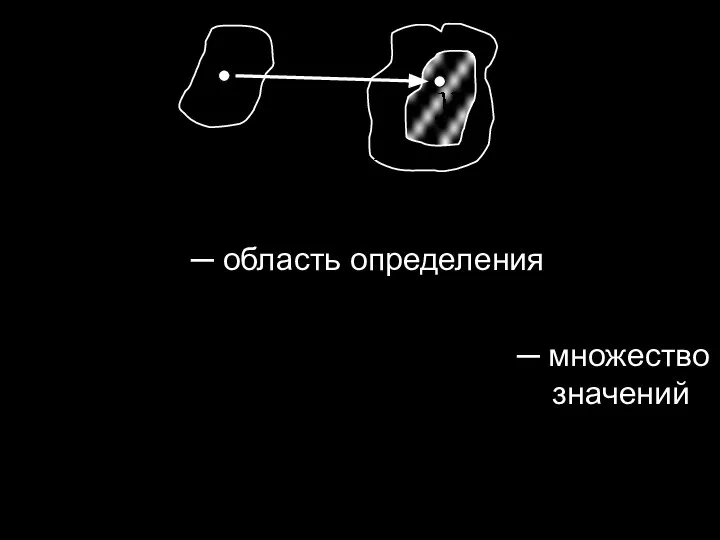
─ область определения
─ множество а значений

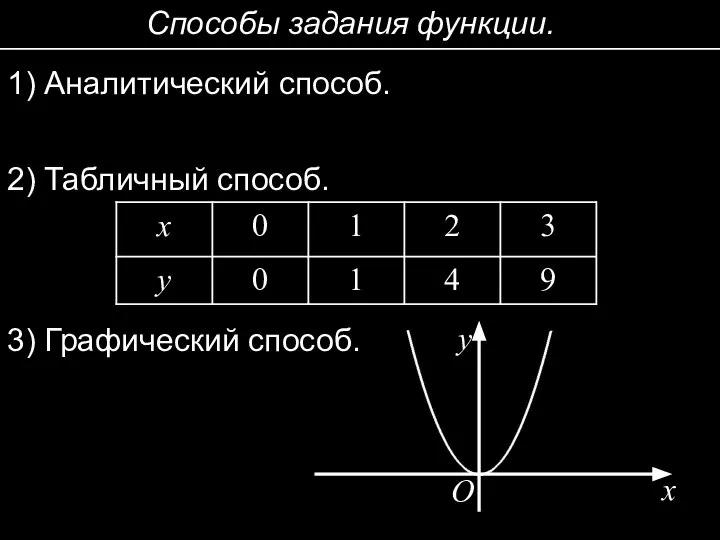
Способы задания функции.
1) Аналитический способ.
2) Табличный способ.
3) Графический способ.
x
y
O

Основные характеристики функций
1) Четность (нечетность).
Функция определенная на множестве D,
Функция определенная на множестве D, называется четной (нечетной),
если выполняются условия:

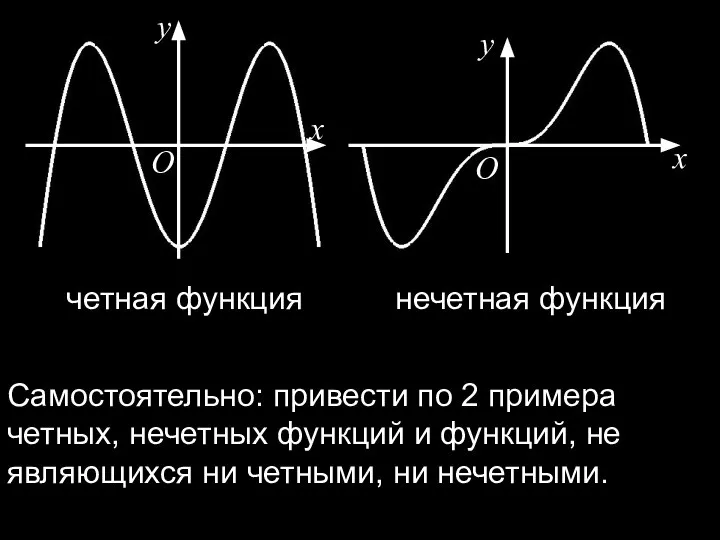
x
y
O
x
y
O
четная функция
нечетная функция
Самостоятельно: привести по 2 примера четных, нечетных функций и функций, не являющихся ни четными, ни нечетными.

2) Монотонность.
Функция определенная на множестве D,
Функция определенная на множестве D, называется строго возрастающей (строго убывающей) на множестве
если
Строго возрастающие
Строго убывающие
Строго монотонные функции

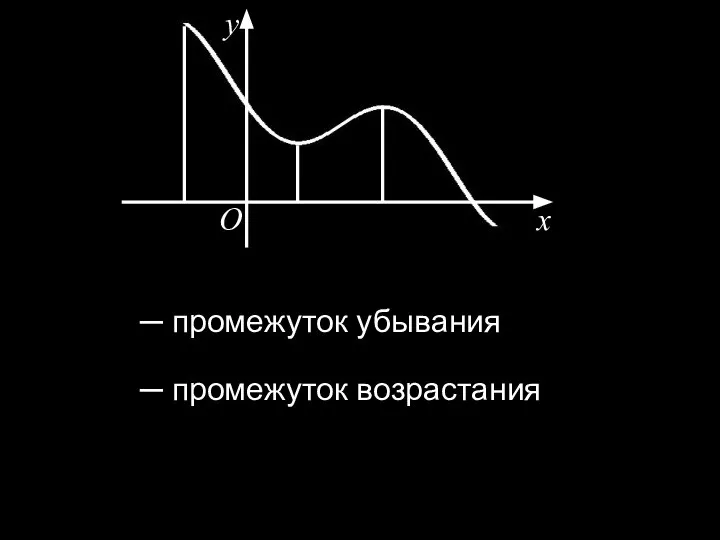
x
y
O
─ промежуток убывания
─ промежуток возрастания

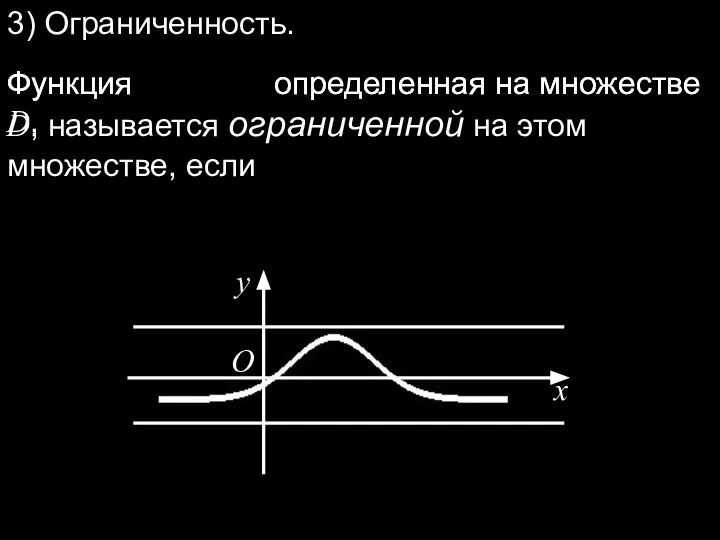
Функция определенная на множестве D,
Функция определенная на множестве D, называется ограниченной на этом множестве, если
3) Ограниченность.
x
y
O

Функция определенная на множестве D,
Функция определенная на множестве D, называется периодической на этом множестве, если
4) Периодичность.
─ период

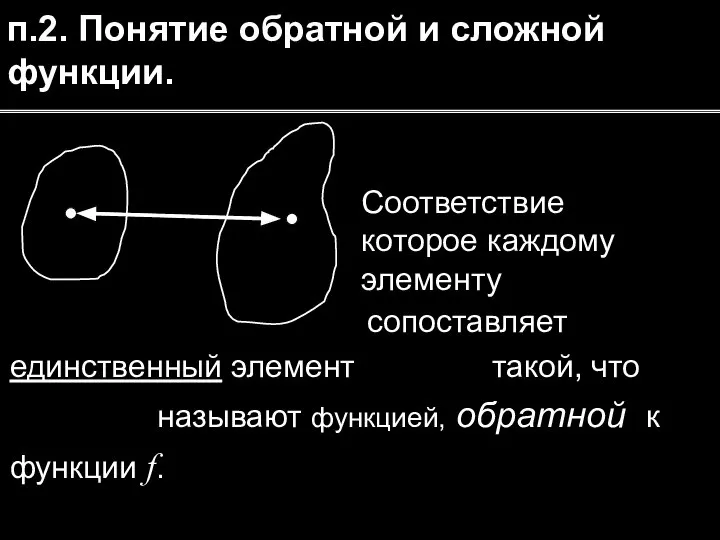
п.2. Понятие обратной и сложной функции.
Соответствие
которое каждому элементу
сопоставляет
единственный элемент
такой, что
называют функцией, обратной к
функции f.

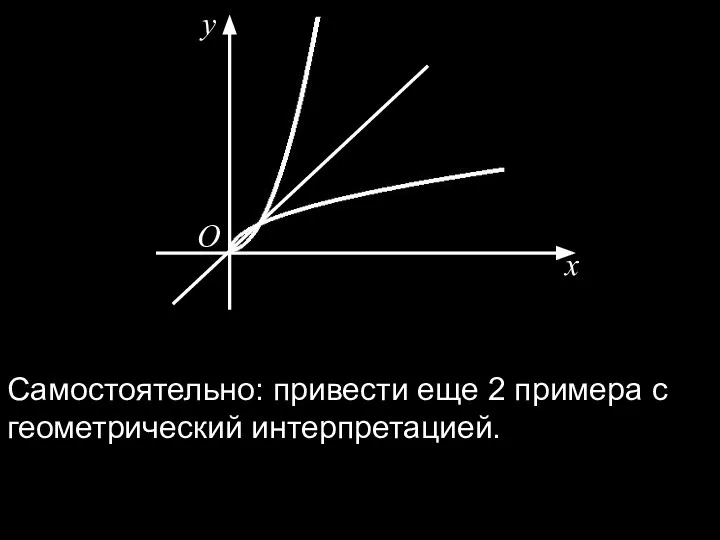
x
y
O
Самостоятельно: привести еще 2 примера с геометрический интерпретацией.

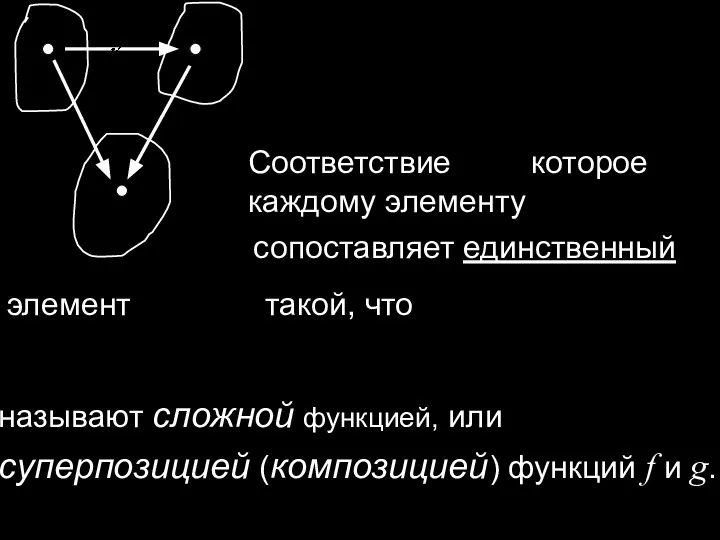
Соответствие которое каждому элементу
сопоставляет единственный
элемент
такой, что
называют сложной функцией, или
суперпозицией (композицией) функций f и g.