Правильные многогранники

Определение многогранника
Многогранник – это часть пространства, ограниченная совокупностью конечного числа плоских многоугольников, соединённых таким образом, что каждая сторона любого многогранника является стороной ровно одного многоугольника. Многоугольники называются гранями, их стороны – рёбрами, а вершины – вершинами.

Многогранник называется правильным, если: 1) он выпуклый; 2) все его грани – равные друг другу правильные многоугольники ; 3) в каждой его вершине сходится одинаковое число ребер; 4) все его двугранные углы равны.
Примером правильного многогранника является куб, тетраэдр
Определение правильного
многогранника

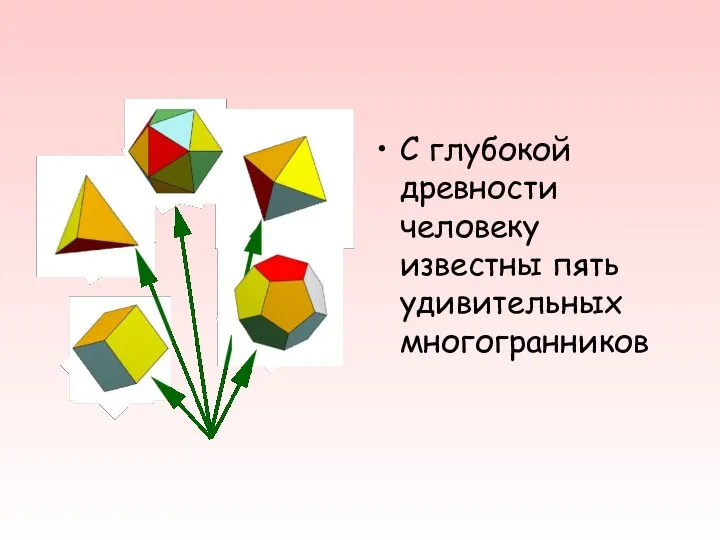
С глубокой древности человеку известны пять удивительных многогранников

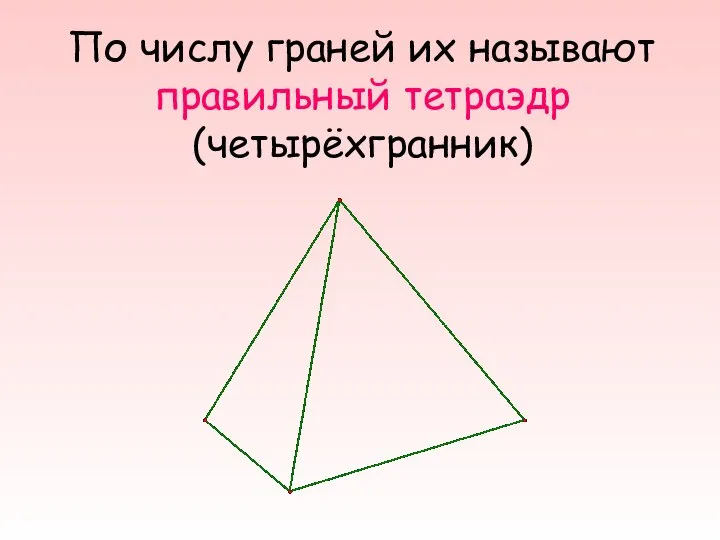
По числу граней их называют правильный тетраэдр (четырёхгранник)

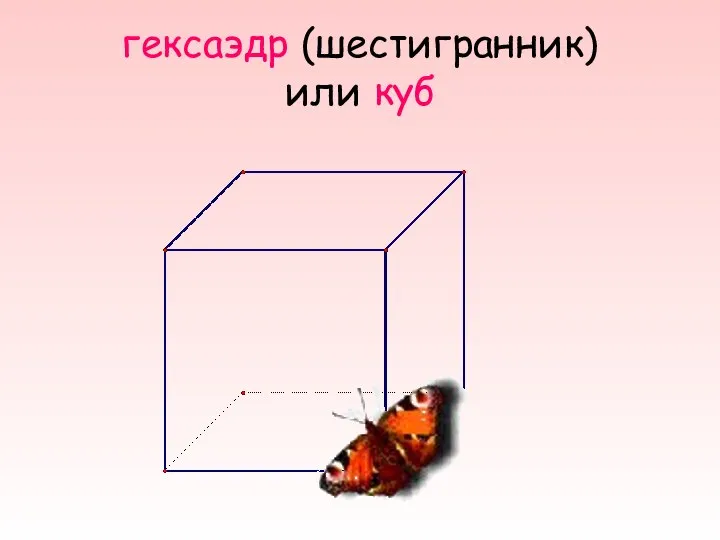
гексаэдр (шестигранник)
или куб

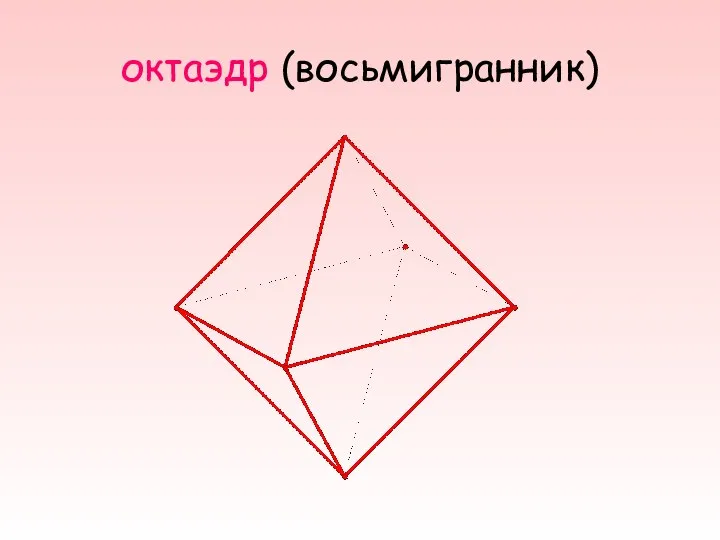
октаэдр (восьмигранник)

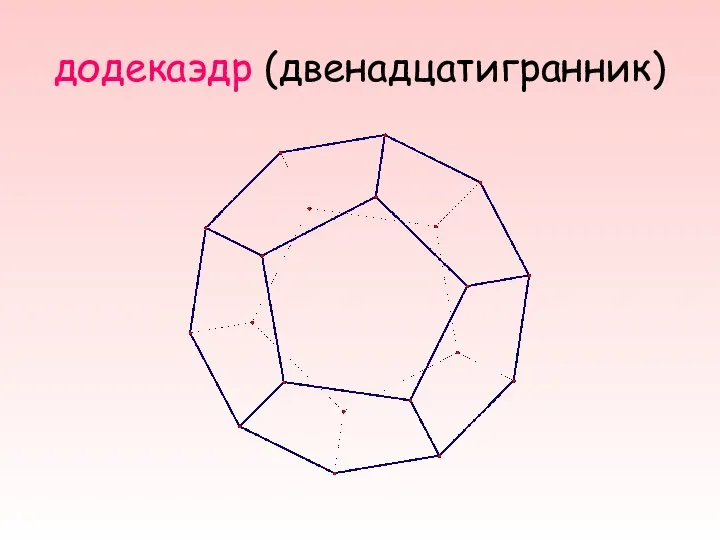
додекаэдр (двенадцатигранник)

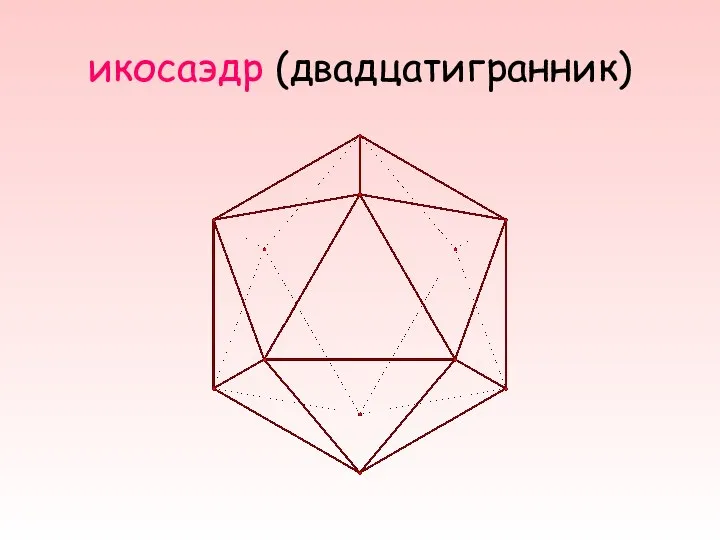
икосаэдр (двадцатигранник)

Свойства этих многогранников изучали ученые и священники, их модели можно было увидеть в работах архитекторов и ювелиров, им приписывались различные магические и целебные свойства

Великий древнегреческий философ Платон, живший в IV – V вв. до нашей эры, считал, что эти тела олицетворяют сущность природы

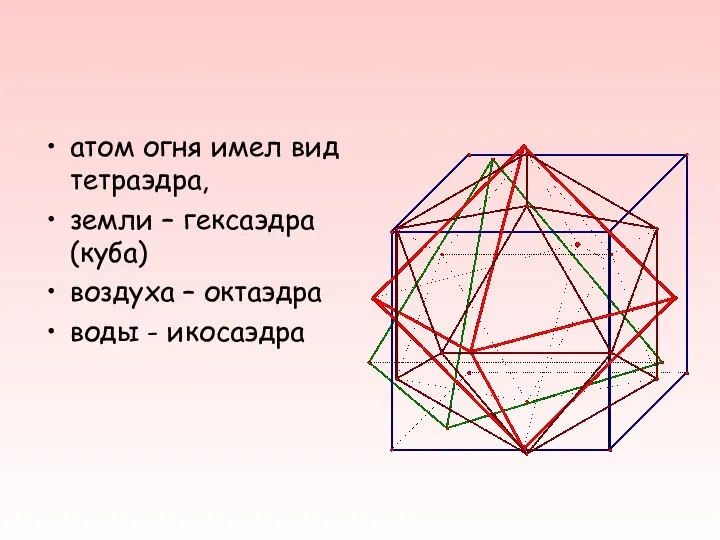
Четыре сущности природы были известны человечеству: огонь, вода, земля и воздух. По мнению Платона, их атомы имели вид правильных многогранников

атом огня имел вид тетраэдра,
земли – гексаэдра (куба)
воздуха – октаэдра
воды - икосаэдра

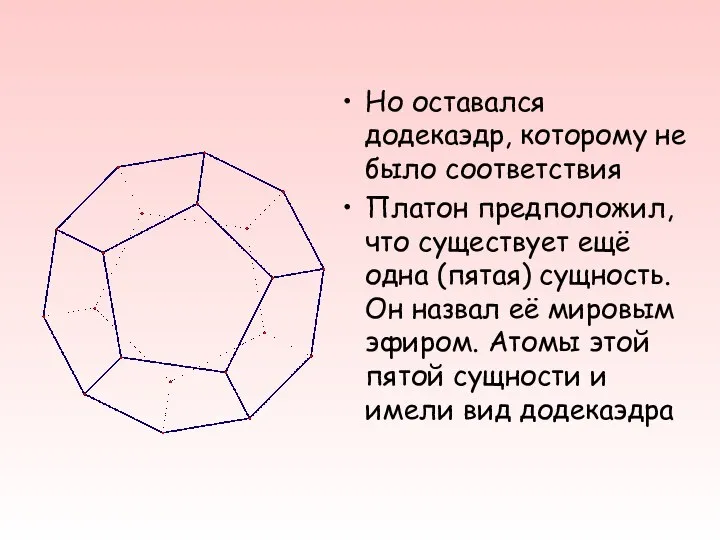
Но оставался додекаэдр, которому не было соответствия
Платон предположил, что существует ещё одна (пятая) сущность. Он назвал её мировым эфиром. Атомы этой пятой сущности и имели вид додекаэдра

Платон и его ученики в своих работах большое внимание уделяли перечисленным многогранникам. Поэтому эти многогранники называют также платоновыми телами

Определение правильного многогранника
Многогранник называется правильным, если все его грани – равные между собой правильные многоугольники, из каждой вершины выходит одинаковое число ребер и все двугранные углы равны

Платоновы тела - трехмерный аналог плоских правильных многоугольников. Однако между двумерным и трехмерным случаями есть важное отличие: существует бесконечно много различных правильных многоугольников, но лишь пять различных правильных многогранников

Доказательство этого факта известно уже более двух тысяч лет; этим доказательством и изучением пяти правильных тел завершаются "Начала" Евклида

Существует лишь пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями

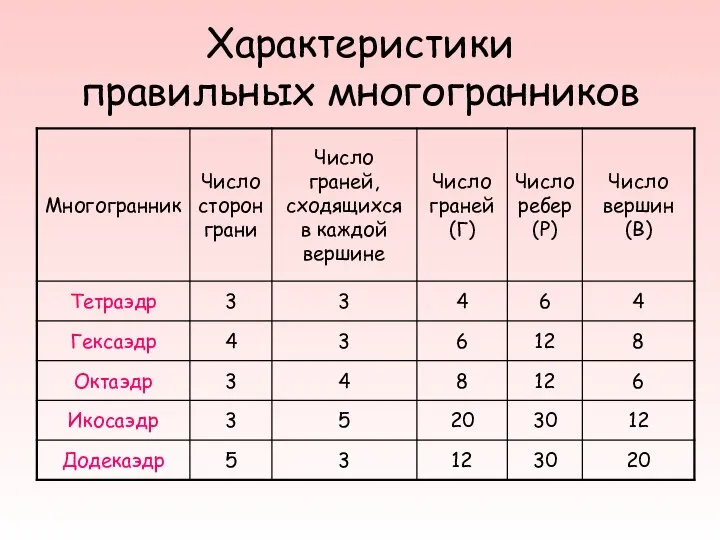
Характеристики
правильных многогранников

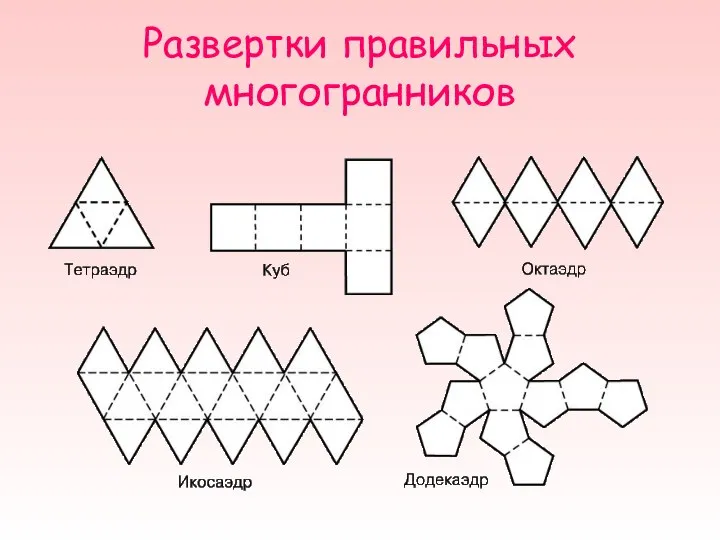
Развертки правильных многогранников

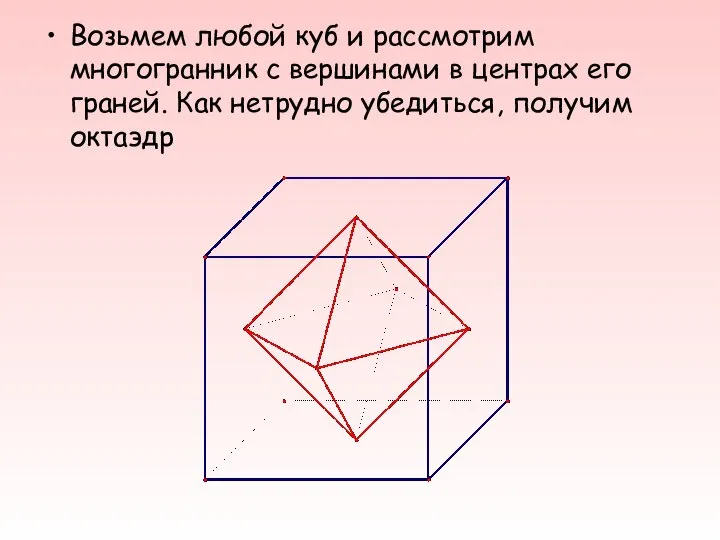
Двойственность правильных многогранников
Гексаэдр (куб) и октаэдр образуют двойственную пару многогранников. Число граней одного многогранника равно числу вершин другого и наоборот.

Возьмем любой куб и рассмотрим многогранник с вершинами в центрах его граней. Как нетрудно убедиться, получим октаэдр

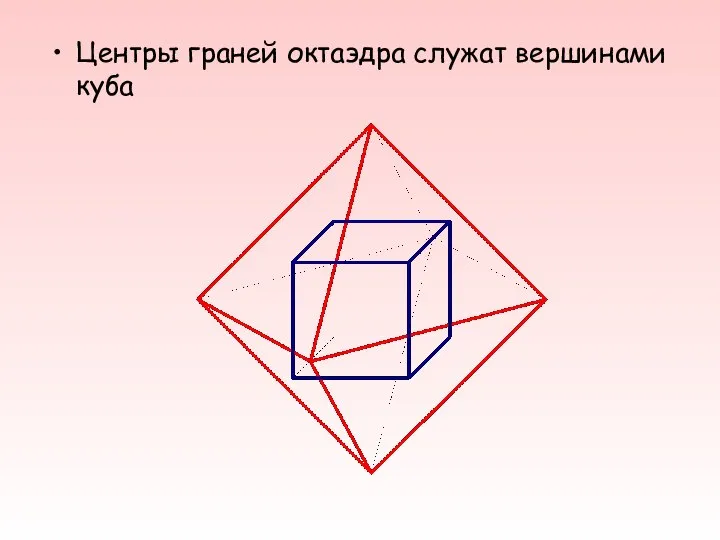
Центры граней октаэдра служат вершинами куба

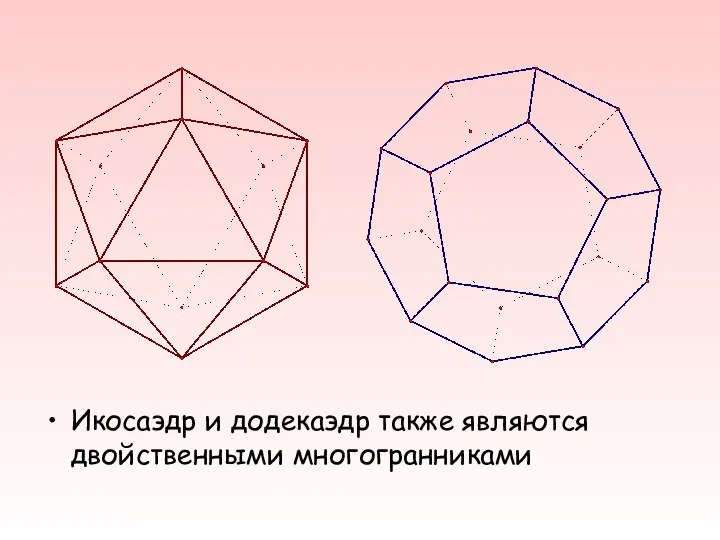
Икосаэдр и додекаэдр также являются двойственными многогранниками

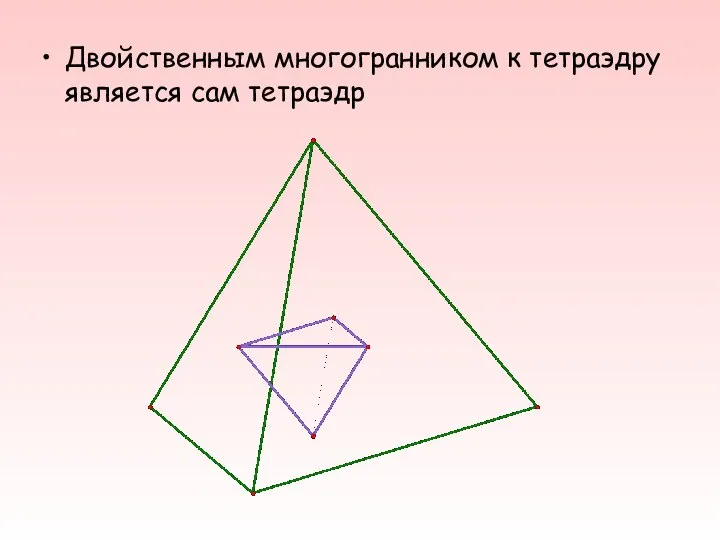
Двойственным многогранником к тетраэдру является сам тетраэдр