Содержание
- 2. Тригонометрическая форма записи комплексных чисел Тогда имеют место равенства: Следовательно, комплексное число z можно представить в
- 3. Действия над комплексными числами тогда произведение находится по формуле: Если комплексные числа заданы в тригонометрической форме:
- 4. Действия над комплексными числами Если комплексные числа заданы в тригонометрической форме:
- 5. Действия над комплексными числами Возведение в степень комплексного числа. Извлечение корня из комплексного числа.
- 6. Действия над комплексными числами Придавая k значения 0, 1, 2, …,n –1, получим n различных значений
- 7. Действия над комплексными числами Найти все значения кубического корня из единицы A В С
- 8. Показательная форма комплексного числа Рассмотрим показательную функцию от комплексной переменной z. Комплексные значения функции w определяются
- 9. Показательная форма комплексного числа Если в формуле (1) положим x = 0, то получим: Эта формула
- 10. Показательная форма комплексного числа Представим комплексное число z в тригонометрической форме:: По формуле Эйлера: Следовательно, всякое
- 12. Скачать презентацию









 Презентация на тему Векторы в пространстве
Презентация на тему Векторы в пространстве  Примеры на сложение
Примеры на сложение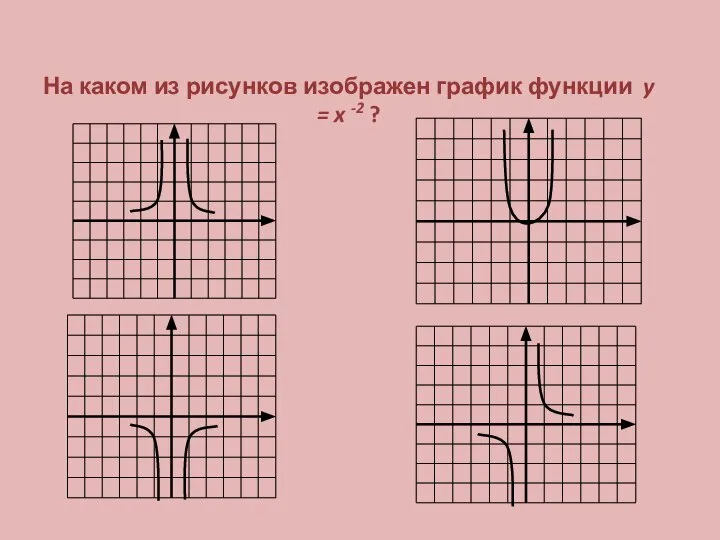 Степенная функция
Степенная функция Reshenie_zadach_1
Reshenie_zadach_1 Симметрия и асимметрия
Симметрия и асимметрия Задачи(БД)
Задачи(БД) Уравнение сферы
Уравнение сферы Исследование функции и построение графиков
Исследование функции и построение графиков Математический тренажёр. Устные упражнения на уроках математики в 7 классе как один из способов отработки навыка устного счёта
Математический тренажёр. Устные упражнения на уроках математики в 7 классе как один из способов отработки навыка устного счёта Разрез и сечение
Разрез и сечение Соотношения между сторонами и углами треугольника
Соотношения между сторонами и углами треугольника Правильные многоугольники
Правильные многоугольники Страна Математика
Страна Математика Теорема Пифагора
Теорема Пифагора Угол. Измерение углов
Угол. Измерение углов ИПАР по математике. Задача на проценты. Тема: математика в профессии моих родителей
ИПАР по математике. Задача на проценты. Тема: математика в профессии моих родителей urok TViMS NSV
urok TViMS NSV Матрицы. Виды матриц
Матрицы. Виды матриц Удивительный мир математики
Удивительный мир математики Приемы письменных вычислений
Приемы письменных вычислений Тригонометрия. Контрольная работа
Тригонометрия. Контрольная работа Решение задач на вычисление площади поверхности призмы
Решение задач на вычисление площади поверхности призмы Умножение и деление на 3
Умножение и деление на 3 Разные задачи. Урок 140
Разные задачи. Урок 140 Степенная функция
Степенная функция Расчёт надёжности систем с использованием экспоненциального закона распределения функции надёжности
Расчёт надёжности систем с использованием экспоненциального закона распределения функции надёжности Эквивалентные функции
Эквивалентные функции Булева алгебра
Булева алгебра