Содержание
- 2. Что может быть дискретно? Множества, с которыми мы работаем Шаги некоторого алгоритма Время
- 3. Что такое ДМ? Логика высказываний Логика предикатов Математическая логика Комбинаторика Теория алгоритмов Теория автоматов Теория графов
- 4. Теория автоматов и формальных языков Институт Информационных Технологий ЧелГУ, 2010
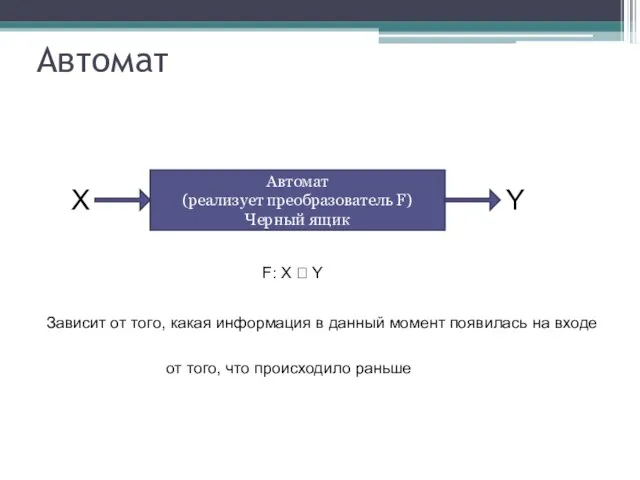
- 5. Автомат Автомат (реализует преобразователь F) Черный ящик X Y F: X ? Y Зависит от того,
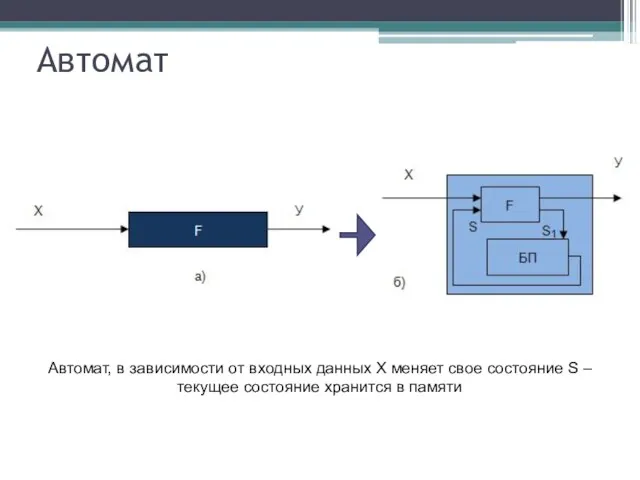
- 6. Автомат Автомат, в зависимости от входных данных Х меняет свое состояние S – текущее состояние хранится
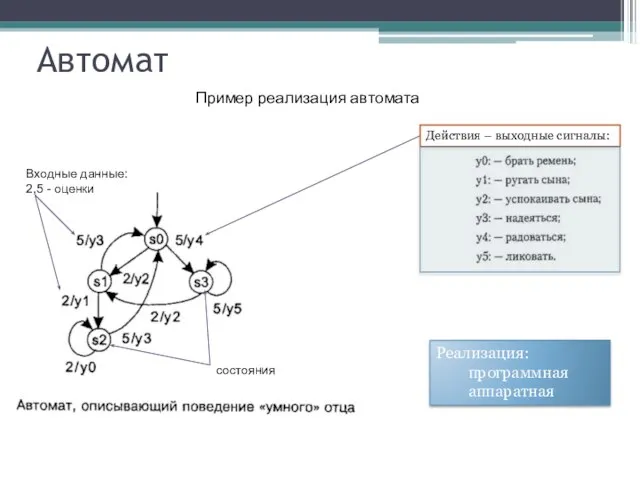
- 7. Автомат Пример реализация автомата Действия – выходные сигналы: Входные данные: 2,5 - оценки состояния Реализация: программная
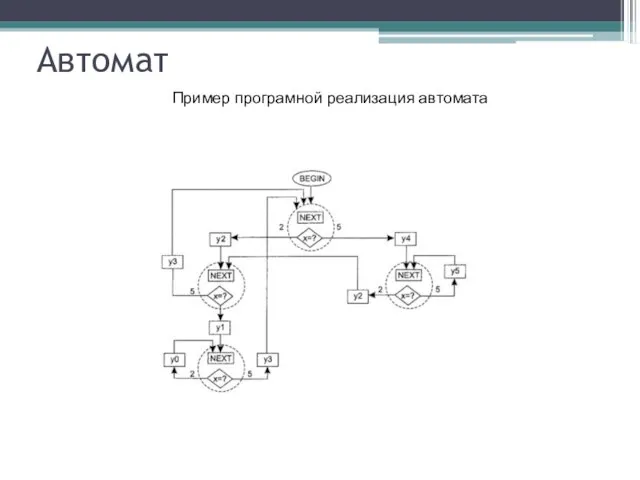
- 8. Автомат Пример програмной реализация автомата
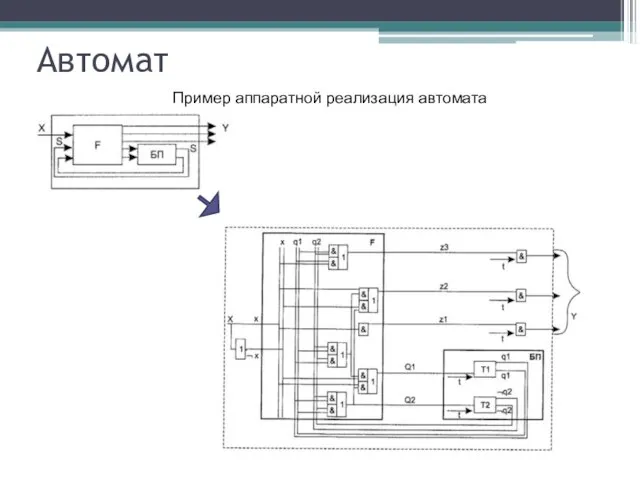
- 9. Автомат Пример аппаратной реализация автомата
- 10. Автомат Рассмотрим механизм управления лифтом. Если всего в здании N этажей, лифт может находится в одном
- 11. Автомат Это скучный слайд с терминологией - входной алфавит - выходной алфавит - набор внутренних состояний
- 12. Алфавитный оператор Это скучный слайд с терминологией Последовательности входных букв: называются входными словами. На вход автомату
- 13. Функции переходов и выходов Это скучный слайд с терминологией - функция переходов, если: - функция выходов,
- 14. Автоматы Мили и Мура Это скучный слайд с терминологией Автомат Мили: Автомат Мура: Автомат Мура всегда
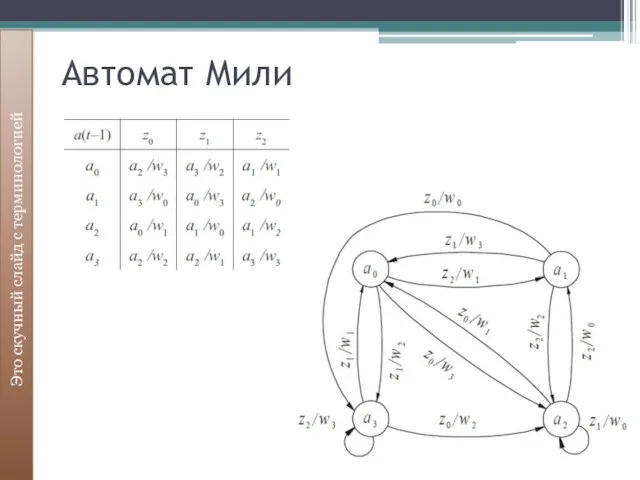
- 15. Автомат Мили Это скучный слайд с терминологией
- 16. Автомат Мили Это скучный слайд с терминологией
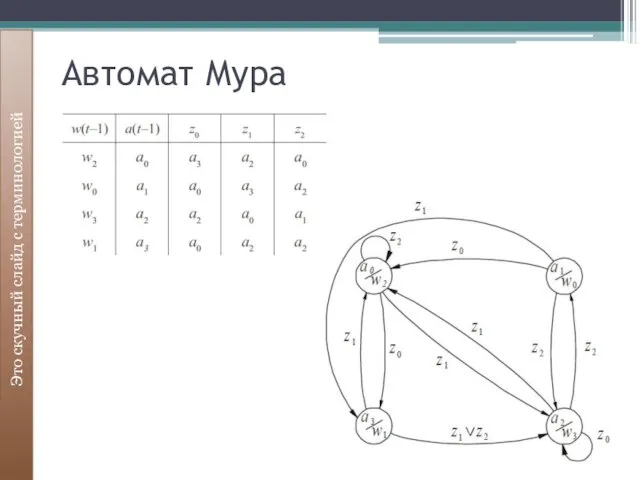
- 17. Автомат Мура Это скучный слайд с терминологией
- 18. Автомат Мура Это скучный слайд с терминологией
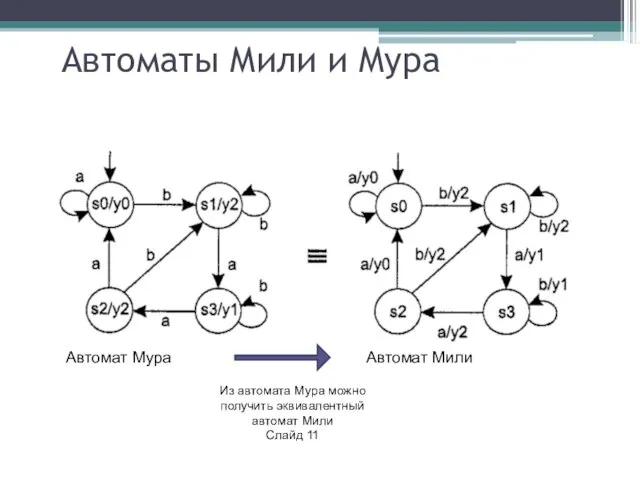
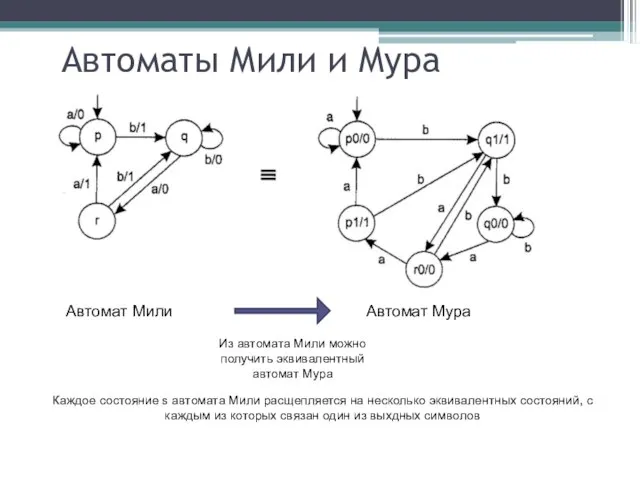
- 19. Автоматы Мили и Мура Автомат Мура Автомат Мили Из автомата Мура можно получить эквивалентный автомат Мили
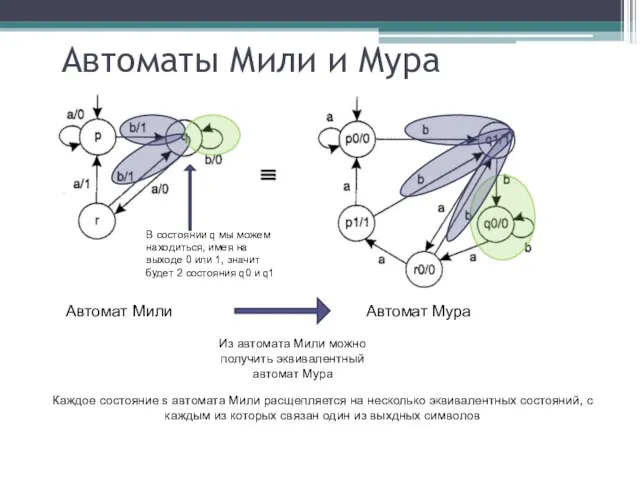
- 20. Автоматы Мили и Мура Автомат Мили Из автомата Мили можно получить эквивалентный автомат Мура Автомат Мура
- 21. Автомат Мили Из автомата Мили можно получить эквивалентный автомат Мура Автомат Мура Автоматы Мили и Мура
- 22. Условия «автоматности» оператора Это скучный слайд с терминологией - алфавитный оператор 1 осуществляет однозначное отображение из
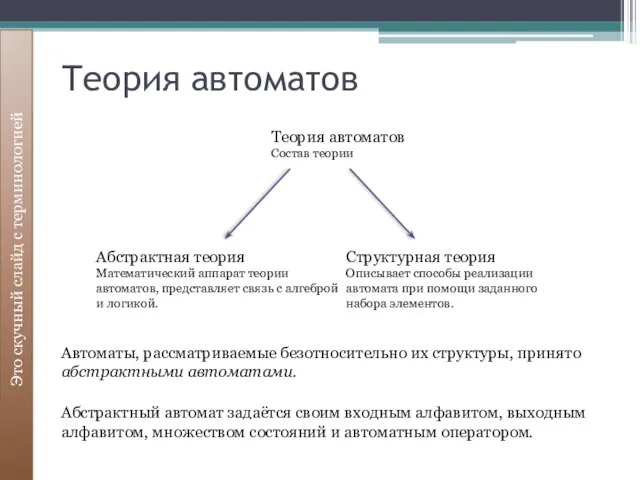
- 23. Теория автоматов Это скучный слайд с терминологией Теория автоматов Состав теории Абстрактная теория Математический аппарат теории
- 24. Теория автоматов и формальных языков Приложения теории автоматов Институт Информационных Технологий ЧелГУ, 2010
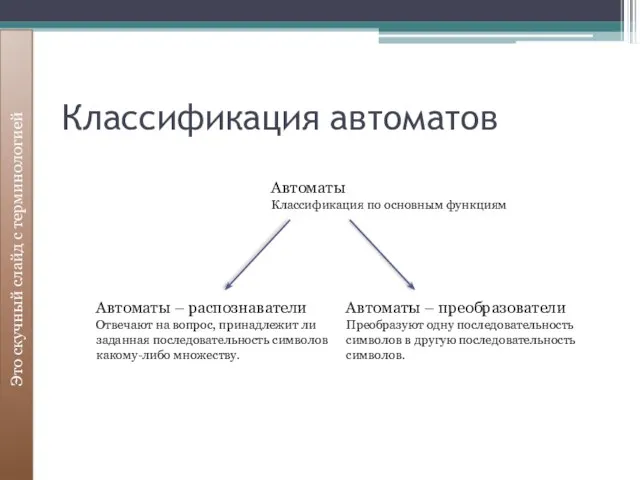
- 25. Классификация автоматов Это скучный слайд с терминологией Автоматы Классификация по основным функциям Автоматы – распознаватели Отвечают
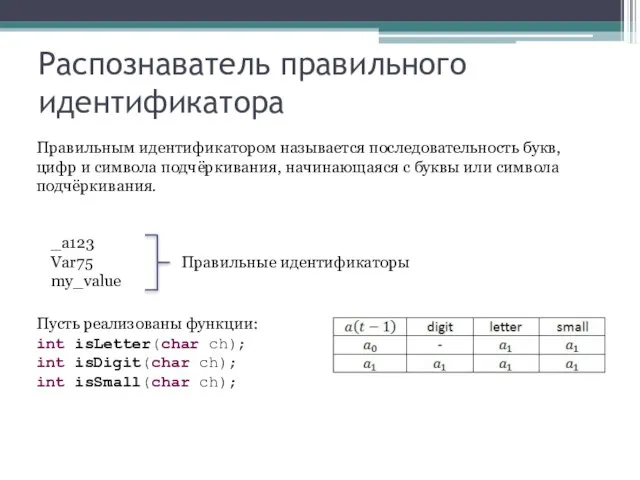
- 26. Распознаватель правильного идентификатора Правильным идентификатором называется последовательность букв, цифр и символа подчёркивания, начинающаяся с буквы или
- 27. Распознаватель правильного идентификатора Правильным идентификатором называется последовательность букв, цифр и символа подчёркивания, начинающаяся с буквы или
- 29. Скачать презентацию













 Презентация на тему Сечения многогранников
Презентация на тему Сечения многогранников  Заколдованные цифры
Заколдованные цифры Объёмные и плоские геометрические фигуры
Объёмные и плоские геометрические фигуры Случаи сложения вида +7
Случаи сложения вида +7 Матрица размера m x n
Матрица размера m x n Применение производной. Учебно-тренировочные материалы для подготовки к ЕГЭ
Применение производной. Учебно-тренировочные материалы для подготовки к ЕГЭ Собирательные числительные
Собирательные числительные Решение задач с помощью составления систем уравнений
Решение задач с помощью составления систем уравнений Параллелограмм
Параллелограмм Системы линейных уравнений
Системы линейных уравнений Устный счёт
Устный счёт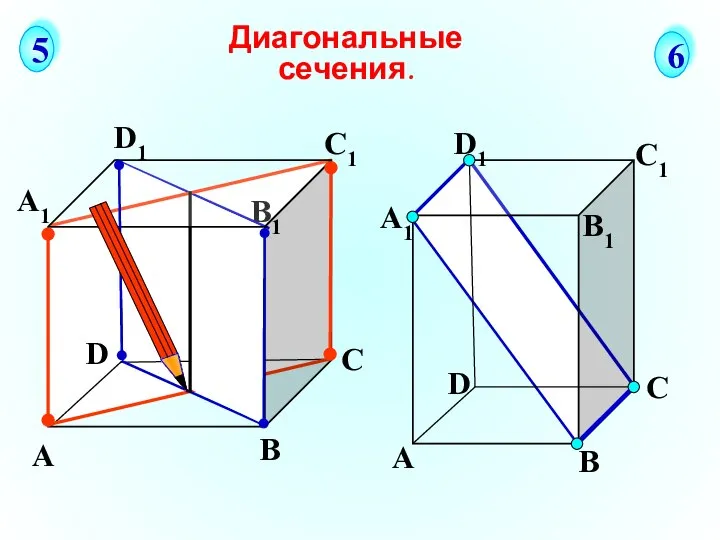 Диагональные сечения
Диагональные сечения Определение синуса, косинуса и тангенса угла
Определение синуса, косинуса и тангенса угла Метод координат
Метод координат Нахождение площади и периметра прямоугольника. Применение формул на практике
Нахождение площади и периметра прямоугольника. Применение формул на практике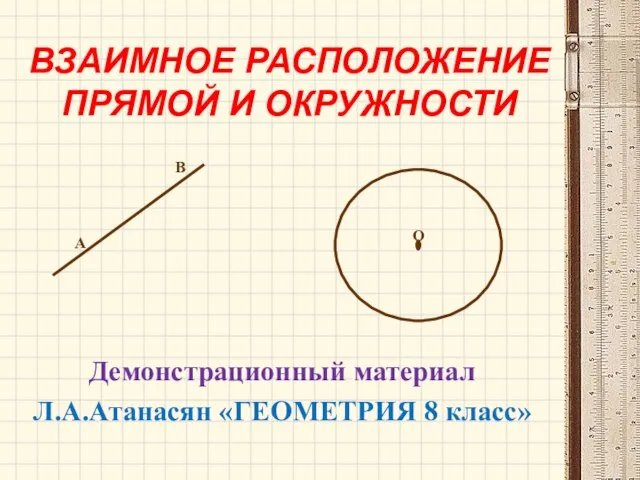 Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности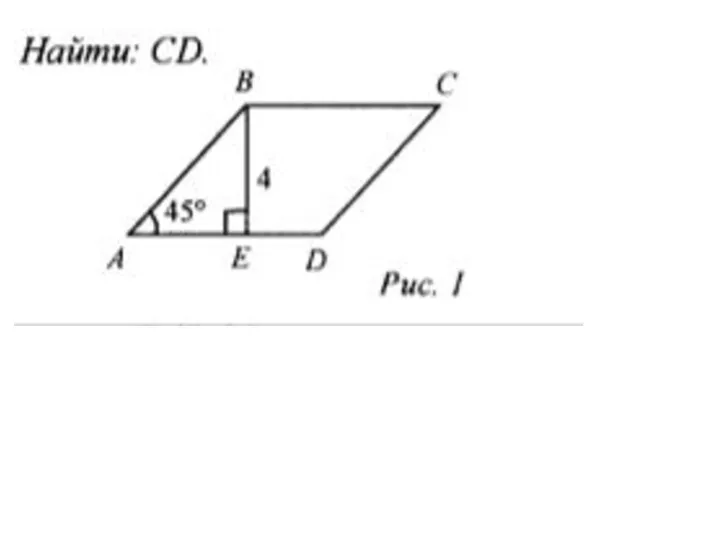 Вычисление площадей
Вычисление площадей Производная сложной функции
Производная сложной функции Обучающие слайды
Обучающие слайды Задача на процкеты
Задача на процкеты Презентация на тему Симметрия и движение (9 класс)
Презентация на тему Симметрия и движение (9 класс)  Составление систем уравнений Колмогорова. Математическое моделирование
Составление систем уравнений Колмогорова. Математическое моделирование Математический диктант по теме: Дроби. 6 класс
Математический диктант по теме: Дроби. 6 класс Дробная схватка
Дробная схватка Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Математика и здоровье. Математика и медицина
Математика и здоровье. Математика и медицина Тригонометрия. Контрольная работа
Тригонометрия. Контрольная работа Презентация на тему Центральные углы и углы, вписанные в окружность
Презентация на тему Центральные углы и углы, вписанные в окружность