Теорема Пифагора

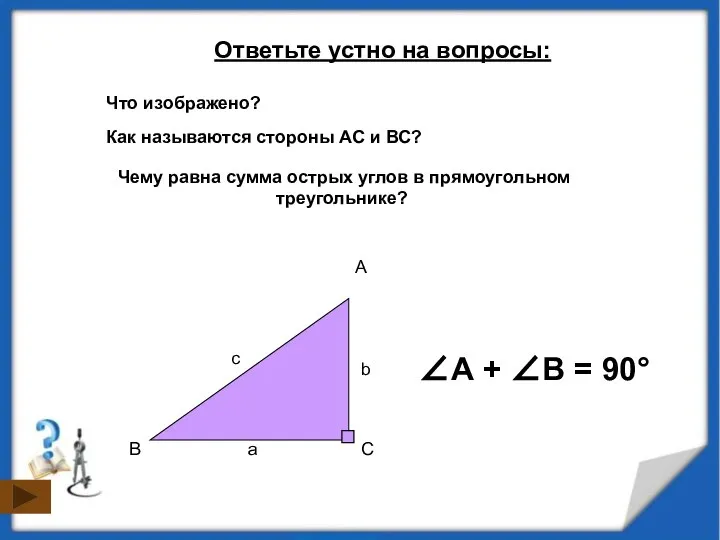
Что изображено?
Ответьте устно на вопросы:
Чему равна сумма острых углов в прямоугольном треугольнике?
∠А + ∠В = 90°
Как называются стороны АС и ВС?

Нужно знать зависимость между катетами и гипотенузой в прямоугольном треугольнике.
Эту зависимость подметили еще в глубокой древности и доказали теорему, которую знают теперь почти все школьники. Эта теорема носит имя Пифагора.

а
с
В прямоугольном треугольнике квадрат гипотенузы
равен сумме квадратов катетов
в
с2= а2 + в2
а – катет
в –катет
с –гипотенуза
письменно

Доказательство теоремы
Дано:
прямоугольный треугольник
а, в – катеты, с – гипотенуза
Доказать: с2= а2 + в2
Доказательство:
Достроим треугольник до квадрата со стороной а+в;
S=(а+в)2 - площадь квадрата
Четыре прямоугольных треугольника, S = ½ ав
S= 4*1/2ав+с2 =2ав+с2
(а+в)2 = 2ав+с2
с2= а2 + в2
а
а
а
а
с
с
с
с
в
в
в
в
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
письменно

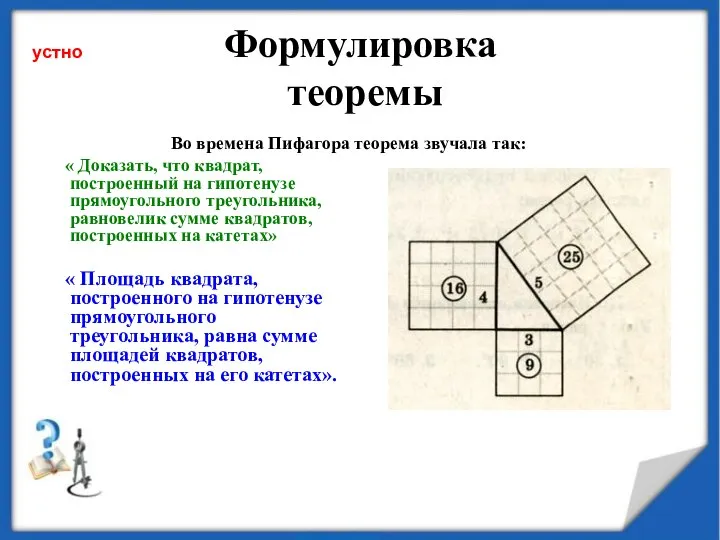
Формулировка
теоремы
« Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах»
« Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах».
Во времена Пифагора теорема звучала так:
устно

Немного истории
Для нас Пифагор – математик. В древности было иначе. Геродот называет его "выдающимся софистом", то есть учителем мудрости. Для своих современников Пифагор прежде всего был религиозным пророком, воплощением высшей божественной мудрости. Пифагор был разносторонней личностью. Он занимался и медициной, и музыкой, и астрономией, а так же был четыре раза подряд олимпийским чемпионом.
устно

Пифагор Самосский - это древнегреческий математик, философ и мистик, родоначальник школы пифагорейцев. Годы его жизни - 570-490 гг. до н. э.
Немного истории
устно

Значение теоремы Пифагора
Теорема Пифагора- это одна из самых важных теорем геометрии. Значение её состоит в том, что из неё или с её помощью можно вывести большинство теорем геометрии.
устно

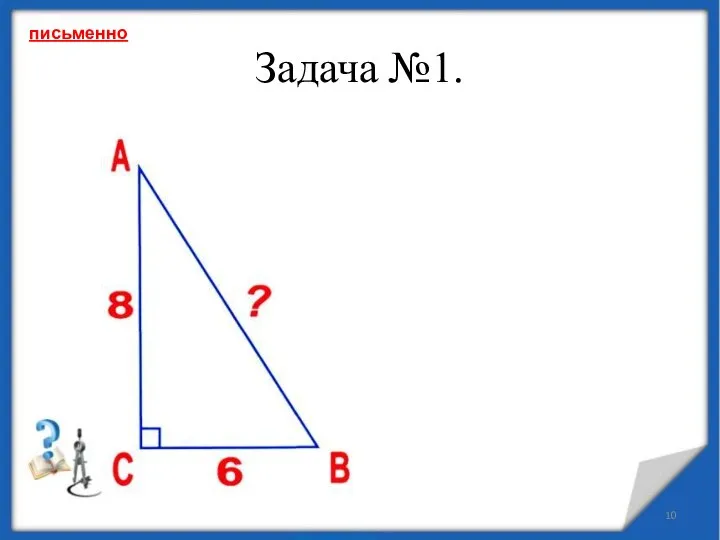
Задача №1.
письменно

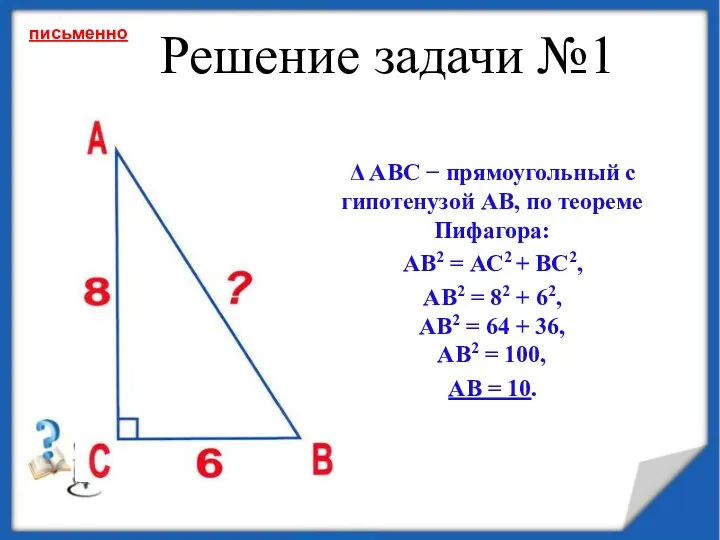
Решение задачи №1
Δ АВС − прямоугольный с гипотенузой АВ, по теореме Пифагора:
АВ2 = АС2 + ВС2,
АВ2 = 82 + 62, АВ2 = 64 + 36, АВ2 = 100,
АВ = 10.
письменно

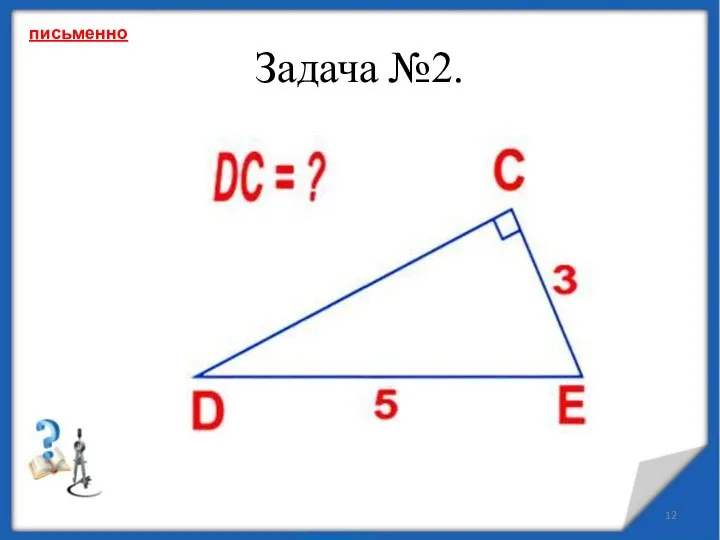
Задача №2.
письменно

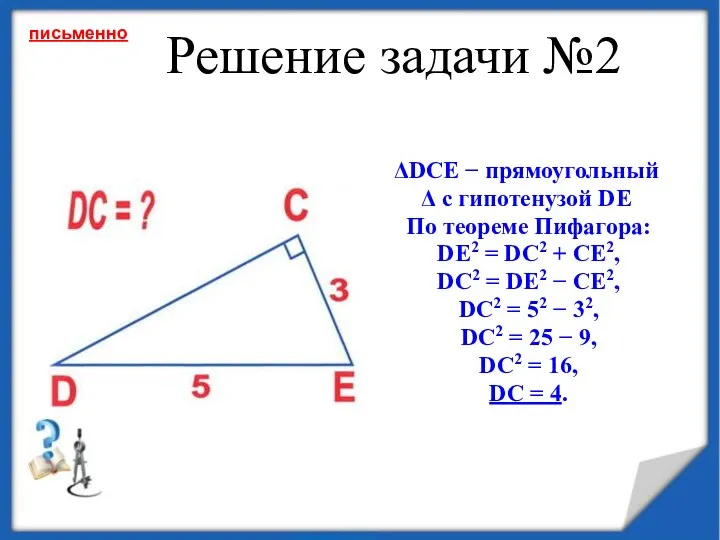
Решение задачи №2
DCE − прямоугольный
с гипотенузой DE
По теореме Пифагора:
DE2 = DС2 + CE2,
DC2 = DE2 − CE2,
DC2 = 52 − 32,
DC2 = 25 − 9,
DC2 = 16,
DC = 4.
письменно

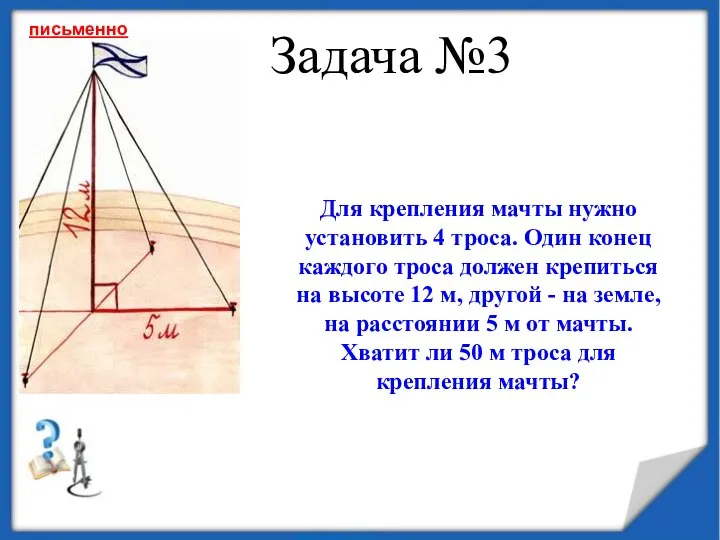
Задача №3
Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой - на земле, на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты?
письменно