Содержание
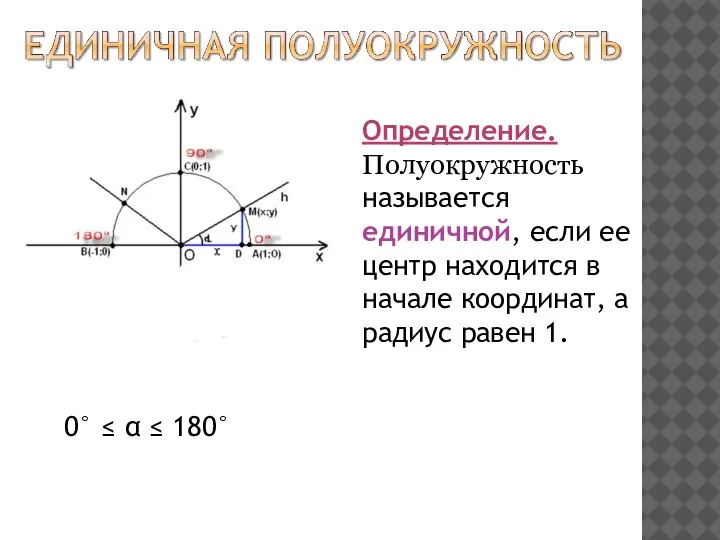
- 2. 0° ≤ α ≤ 180° Определение. Полуокружность называется единичной, если ее центр находится в начале координат,
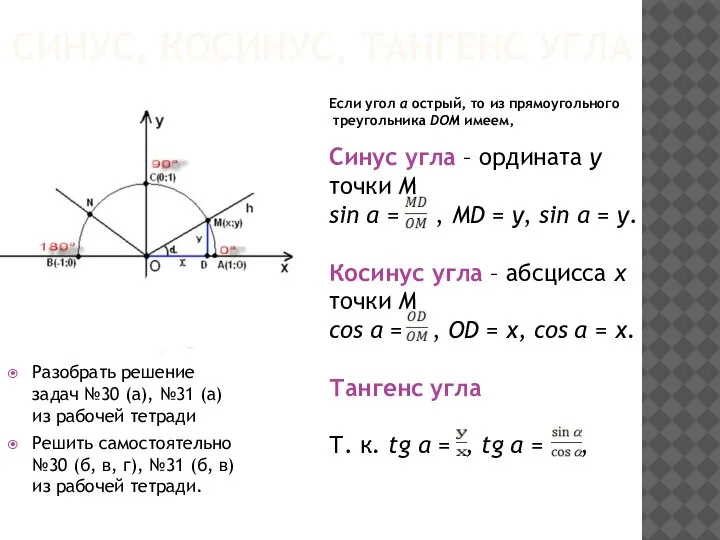
- 3. Если угол α острый, то из прямоугольного треугольника DOM имеем, Синус угла – ордината у точки
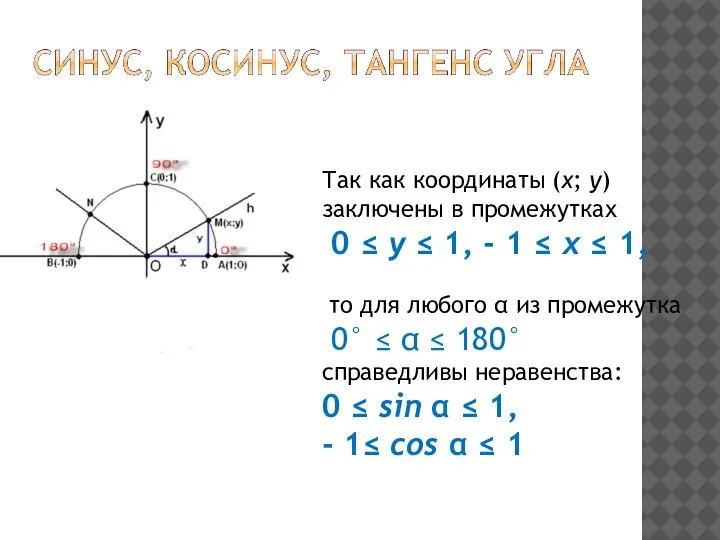
- 4. Так как координаты (х; у) заключены в промежутках 0 ≤ у ≤ 1, - 1 ≤
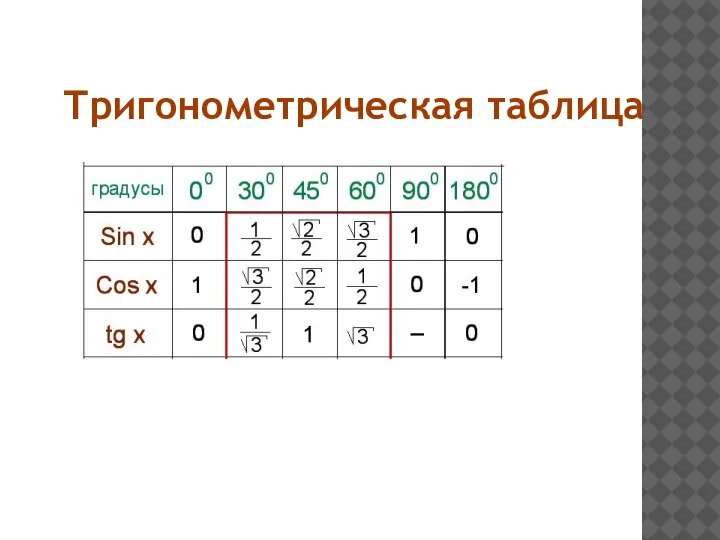
- 5. Тригонометрическая таблица
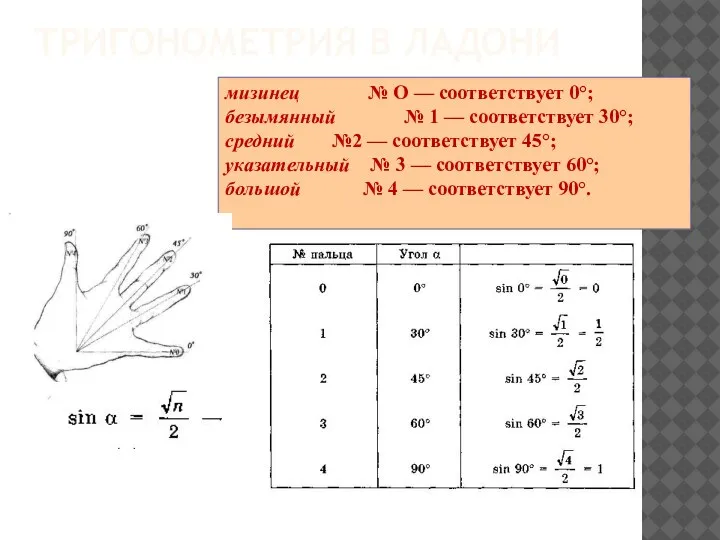
- 6. ТРИГОНОМЕТРИЯ В ЛАДОНИ мизинец № О — соответствует 0°; безымянный № 1 — соответствует 30°; средний
- 8. Скачать презентацию
 Урок математики в 1 классе Тема: «Сложение и вычитание в пределах 10. Закрепление» Образовательная система: «Школа России» Состави
Урок математики в 1 классе Тема: «Сложение и вычитание в пределах 10. Закрепление» Образовательная система: «Школа России» Состави Исследование функции с помощью производной
Исследование функции с помощью производной 20171212_prezentatsiya_k_urokuарифметические действия над обыкновенными дробями и смешанными числами
20171212_prezentatsiya_k_urokuарифметические действия над обыкновенными дробями и смешанными числами Презентация на тему УСТНЫЙ СЧЕТ
Презентация на тему УСТНЫЙ СЧЕТ  Задания по математике (5 класс, часть 2)
Задания по математике (5 класс, часть 2) Площадь эллипса и окружности
Площадь эллипса и окружности Презентация на тему Параллельные прямые в пространстве
Презентация на тему Параллельные прямые в пространстве  Задачи на разрезания и перекраивания фигур
Задачи на разрезания и перекраивания фигур Золотое сечение
Золотое сечение Математическая статистика. Лекция 2
Математическая статистика. Лекция 2 Вычислить интеграл
Вычислить интеграл Проверь свои знания. Игра для девятиклассников
Проверь свои знания. Игра для девятиклассников Презентация на тему Нумерация в пределах 1000
Презентация на тему Нумерация в пределах 1000  Квадратный корень
Квадратный корень Задача №1. Лабораторная работа №5
Задача №1. Лабораторная работа №5 Обыкновенные дроби. Тест с заполнением пропусков
Обыкновенные дроби. Тест с заполнением пропусков Математика в лицах.11б
Математика в лицах.11б ОДУ высших порядков
ОДУ высших порядков Уравнение (урок математики, 5 класс)
Уравнение (урок математики, 5 класс) Математический калейдоскоп. Мероприятие для учащихся 5 классов
Математический калейдоскоп. Мероприятие для учащихся 5 классов Доказательство неравенств
Доказательство неравенств Действия над комплексными числами
Действия над комплексными числами Проектирование точки на плоскости
Проектирование точки на плоскости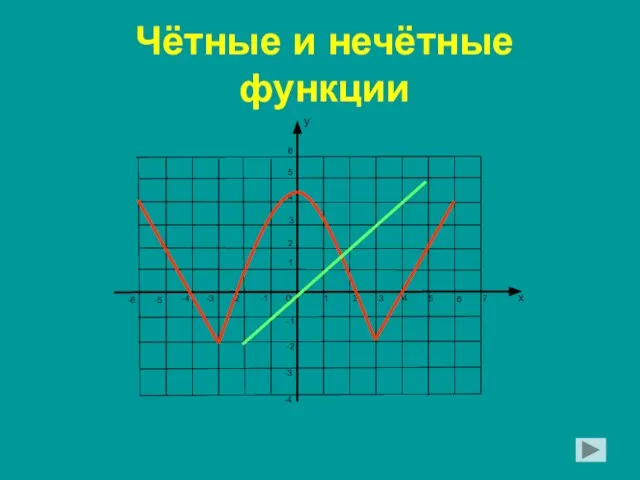 Презентация на тему Чётные и нечётные функции
Презентация на тему Чётные и нечётные функции  Sıralama algoritmaları
Sıralama algoritmaları Презентация на тему Прибавление числа 5 (1 класс)
Презентация на тему Прибавление числа 5 (1 класс)  Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю Презентация по математике "Единицы длины. Метр" -
Презентация по математике "Единицы длины. Метр" -