Алгебра высказываний

Изучить литературу.
Прослушать лекцию.
Разработать конспект.

Если дана некоторая формула F и каждой ее пропозициональной переменной приписано значение "и" или "л", то говорят что дана интерпретация формулы F.
Все множество формул логики высказываний можно разбить на три класса: тождественно истинные, тождественно ложные и теоремы. В каждом классе может быть перечислимое и счетное множество формул.
Поиск алгоритма, определяющего к какому классу принадлежит та или иная формула, формирует проблему разрешимости исчисления высказываний.

Отношение
равносильности формул

Определение. Две формулы F1 и F2 называют равносильными (F1 ≡ F2), если они имеют одинаковое значение «истина» или «ложь» при одинаковых наборах пропозициональных переменных. Если две формулы равносильны F1 ≡ F2, то они эквивалентны между собой, т.е. (F1↔F2). И наоборот, если формулы эквивалентны (F1↔F2), то они равносильны (F1 ≡ F2).

Истинностные функции

Совершенные нормальные формы истинностных функций функций

Дизъюнктивная и конъюнктивная нормальные формы формулы (ДНФ и КНФ).
Формулы, построенные особым образом из высказывательных переменных с помощью только операций дизъюнкции, конъюнкции и отрицания, называют ДИЗЪЮНКТИВНЫМИ и КОНЪЮНКТИВНЫМИ НОРМАЛЬНЫМИ ФОРМАМИ (ДНФ и КНФ).
Пусть задана система высказывательных переменных (x1,x2,…,xn). Элементарной дизъюнкцией высказывательных переменных из системы называется дизъюнкция некоторых высказывательных переменных этой системы или их отрицаний.

Дизъюнктивная и конъюнктивная нормальные формы формулы (ДНФ и КНФ).
ЭЛЕМЕНТАРНОЙ КОНЪЮНКЦИЕЙ называется конъюнкция некоторых высказывательных переменных этой системы или их отрицаний. Если в элементарную дизъюнкцию (конъюнкцию) входит каждое высказывательное переменное из системы (с отрицанием или без него) и притом только один раз, то она называется ПОЛНОЙ ЭЛЕМЕНТАРНОЙ ДИЗЪЮНКЦИЕЙ (КОНЪЮНКЦИЕЙ).

Формула F называется КОНЪЮНКТИВНОЙ НОРМАЛЬНОЙ ФОРМОЙ (КНФ) от высказывательных переменных системы, если она является конъюнкцией элементарных дизъюнкций, образованных из высказывательных переменных этой системы.
Формула F называется ДИЗЪЮНКТИВНОЙ НОРМАЛЬНОЙ ФОРМОЙ (ДНФ) от высказывательных переменных системы, если она является дизъюнкцией элементарных конъюнкций, образованных из этих переменных.

Совершенные нормальные формы удобно записывать, используя таблицы истинности, по значениям пропозициональных переменных и значению описываемой формулы.
Элементарные коньюнкции СДНФ формируются для значений формулы “И”. Число элементарных коньюнкций равно числу истинных значений формулы.
Пропозициональные переменные, входящие в элементарную коньюнкцию, записываются без изменений, если их значение равно “И” и с логической связкой “⎤”, если их значение равно “Л”.

Совершенные нормальные формы удобно записывать, используя таблицы истинности, по значениям пропозициональных переменных и значению описываемой формулы.
Элементарные дизьюнкции СКНФ формируются для значений формулы “Л”. Число элементарных дизьюнкций равно числу ложных значений формулы. Пропозициональные переменные, входящие в элементарную дизьюнкцию, записываются без изменений, если их значение равно “Л” и с логической связкой “⎤”, если их значение равно “И”.

Пример. Записать СДНФ и СКНФ для функции, заданной таблицей истинности.

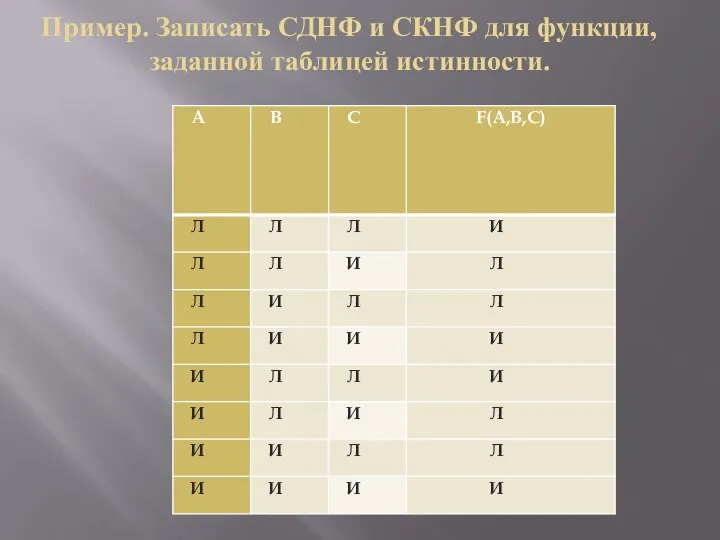
Пример. Записать СДНФ и СКНФ для функции, заданной таблицей истинности.
a) Формула СДНФ:
F(A,B,C) =
=(⎤А∧⎤B∧⎤C)∨(⎤А∧B∧⎤C)∨(А∧⎤B∧⎤C)∨(А∧B∧C);
b) Формула СКНФ:
F(A,B,C) =
=(A∨B∨⎤C) ∧(A∨⎤B∨C) ∧(⎤A∨B∨⎤C)∧(⎤A∨⎤B∨C).

Полные системы истинностных функций

Система истинностных функций называется полной, если с помощью функций этой системы можно выразить любую истинностную функцию.
{⎤, ∧, ∨}
{⎤, ∧}
{⎤, ∨}
{⎤, →}
{|}
{↓}

.
Формулы
Общезначимая (тавтология, тождественно истинная ╞ )
Невыполнимая (противоречие, тождественно невыполнимая)
Нейтральная
Выполнимая
Необщезначимая

.
Важнейшие общезначимые формулы.

Формула, построенная на пропозициональных букв А1, А2, …, An и их отрицаний ¬А1, ¬А2, …, ¬An с помощью только символов логических операций ˄ и ∨.
А+ - формула, полученная заменой ˄ на ∨, ∨ на ˄ каждой пропозициональной буквы Аi на ¬Аi и наоборот.
Тогда ¬А≡А+ .

Предложение 1.
Формула ╞E, построенная на атомах Р1, Р2, …, Рn ,
тогда формула ╞Е*, полученная из Е одновременной подстановкой формул А1, А2, …, An вместо Р1, Р2, …, Рn соответственно.

(Подстановка вместо атомов.)
Предложение 1
Пусть Е - формула, в которую входят только атомы Р1,...., Рn а Е* - формула, полученная из Е одновременной подстановкой формул А1, ...,Аn вместо P1, ..., Рn соответственно.
Если ╞ Е, то ╞ Е*.

Предложение 2.
Если ╞А и ╞А→В,
то ╞В.

Предложение 3.
╞А↔В тогда и только тогда,
когда А≡В.

Предложение 4.
╞Е тогда и только тогда,
когда ¬Е – противоречие.

(Подстановка вместо атомов.)
Предложение 2
Если ╞ А и ╞ А→В, то ╞ В.
Предложение 3
╞ А ↔В тогда и только тогда, когда А≡ В.
Предложение 4.
╞ E и тогда и только тогда, когда
¬E – противоречие.

Пример. Пусть А есть ¬А˄(¬В∨С), тогда ¬А≡А∨ (В˄¬С).
Упражнение. Постройте формулы отрицания :
(1) (А ∨¬В) ˄ А ˄ (¬С∨А)˄С;
(2) ¬А˄(В∨¬С) ∨А˄¬В;
(3) В∨С ∨¬А∨ (А∨¬С).

Предложение. (принцип двойственности).
Пусть А и В – формулы такого же вида, что и в предложении 3. А* и В* – формулы, построенные на А и В заменой ˄ на ∨, ∨ на ˄. Тогда:
(а) Если ╞¬А , то ╞ А* ;
(b) Если ╞ А , то ╞ ¬А* ;
(c) Если ╞ А↔В, то ╞ А*↔В*;
(d) Если ╞A⟼B , то ╞ B*⟼A* .
Доказательство.

Пример.
А =(А ˄¬А)
╞¬А ╞¬(А ˄¬А) ;
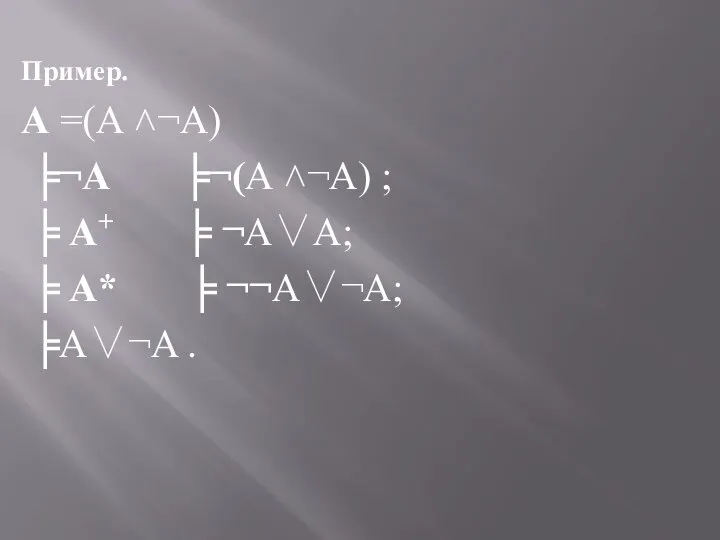
╞ А+ ╞ ¬А∨А; ╞ А* ╞ ¬¬A∨¬A;
╞A∨¬A .

Правила замены и подстановки расширяют возможности эквива­лентных преобразований формул сложных высказываний.

Важнейшие общезначимые формулы
Теорема. Следующие формулы алгебры высказываний являются тавтологиями:
Закон исключенного третьего
Закон отрицания противоречия
Закон двойного отрицание
Закон тождества
Закон контрапозиции
Закон силлогизма (правило цепного заключения)
Закон противоположности
Правило добавления антецедента («истина из чего угодно»)
Правило «из ложного – что угодно»
Правило модус поненс (m. p.)
Правило модус толленс (m.t.)
Правило перестановки посылок
Правило объединения (и разъединения) посылок
Правило разбора случаев
Правило привидения к абсурду ;

.
Лекция 4
1..Исчисление высказываний.
2. Понятие булевой функции.
3. Элементарные функции. ДНФ и КНФ.
4. Контактные схемы.

Умозаключение - это мысль, в ходе которой из одного или нескольких суждений выводится новое суждение.
При этом исходные суждения называются ПОСЫЛКАМИ, а полученное суждение - ЗАКЛЮЧЕНИЕМ или СЛЕДСТВИЕМ. Аристотель приводил такой пример умозаключения: "Все люди смертны" и "Сократ - человек" - посылки. "Сократ смертен" - заключение. Переход от посылок к заключению происходит по ПРАВИЛАМ ВЫВОДА и законам логики.
ПРАВИЛО 1: Если посылки умозаключения истинны, то истинно и заключение.
ПРАВИЛО 2: Если умозаключение справедливо во всех случаях, то оно справедливо и в каждом частном случае. (Это правило ДЕДУКЦИИ - переход от общего к частному.)
ПРАВИЛО 3: Если умозаключение справедливо в некоторых частных случаях, то оно справедливо во всех случаях. (Это правило ИНДУКЦИИ - переход от частного к общего).

Важнейшие правила следования.
16. Если Г |=¬( А ∨В), то Г |= ¬А˄¬В.
(Удаление отрицания дизъюнкции УОД).
17. Если Г |=¬(А→В), то Г |= А˄¬В.
(Удаление отрицания импликации УОИ).
18. Если Г |= ¬(А↔В), то Г |=(А∨В)˄¬(А˄В).
(Удаление отрицания эквиваленции УОЭ).
19. Если Г |=А→В и Г |=В→С, то Г |= А→С.
(Силлогизм С).
.

Важнейшие правила следования.
20. Если Г |= А →В, то Г |= ¬В→¬А.
(Контрапозиция К).
21. Если Г |=¬В и Г |=А→В, то Г |= ¬А.
(Modus tollens MT).
22. Если Г |= (А∨В) и Г |= ¬А, то Г|=В.
(Дизъюнктивный силлогизм ДС).
23. Если Г |=А→(В→С), то Г |= А˄В→С.
(Соединение посылок СП).
.

Важнейшие правила следования.
24. Если Г |= А˄В→С, то Г |= А→(В→С).
(Разъединение посылок РП).
25. Если Г |=А→(В→С), то Г |= В→(А→С).
(Перемена посылок ПП).
26. Если Г |= А→В, Г |=С→D, Г |=А∨С,
то Г |=В∨D . (Конструктивная дилемма КД).
27. Если Г |= А→В, Г |=С→D, Г |=¬В∨¬D,
то Г |=¬А∨¬С. (Деструктивная дилемма ДД).
.

1. Дано F=(F1→F2) →((F2→F3) →(F1∨F2 →F3).
Выполнить преобразования для упрощения алгебраического выражения.
Удалить всюду логическую связку “→”:
F= ⎤(⎤F1∨F2)∨(⎤( ⎤F2∨F3)∨(⎤(F1∨F2) ∨F3);
Опустить отрицание на элементарные формулы по закону де Моргана:
F=F1∧⎤F2∨F2∧⎤F3∨⎤F1∧⎤F2∨F3;
Выполнить преобразование по закону дистрибутивности:
F=( F1∨⎤F1) ∧⎤F2∨F2∧⎤F3∨ F3;
Удалить член ( F1∨⎤F1), так как ( F1∨⎤F1)=и:
F=⎤F2∨F2∧⎤F3∨ F3;
Выполнить преобразование по закону дистрибутивности:
F=⎤F2∨(F2∨F3) ∧(⎤F3∨ F3);
Удалить член ( F3∨⎤F3)=и:
F=⎤F2∨(F2∨F3); Применить закон ассоциативности:
F=(⎤F2∨F2)∨F3; Приравнять “истине” значение формулы F, т.к.⎤F2∨F2)=и: F=и∨F3=и.

2. Дано F=⎤(F1→F2)∧(⎤F3∨⎤F4)∨⎤(F1∨F2)∧⎤(F3∧F4).
Выполнить эквивалентные преобразования для упрощения алгебраического выражения.
Удалить логическую связку “→”:
F=⎤(⎤F1∨F2)∧(⎤F3∨⎤F4)∨⎤(F1∨F2)∧⎤(F3∧F4);
Опустить отрицание на элементарные формулы по закону де Моргана:
F=F1∧⎤F2∧(⎤F3∨⎤F4)∨ ⎤ F1∧⎤F2∧(⎤F3∨⎤F4);
Выполнить преобразование по закону дистрибутивности:
F=( F1∨⎤ F1) ∧⎤F2∧(⎤F3∨⎤F4);
Удалить член ( F1∨⎤F1)=и:
F=⎤F2∧(⎤F3∨⎤F4).
Дальнейшее упрощение формулы F невозможно.

Алгоритм приведения к нормальной форме
Шаг 1. Устранить логические связки
“↔” и “→” всюду по правилам:
F1 ↔ F2 =(F1→F2)∧(F2→F1)=(⎤ F1∨ F2)∧(⎤ F2∨ F1)=(⎤ F1∧⎤ F2)∨( F1∧ F2);
F1 → F2 =⎤ F1∨F2 =⎤ (F1 ∧(⎤ F2)).

Алгоритм приведения к нормальной форме
Шаг 2
Продвинуть отрицание до элементарной формулы (пропозициональной переменной) по правилам:
⎤(⎤ F) = F ;
⎤(F1∨ F2 ) = (⎤ F1) ∧(⎤ F2);
⎤(F1∧F2) = (⎤ F1)∨(⎤ F2).
.

Алгоритм приведения к нормальной форме
Шаг 3
Применить закон дистрибутивности:
для КНФ:
F1∨(F2 ˄F3) = (F1∨ F2)˄(F1∨F3);
b) для ДНФ:
F1∧(F2∨ F3) = (F1∧F2)∨(F1∧F3).

Пример: Дана формула F=((F1→(F2∨⎤F3))→F4).
Привести формулу к виду КНФ:
1) F=(⎤F1∨(F2∨⎤ F3))→F4 ;
2) F=⎤(⎤F1∨(F2∨⎤F3))∨F4 ;
3) F=(F1∧(⎤ F2)∧ F3)∨F4 ;
4) F=(F4∨F1)∧(F4∨(⎤F2)∧F3);
5) F=(F4∨F1)∧(F4∨⎤F2)∧(F4∨F3).

Пример:
Дана формула F=(⎤(F1∧F2)(F1∨F2)).
Привести формулу к виду ДНФ:
F=(⎤F1∨⎤F2)˄(F1∨F2);
F=((⎤F1∨⎤F2)∧F1)∨ ((⎤F1∨⎤F2) ∧ F2);
F=(⎤F1 ∧ F1)∨(⎤F2 ∧ F1)∨ (⎤F1 ∧ F2) ∨(⎤F2 ∧ F2);
F=(⎤F2 ∧ F1)∨ (⎤F1 ∧ F2).

Если каждая элементарная конъюнкция (или элементарная дизъюнкция) формулы содержат символы всех пропозициональных переменных, то такая формула называется совершенной.
Есть совершенные дизъюнктивные нормальные формы формулы (СДНФ) и совершенные конъюнктивные нормальные формы формулы (СКНФ).

Алгоритм преобразования ДНФ к виду СДНФ.
Шаг 1:
если в элементарную конъюнкцию F не входит подформула Fi или ⎤Fi, то дополнить элементарную конъюнкцию высказыванием (Fi∨⎤Fi) и выполнить преобразование формулы по закону дистрибутивности:
F∧(Fi∨⎤Fi)= F∧ Fi∨ F∧⎤Fi;
Шаг 2:
если в элементарную конъюнкцию F не входит подформула Fj или ⎤Fj, то повторить шаг 1, иначе – конец.

Преобразовать формулу к виду СДНФ:
F=F1∧⎤F2∧(F3∨⎤F3) ∨ F1∧⎤F3∧F4˄(F2∨⎤F2) ∨F1˄F2˄F3˄⎤F4;
1) F=F1∧⎤F2∧F3∨F1∧⎤F2∧⎤F3∨F1∧F2∧⎤F3∧F4∨F1∧⎤F2∧⎤F3∧F4∨ F1∧F2∧F3∧⎤F4;
2) F=F1∧⎤F2∧F3∧(F4∨⎤F4)∨F1∧⎤F2∧⎤F3∧(F4∨⎤F4)∨F1∧F2∧⎤F3∧F4∨ F1∧⎤F2∧⎤F3∧F4∨ F1∧F2∧F3∧⎤F4;
3) F=(F1∧⎤F2∧F3∧F4)∨(F1∧⎤F2∧F3∧⎤F4)∨(F1∧⎤F2∧⎤F3∧F4);
4)
(F1∧⎤F2∧⎤F3∧⎤F4)∨ (F1∧F2∧⎤F3∧F4)∨ (F1∧⎤F2∧⎤F3∧F4)∨ (F1∧F2∧F3∧⎤F4).

Пример. Дано F=(F1∨F2)∧(⎤F1∨⎤F2∨F3∨F4).
Преобразовать формулу к виду СКНФ.
1) F=(F1∨F2∨F3∧⎤F3) ∧(⎤F1∨⎤F2∨F3∨F4);
2) F=(F1∨F2∨F3) ∧(F1∨F2∨⎤F3) ∧(⎤F1∨⎤F2∨F3∨F4);
3) F=(F1∨F2∨F3∨F4∧⎤F4)∧(F1∨F2∨⎤F3∨F4∧⎤F4)∧ ∧(⎤F1∨⎤F2∨F3∨F4);
4) F=(F1∨F2∨F3∨F4)∧(F1∨F2∨F3∨⎤F4)∧(F1∨F2∨⎤F3∨F4) ∧(F1∨F2∨⎤F3∨⎤F4) ∧(⎤F1∨⎤F2∨F3∨F4).

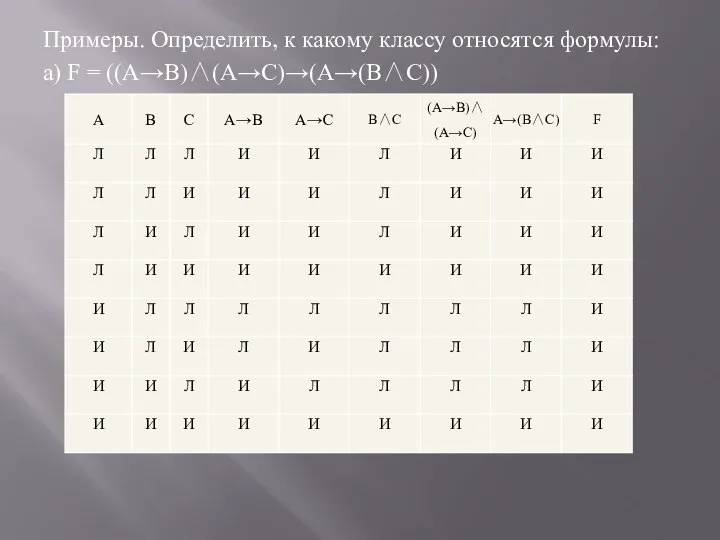
Примеры. Определить, к какому классу относятся формулы:
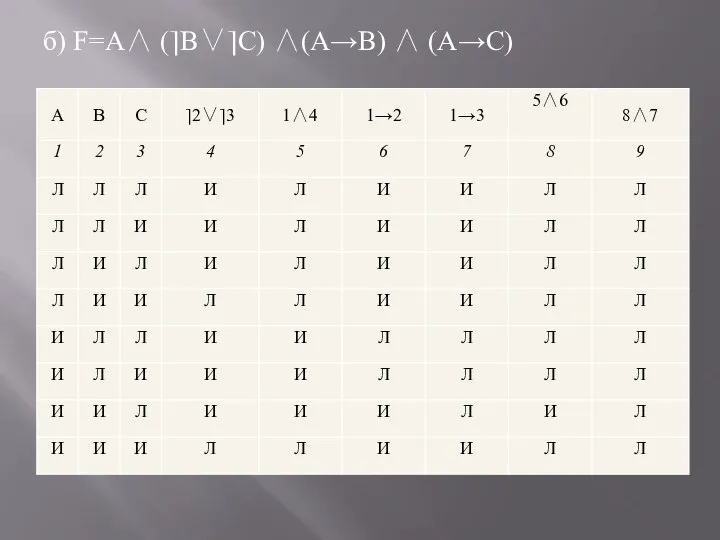
a) F = ((A→B)∧(A→C)→(A→(B∧C))

б) F=A∧ (⎤B∨⎤C) ∧(A→B) ∧ (A→C)

Любая формула исчисления высказываний может рассматриваться как формула алгебры высказываний и, следовательно, можно рассматривать ее логические значения на различных наборах значений входящих в нее пропозициональных переменных по таблицам истинности.
Недостаток использования таблиц истинности состоит в том, что при большом числе пропозициональных переменных сама процедура построения этих таблиц становится громоздкой, так как число строк этой таблицы равно 2n , где n - число пропозициональных переменных формулы, а число столбцов не меньше (n+m), где m – число логических связок в формуле.

Пример: В семье есть договоренность относительно пользования телевизором на субботние вечера: а) если не смотрит отец(⎤А), то смотрит дочь (C) и не смотрит мать (⎤В), т.е. F1=(⎤А→C∧⎤В);б) если не смотрит дочь (⎤C), то смотрит мать (В) и не смотрит отец (⎤А), т.е. F2=(⎤C→B∧⎤A); в) если смотрит отец (A), то не смотрит дочь (⎤C), т.е. F3=( A→⎤C).
В каком случае совместимы эти условия?
Формальная запись этого суждения имеет вид:
F=F1∧F2∧F3=(⎤А→C∧⎤В)∧(⎤C→B∧⎤A)∧(A→⎤C).
Анализ таблицы показывает, что эти условия совместимы, когда А=«Л», В=«Л» и С=«И».

Логическое следствие
Теорема . (признак логического следствия). Формула H будет логическим следствием формулы F тогда и только тогда, когда формула F → H является тавтологией

Логическое следствие
Определение. Формула B называется логическим следствием формул A1, A2, …,An если для всех наборов значений букв которые входят в A1, A2,…, An и B, значение есть И каждый раз, когда значение каждой формулы Ai на этом наборе есть И. Обозначается A1,A2,.,An ⟼B.

Аксиомы исчисления высказываний
Для полного набора логических связок: импликация, отрицание, конъюнкция и дизъюнкция система содержит десять аксиом. В силу полноты систем, использующих логические связки а) импликации и отрицания, б) импликации и дизъюнкции, в) импликации, отрицания, конъюнкции и дизъюнкции можно использовать в процессе дедуктивного вывода любую из указанных систем.

Определение исчисления высказываний, как и любой формальной системы, следует начинать с задания множества аксиом и правил вывода, обеспечивающих последовательное их использование при доказательстве истинности заключения.
Доказательством называют конечную последовательность высказываний, каждое из которых является либо аксиомой, либо выводится из одного или более предыдущих высказываний этой последовательности по правилам вывода.
Определение минимально возможного множества аксиом определяет семантическую полноту исчисления, а определение правил, обеспечивающих последовательное использование аксиом и промежуточных высказываний в процессе формирования заключения – метод дедуктивного вывода.

Аксиомы исчисления высказываний
Множество формул, удовлетворяющих условиям тождественной истинности, бесконечно. Однако в качестве аксиом всегда выбирают только такие, которые при истинности посылок обеспечивают дедуктивный вывод истинности заключения. При этом стремятся создать такую систему аксиом, которая содержала бы минимальное число формул для заданного набора логических связок. Так известна система, которая для логических связок импликации и отрицания содержит только три аксиомы, полная система аксиом, опирающаяся на две логические связки «¬» и «→», которая содержит три аксиомы:
• (F1→(F2→F1)),
• (F1→(F2→F3))→((F1→F2)→(F1→F3)),
• (¬F1→¬F2)→((¬F1→F2)→F1).

Аксиомы исчисления высказываний:
А1. F1→(F2→F1);
А2. (F1→F2)→((F2→F3))→(F1→F3));
А3. (F1∧ F2)→F1;
А4. (F1∧ F2)→F2; А5. F1→(F2→(F1∧F2));
А6. F1→(F1∨F2);
А7. F2→(F1∨F2);
А8. (F1→F3)→((F2→F3)→((F1∨F2)→F3));
А9. (F1→F2)→(( F1→⎤ F2)→⎤ F1);
A10. (F1→F2)→((F1∧F3)→(F2∧F3));
A11. (F1→ F2)→((F1∨F3)→(F2∨F3));
А12. ⎤⎤ F1 → F1.

Связь между алгеброй высказываний и исчислением высказываний.
Формулы исчисления высказываний можно интерпретировать как формулы алгебры высказываний. Для этого будем трактовать переменные исчисления высказываний как переменные алгебры высказываний, т. е. переменные в содержательном смысле, принимающие два значения: истина и ложь (1 и 0).
Операции определим так же, как в алгебре высказываний.
При этом всякая формула исчисления высказываний при любых входящих в нее переменных будет принимать одно из значений 1 или 0, вычисляемое по правилам алгебры высказываний. Введем понятие значения формулы исчисления высказываний. Пусть А- формула исчисления высказываний, х1,х2,…,хn- попарно различные переменные, среди которых находятся все переменные, входящие в формулу А. Обозначим через а1, а2,…,аn набор значений этих переменных, состоящих из 1 и 0, длины n. Очевидно, что вектор (а1, а2,…,аn) имеет 2n значений.
Имеют место три теоремы, которые устанавливают связь между основными фактами алгебры высказываний и исчисления высказываний.

Теорема 1.
Каждая формула, доказуемая в исчислении высказываний, является тождественно истинной в алгебре высказываний.
Формулировка этой теоремы содержит в себе три положения:
1)Каждая аксиома исчисления высказываний – тождественно истинная формула в алгебре высказываний.
2)Правило подстановки, примененное к тождественно истинным формулам, приводит к тождественно истинным формулам.
3)Правило заключения, примененное к тождественно истинным формулам, приводит к тождественно истинным формулам.