Слайд 8КАСП КАРДИОИДЫ
Касп (cusp — заострение) или точка возврата — точка, в которой кривая линия разделяется на

две (или более) ветви, имеющие в этой точке одинаковый направляющий вектор.
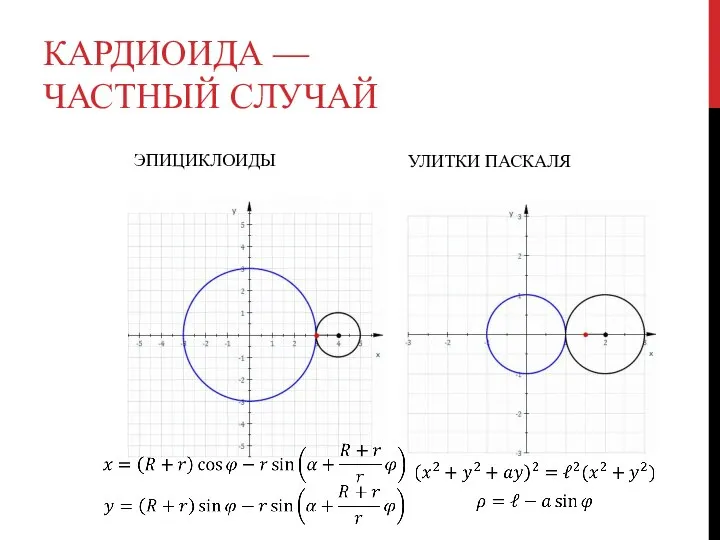
Слайд 9КАРДИОИДА — ЧАСТНЫЙ СЛУЧАЙ
ЭПИЦИКЛОИДЫ
УЛИТКИ ПАСКАЛЯ
Слайд 11СВОЙСТВА
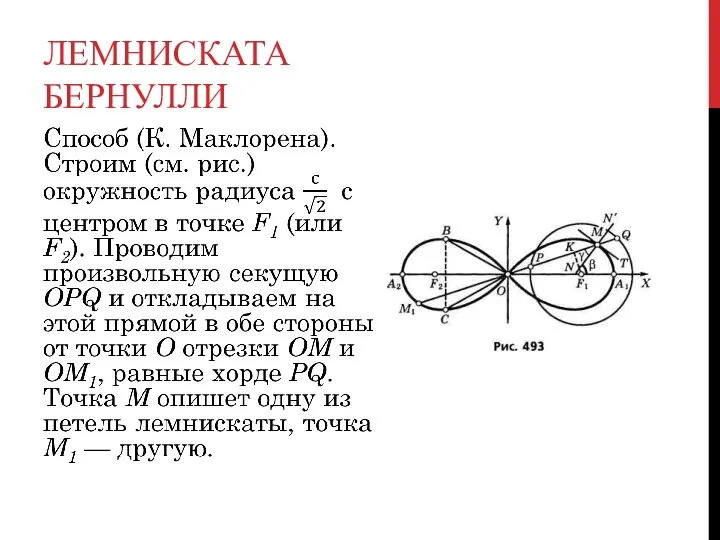
Кривая является геометрическим местом точек, симметричных центру равносторонней гиперболы относительно её касательных.

Отрезок биссектрисы угла между фокальными радиусами - векторами точки лемнискаты равен отрезку от центра лемнискаты до пересечения её оси с этой биссектрисой.
Материальная точка, движущаяся по лемнискате под действием однородного гравитационного поля, пробегает дугу за то же время, что и соответствующую хорду (см. рисунок). Предполагается, что ось лемнискаты составляет угол 45° вектором напряжённости поля, а центр лемнискаты совпадает с исходным положением движущейся точки.
Перпендикуляр, опущенный из фокуса лемнискаты на радиус-вектор какой-либо её точки, делит площадь соответствующего сектора пополам.
Слайд 12ЛЕМНИСКАТА БЕРНУЛЛИ — ЧАСТНЫЙ СЛУЧАЙ ОВАЛА КАССИНИ

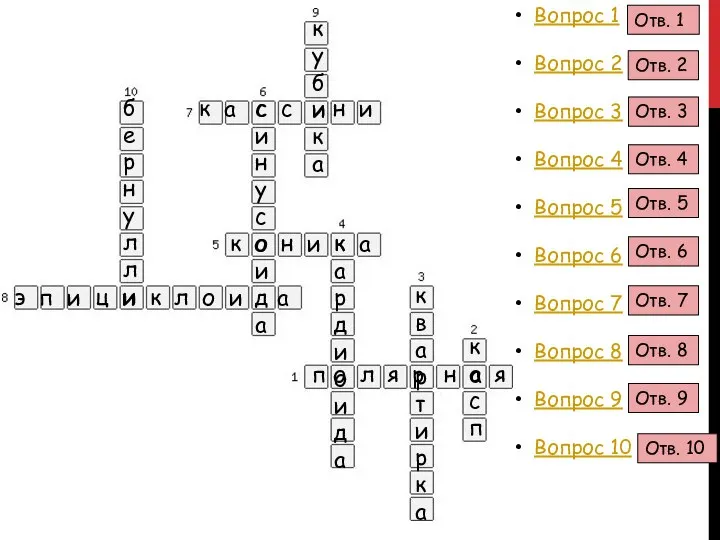
Слайд 13Вопрос 1
Вопрос 2
Вопрос 3
Вопрос 4
Вопрос 5
Вопрос 6
Вопрос 7
Вопрос 8
Вопрос 9
Вопрос 10
кубика
к а
с с и н и
к о н и к а
с инус
о
ида
бернулли
э п и ц и к л о и а
к
ардиоида
п о л я р н а я
ква
р
т
и
р
к
а
к
а
с
п
Отв. 1
Отв. 2
Отв. 3
Отв. 4
Отв. 5
Отв. 6
Отв. 7
Отв. 8
Отв. 9
Отв. 10
Слайд 15КАРДИОИДА
Даны: точка О (полюс), окружность К диаметра ОB = а, проходящая через

полюс (основная окружность; она показана на чертеже пунктиром).
Из полюса О проводим произвольную прямую ОР.
От точки Р, где прямая ОР вторично пересекает окружность, откладываем в обе стороны от Р отрезки РМ1 = РМ2 = a.
Геометрическое место точек M1, М2 (L на рис) называется кардиоидой.
Слайд 17ВОПРОС 1
Двухмерная система координат, в которой каждая точка на плоскости однозначно определяется

двумя числами — … углом и … радиусом.
<к кроссворду
Слайд 18ВОПРОС 2
Точка, в которой кривая линия разделяется на две (или более) ветви,

имеющие в этой точке одинаковый направляющий вектор.
<к кроссворду
Слайд 19ВОПРОС 3
Алгебраическая кривая степени n=4.
<к кроссворду

Слайд 20ВОПРОС 4
Плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности

с таким же радиусом.
<к кроссворду
Слайд 21ВОПРОС 5
Алгебраическая кривая степени n=2.
<к кроссворду

Слайд 22ВОПРОС 6
Плоская кривая задаваемая графиком функции y=sinx.
<к кроссворду

Слайд 23ВОПРОС 7
Лемниската Бернулли — частный случай овала .?.
<к кроссворду

Слайд 24ВОПРОС 8
Плоская кривая, образуемая фиксированной точкой окружности, катящейся по внешней стороне другой

окружности без скольжения.
<к кроссворду
Слайд 25ВОПРОС 9
Алгебраическая кривая степени n=3.
<к кроссворду






















 Векторы. 9 класс
Векторы. 9 класс Задачи для всех-всех-всех
Задачи для всех-всех-всех Алгебра. Лекция 3
Алгебра. Лекция 3 Решение тригонометрических уравнений. 10 класс
Решение тригонометрических уравнений. 10 класс Пифагор и его школа
Пифагор и его школа Логарифмические уравнения с параметром
Логарифмические уравнения с параметром Практика. Дискретная математика
Практика. Дискретная математика Признаки делимости чисел
Признаки делимости чисел Задачи по стереометрии. Подготовка к ЕГЭ
Задачи по стереометрии. Подготовка к ЕГЭ Дифференциальные уравнения и их применение в медицине
Дифференциальные уравнения и их применение в медицине Приемы решения экономических задач в ЕГЭ
Приемы решения экономических задач в ЕГЭ Геометрические фигуры (интерактивная игра)
Геометрические фигуры (интерактивная игра) Теорема, обратная теореме Пифагора
Теорема, обратная теореме Пифагора Графическое представление газовых законов
Графическое представление газовых законов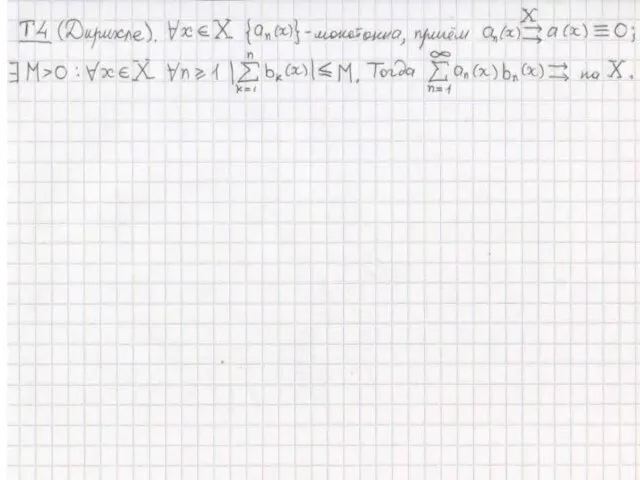 Свойства равномерно-сходящихся плоскостей и рядов
Свойства равномерно-сходящихся плоскостей и рядов Презентация на тему Скалярное произведение векторов (9 класс)
Презентация на тему Скалярное произведение векторов (9 класс)  Множества и его элементы
Множества и его элементы Правильные многоугольники. Геометрия
Правильные многоугольники. Геометрия Вектор Вектор – отрезок, для которого указано, какой из его концов считается началом, а какой – концом.
Вектор Вектор – отрезок, для которого указано, какой из его концов считается началом, а какой – концом. Математический анализ. Неопределенный интеграл
Математический анализ. Неопределенный интеграл Юбилейный ЕГЭ по математике Вперед! Только вперед!
Юбилейный ЕГЭ по математике Вперед! Только вперед! d694e47421834013895052f206be4c31
d694e47421834013895052f206be4c31 Умножение на 2. Проведите динозаврика по лабиринту (2)
Умножение на 2. Проведите динозаврика по лабиринту (2) Решение неравенств с одной переменной
Решение неравенств с одной переменной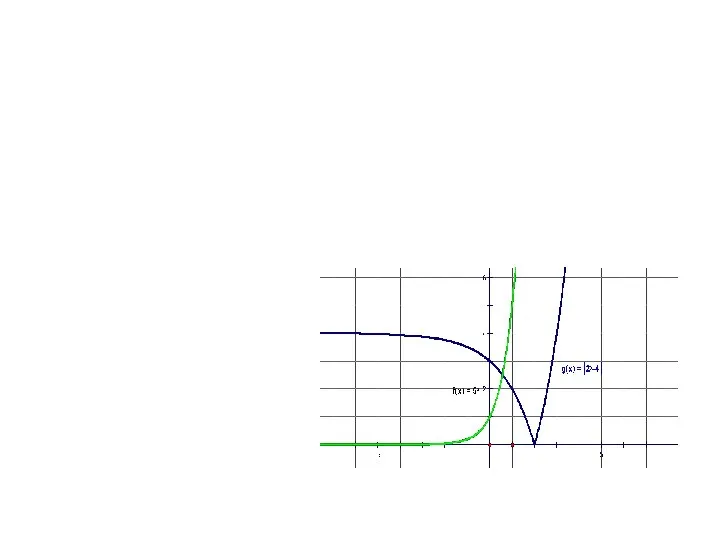 Показательные уравнения
Показательные уравнения ИПАР по математике. Задача на проценты. Тема: математика в профессии моих родителей
ИПАР по математике. Задача на проценты. Тема: математика в профессии моих родителей Числовые неравенства и их свойства. Подготовка к ОГЭ
Числовые неравенства и их свойства. Подготовка к ОГЭ Решение уравнений производная
Решение уравнений производная