- Главная
- Математика
- Доказательство формулы сокращённого умножения (а b) (a b) a b другим способом

Содержание
Слайд 3 Каким же способом доказывали эту формулу наши предки?
А как они
Каким же способом доказывали эту формулу наши предки?
А как они

это делали, мы сейчас покажем.
Возьмём прямоугольник со сторонами (а + в) и (а – в)
Его площадь равна (а + в)·(а – в) (рис. 1.).
Этот прямоугольник разрежем на два прямоугольника со сторонами в и (а – в) и а и (а – в). Теперь эти прямоугольники приложим, друг к другу, как показано на рис. 2.
Достроим получившуюся фигуру до квадрата со стороной а. Чтобы узнать площадь исходного прямоугольника, надо из площади квадрата со стороной а вычесть площадь квадрата со стороной в. Итак, формула сокращённого умножения
(а + в)·(а - в) = а2-в2 доказана геометрическим способом.
Возьмём прямоугольник со сторонами (а + в) и (а – в)
Его площадь равна (а + в)·(а – в) (рис. 1.).
Этот прямоугольник разрежем на два прямоугольника со сторонами в и (а – в) и а и (а – в). Теперь эти прямоугольники приложим, друг к другу, как показано на рис. 2.
Достроим получившуюся фигуру до квадрата со стороной а. Чтобы узнать площадь исходного прямоугольника, надо из площади квадрата со стороной а вычесть площадь квадрата со стороной в. Итак, формула сокращённого умножения
(а + в)·(а - в) = а2-в2 доказана геометрическим способом.
рис. 1
рис. 2
- Предыдущая
Картины Ван Гога (постимпрессионизм)Следующая -
Решение логических задач табличным способом
 Площади многоугольников
Площади многоугольников Сложение и вычитание вида +- 1
Сложение и вычитание вида +- 1 Роль и место математики в современном мире. Пределы, их свойства (лекция 1)
Роль и место математики в современном мире. Пределы, их свойства (лекция 1) Случаи вычитания 11 -
Случаи вычитания 11 -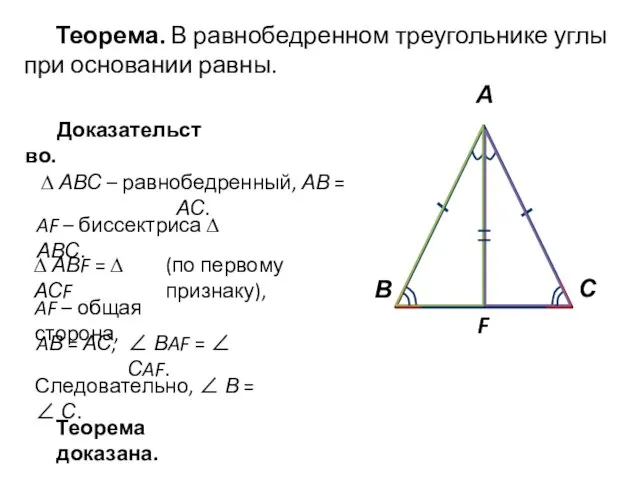 Теоремы к зачёту
Теоремы к зачёту Решение текстовых задач
Решение текстовых задач Рабочая книга – инструмент анализа временных рядов
Рабочая книга – инструмент анализа временных рядов Презентация на тему Преобразование графиков. Тригонометрические функции. Алгебра и начала анализа. 10 класс
Презентация на тему Преобразование графиков. Тригонометрические функции. Алгебра и начала анализа. 10 класс  Понятие функции
Понятие функции Проценты
Проценты Первый урок математики в 6 классе - Презентация
Первый урок математики в 6 классе - Презентация Построение косинуса
Построение косинуса Решение задач на оптимизацию методами математического анализа
Решение задач на оптимизацию методами математического анализа Страницы истории города Омска в задачах
Страницы истории города Омска в задачах Виды треугольников по видам углов
Виды треугольников по видам углов Формулы тригонометрии
Формулы тригонометрии Алгоритм решения уравнений
Алгоритм решения уравнений Пропорции
Пропорции Тренировка интеллекта
Тренировка интеллекта Эллипс
Эллипс Великолепная алгебра и занимательная геометрия
Великолепная алгебра и занимательная геометрия Цифра 1. Посчитаем до 10
Цифра 1. Посчитаем до 10 Старинные задачи на дроби
Старинные задачи на дроби Производная в ЕГЭ
Производная в ЕГЭ Актуализация знаний
Актуализация знаний Практическое применение производных
Практическое применение производных Наиболее распространенные задачи математической статистики
Наиболее распространенные задачи математической статистики Видовые числа и коэффициенты формы стволов деревьев
Видовые числа и коэффициенты формы стволов деревьев