Основы эконометрического моделирования

План:
1. Предмет эконометрики
2. Основные понятия
3. Определение вероятности события

Предмет эконометрики
Эконометрика – наука, исследующая количественные закономерности и взаимозависимости в экономике при помощи методов математической статистики

Основные задачи статистического анализа
Выявление наличия или отсутствия взаимосвязи между изучаемыми факторами (корреляционный анализ)
Определение вида взаимосвязи между изучаемыми факторами (регрессионный анализ)
Проверка гипотезы о виде взаимосвязи между факторами

Основные понятия
Достоверным называют событие, которое при осуществлении совокупности условий обязательно произойдет
Невозможным называют событие, которое при осуществлении совокупности условий заведомо не произойдет

Основные понятия
Случайным называют событие, которое при осуществлении совокупности условий может либо произойти, либо не произойти
События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании

Основные понятия
События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое
Каждый из возможных результатов испытания называется элементарным событием

Полная группа событий
События образуют полную группу, если в результате испытания обязательно произойдет хотя бы одно из этих событий

Классическое определение вероятности
Вероятность события А определяется формулой
P(A) = m/n,
где m – число элементарных событий, благоприятствующих событию А, n – число всевозможных элементарных событий (при этом предполагается, что элементарные события являются несовместными, равновозможными и образуют полную группу событий)
Вероятность события удовлетворяет двойному неравенству
0 ≤ P(A) ≤ 1

Пример
Вычислить следующие вероятности:
P( W > 60 kg) = 12/20 = 0,6
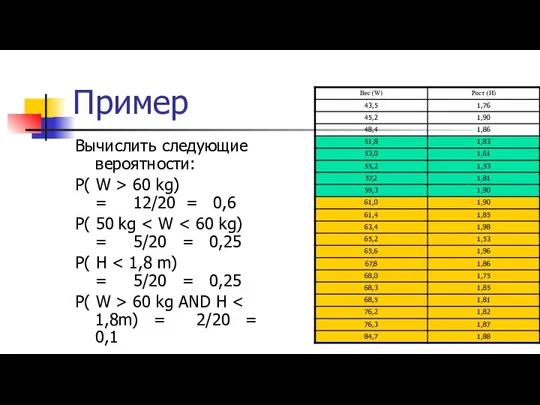
P( 50 kg < W < 60 kg) = 5/20 = 0,25
P( H < 1,8 m) = 5/20 = 0,25
P( W > 60 kg AND H < 1,8m) = 2/20 = 0,1

Относительная частота
Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически проведенных испытаний:
W(A) = m/n ,
где m – число появлений события, n – общее число испытаний.
Относительную частоту принимают в качестве статистической вероятности события

Недостатки классического определения
число элементарных исходов испытания не всегда является ко­нечным
часто невозможно представить результат испытания в виде совокупности элементарных событий
не всегда можно указать основания, позволяющие считать элементарные события равновозможными

Геометрическая вероятность
Пусть отрезок l составляет часть отрезка L. На отре­зок L наудачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относи­тельно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством
Р = Длина l/Длина L

Геометрическая вероятность
Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Это означает выполнение следующих предположений: брошен­ная точка может оказаться в любой точке фигуры G, вероятность попадания брошенной точки на фигуру g пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы g. В этих предположениях вероятность попадания точки в фигуру g определяется равенством
Р = Площадь g / Площадь G

Пример
На плоскости начерчены две концентрические окруж­ности, радиусы которых r = 5 и R = 10 см соответственно. Найти вероят­ность того, что точка, брошенная наудачу в большой круг, попадет в маленький круг.
Решение: По определению геометрической вероятности
p = s/S = 25/100 = 0,25

Задание
Скачать файл «Практическое занятие 1» из MOODLE и выполнить приведенные задания
Решение задания загрузить в MOODLE