Содержание
- 2. Соболевская Елена Павловна доцент кафедры дискретной математики и алгоритмики, кандидат физико-математических наук, доцент Лауреат премии имени
- 3. Буславский Александр Андреевич старший преподаватель кафедры дискретной математики и алгоритмики, Лауреат специального фонда Президента Республики Беларусь
- 4. Информационно-коммуникационные технологии: Образовательный портал БГУ https://edufpmi.bsu.by Образовательная платформа Insight Runner https://acm.bsu.by/ Группы в мессенджере Telegram, сервисы
- 5. Соболь Сергей Александрович инженер-программист ООО ЯндексБел, старший преподаватель кафедры дискретной математики и алгоритмики (2014-2020 год), магистр
- 6. Insight Runner ФПМИ БГУ https://acm.bsu.by/ логин номер вашего студенческого (семь цифр) пароль (по умолчанию): 11111 После
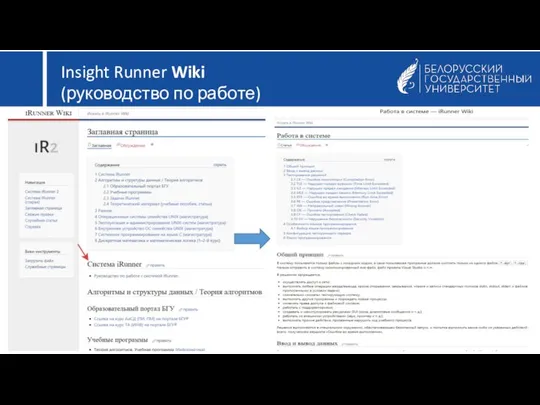
- 7. Insight Runner Wiki (руководство по работе)
- 8. ФПМИ БГУ Insight Runner Wiki
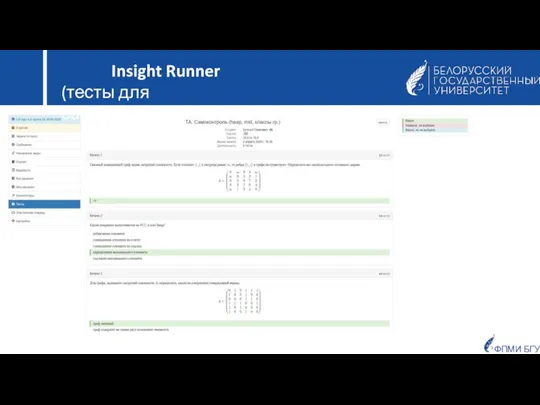
- 9. ФПМИ БГУ Для самоконтроля усвоения теоретического материала в Insight Runner разработана система тестов. Тесты разработаны для
- 10. ФПМИ БГУ Insight Runner (тесты для самоконтроля)
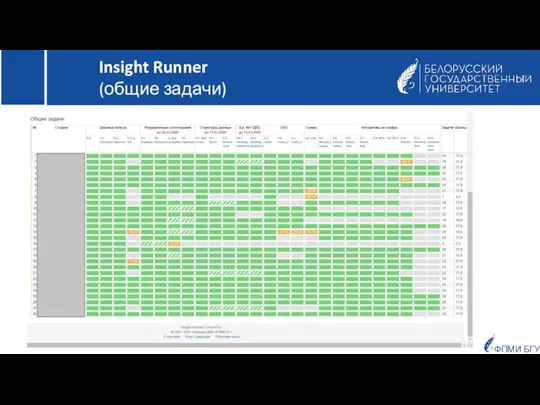
- 11. ФПМИ БГУ Для закрепления на практике теоретических знаний в Insight Runner разработаны общие задачи (их должны
- 12. ФПМИ БГУ Тема 1. Бинарные поисковые деревья: 0.1 построение дерева 0.2 удаление вершин из дерева 0.3
- 13. ФПМИ БГУ Insight Runner (общие задачи)
- 14. ФПМИ БГУ В рамках учебной дисциплины студентами также выполняются индивидуальные задачи. Число индивидуальных задач - по
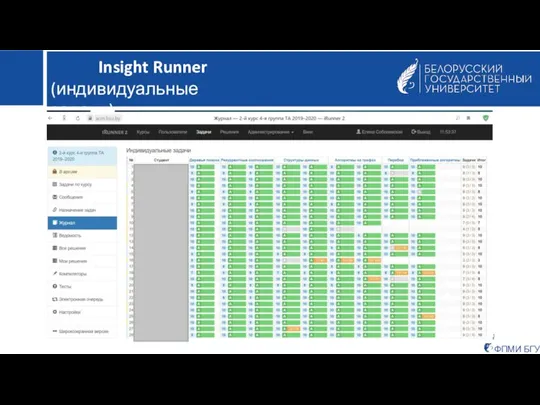
- 15. ФПМИ БГУ Insight Runner (индивидуальные задачи)
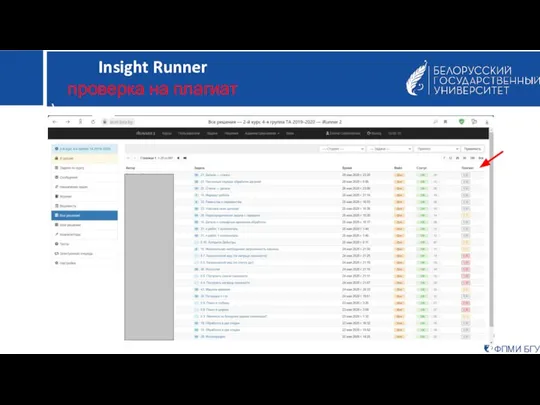
- 16. ФПМИ БГУ Insight Runner проверка на плагиат )
- 17. ФПМИ БГУ Insight Runner проверка на плагиат
- 18. ФПМИ БГУ В.М. Котов, Е. П. Соболевская, А. А. Толстиков. «Алгоритмы и структуры данных»: учеб. пособие
- 19. Для выполнения первой индивидуальной задачи, необходимо обладать навыками работы с бинарными поисковыми деревьями. Частично вы уже
- 20. Словарные операции поиск элемента с заданным ключом х добавление нового элемента с заданным ключом х удаление
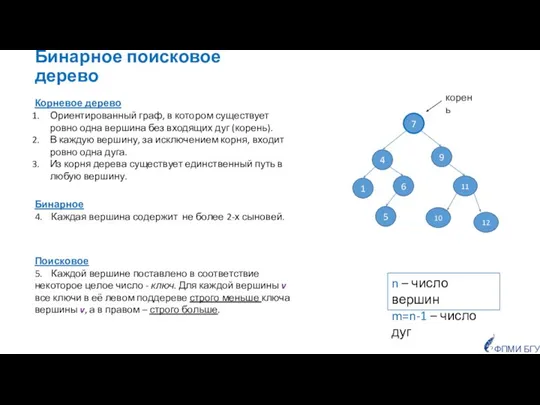
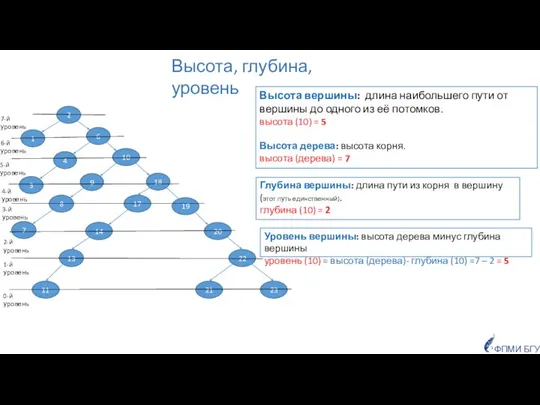
- 21. Бинарное поисковое дерево Поисковое 5. Каждой вершине поставлено в соответствие некоторое целое число - ключ. Для
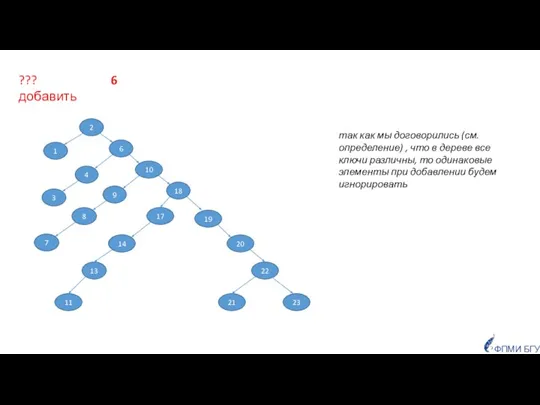
- 22. 10 18 23 21 22 20 19 11 13 14 17 3 4 6 8 9
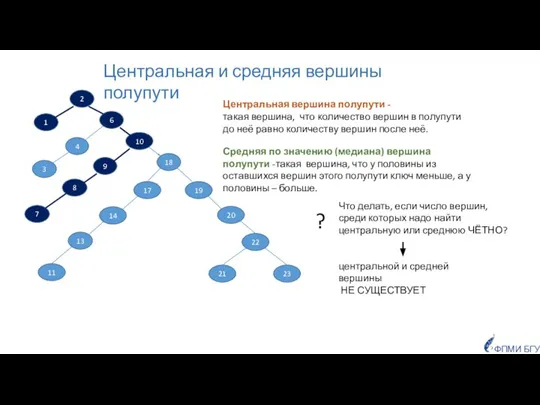
- 23. 10 18 23 21 22 20 19 11 13 14 17 3 4 6 8 9
- 24. 10 18 23 21 22 20 19 11 13 14 17 3 4 6 8 9
- 25. 10 18 23 21 22 20 19 11 13 14 17 3 4 6 8 9
- 26. 10 18 23 21 22 20 19 11 13 14 17 3 4 6 8 9
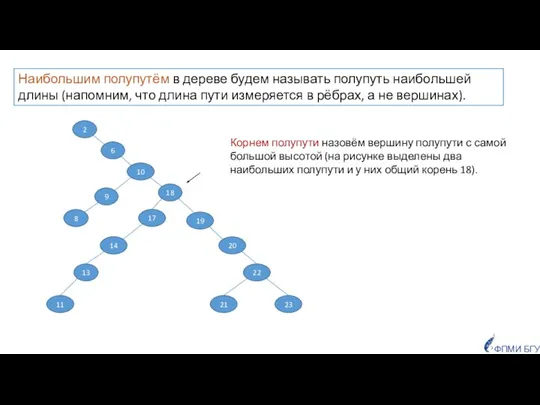
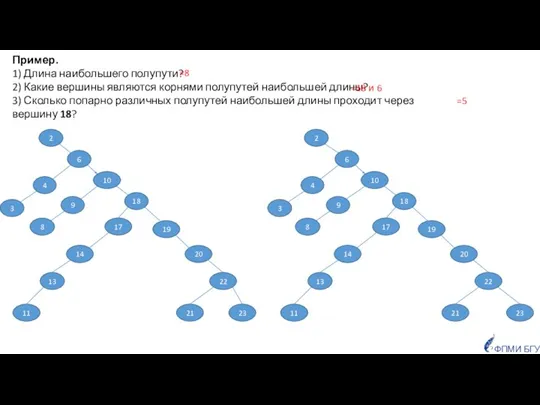
- 27. 10 18 23 21 22 20 19 11 13 14 17 6 8 9 2 Наибольшим
- 28. 10 18 23 21 22 20 19 11 13 14 17 3 4 6 8 9
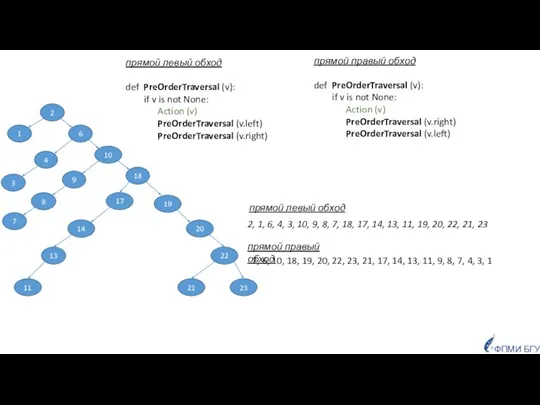
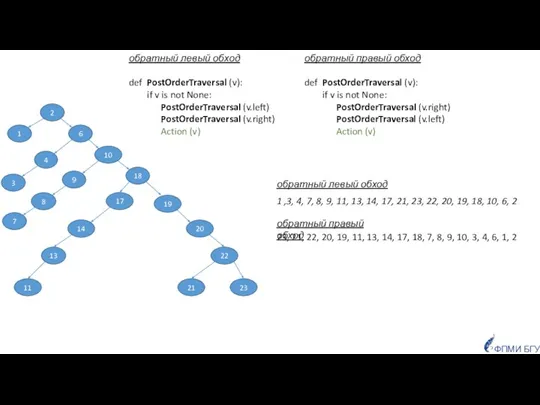
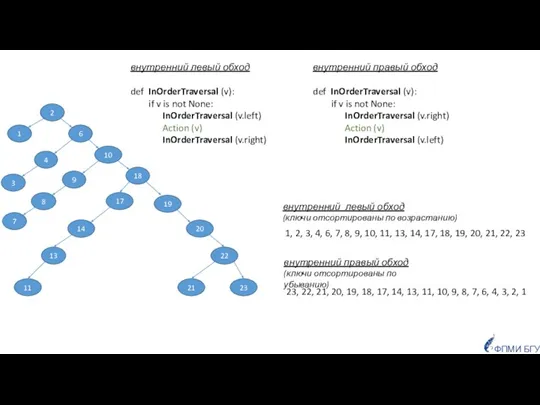
- 29. прямой (левый, правый) - PreOrderTraversal (v) ФПМИ БГУ Обходы обратный (левый, правый) - PostOrderTraversal (v) внутренний
- 30. 10 18 23 21 22 20 19 11 13 14 17 3 4 6 8 9
- 31. 10 18 23 21 22 20 19 11 13 14 17 3 4 6 8 9
- 32. 10 18 23 21 22 20 19 11 13 14 17 3 4 6 8 9
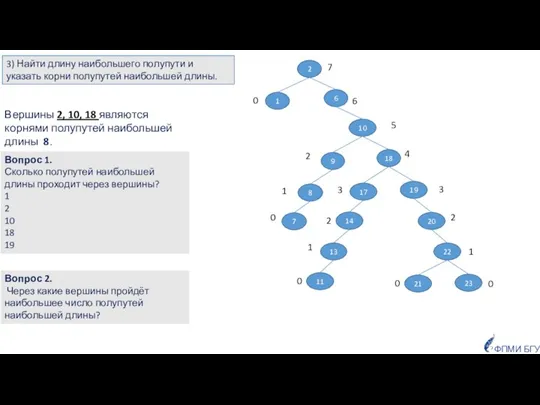
- 33. ФПМИ БГУ Примеры задач Найти высоту дерева. Определить, является ли дерево сбалансированнным по высоте. Найти длину
- 34. Обратный левый (или правый) обход если вершина v лист, то её высота равна 0; если у
- 35. 10 18 23 21 22 20 19 11 13 14 17 6 8 9 2 0
- 36. 10 18 23 21 22 20 19 11 13 14 17 6 8 9 2 0
- 37. если вершина v лист, то её метка равна 1; если у вершины v только одно поддерево,
- 38. Выполнить любой обход дерева и подсчитать число вершин (n=15). Если n – чётно, то полагаем, что
- 39. Сначала обратным обходом расставить вершинам метки высот. Во время этого же обхода подсчитать количество вершин, у
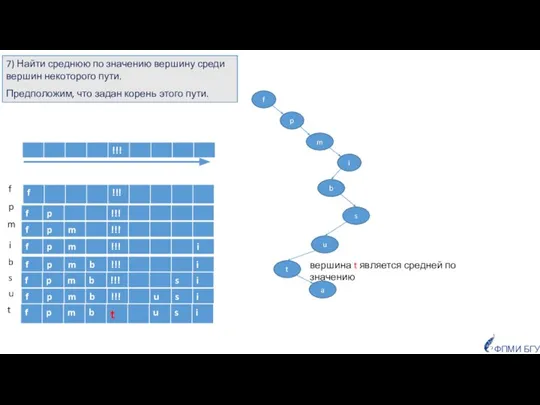
- 40. m i a t u s b p f вершина t является средней по значению f
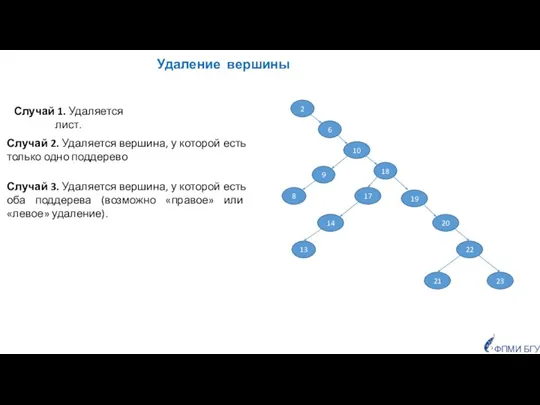
- 41. Удаление вершины ФПМИ БГУ Случай 1. Удаляется лист. Случай 2. Удаляется вершина, у которой есть только
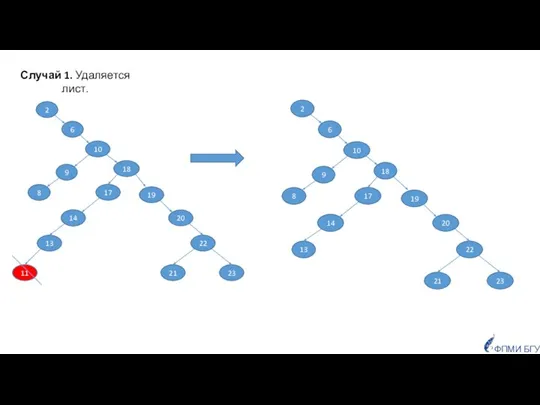
- 42. ФПМИ БГУ Случай 1. Удаляется лист.
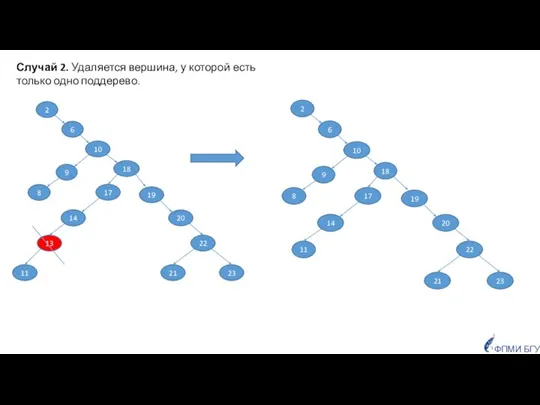
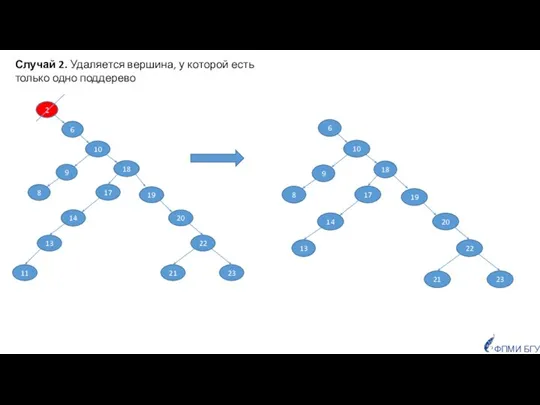
- 43. ФПМИ БГУ Случай 2. Удаляется вершина, у которой есть только одно поддерево.
- 44. ФПМИ БГУ Случай 2. Удаляется вершина, у которой есть только одно поддерево
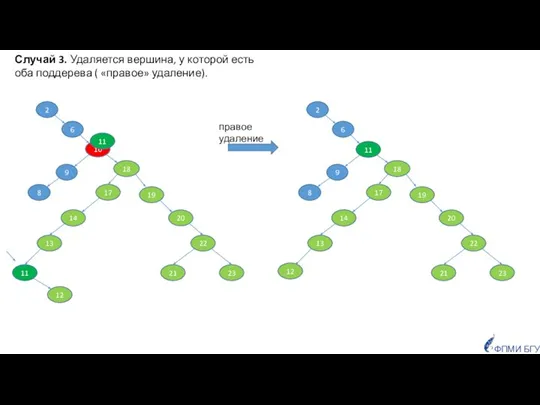
- 45. 10 18 23 21 22 20 19 11 13 14 17 6 8 9 2 правое
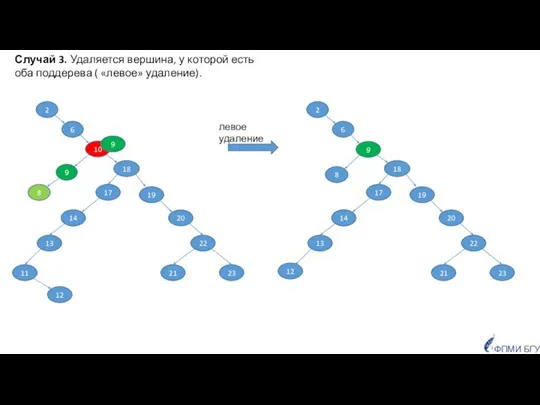
- 46. 10 18 23 21 22 20 19 11 13 14 17 6 8 9 2 левое
- 47. !!! Если у удаляемой вершины только одно поддерево, то НЕТ ПОНЯТИЯ ПРАВОЕ/ЛЕВОЕ удаление. Удаление всегда выполняется
- 48. Оценки числа операций в худшем случае 10 18 19 6 2 построение дерева для последовательности из
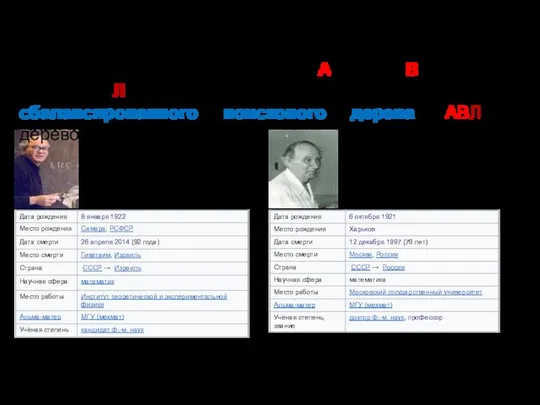
- 49. Георгий Максимович Адельсон-Вельский Евгений Михайлович Ландис В 1962 году советские учёные Г.М. Адельсон-Вельский и Е.М. Ландис
- 50. ФПМИ БГУ В рамках дисциплины мы подробно исследуем эту структуру данных, а пока - краткая информация
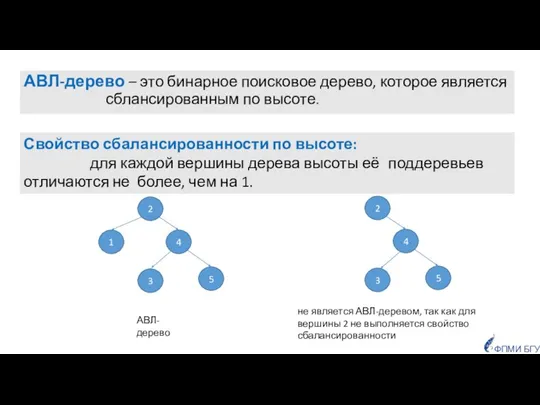
- 51. АВЛ-дерево – это бинарное поисковое дерево, которое является сблансированным по высоте. 2 4 1 3 5
- 52. ТЕОРЕМА. Пусть n – число внутренних вершин АВЛ-дерева, а h – его высота. Тогда справедливы следующие
- 53. Использование поисковых деревьев на практике ФПМИ БГУ
- 54. Сортировка деревом 1. По последовательности чисел сначала построим АВЛ-дерево последовательным добавлением элемента. n*log n 2. Выполним
- 55. Абстрактный тип данных: множество (set) Множество (англ. set) —хранит набор попарно различных объектов без определённого порядка.
- 56. Абстрактный тип данных ассоциативный массив (map) Ассоциативный массив (англ. associative array), или отображение (англ. map), или
- 57. Сборник задач по теории алгоритмов : учеб.-метод. пособие / В.М. Котов, Ю.Л. Орлович, Е.П. Соболевская, С.А.
- 59. Скачать презентацию































 Кривые Безье
Кривые Безье 11.10
11.10 Вычисления и преобразования
Вычисления и преобразования Рівняння дотичної до графіка функції
Рівняння дотичної до графіка функції Тригонометрия. Графики
Тригонометрия. Графики Нахождение числа по его дроби
Нахождение числа по его дроби Решение тригонометрических неравенств
Решение тригонометрических неравенств В мире плоскостей
В мире плоскостей Золотое сечение. Витрувий
Золотое сечение. Витрувий Косинус угла
Косинус угла Римские цифры
Римские цифры Опрос общественного мнения. Повторение действий с дробями
Опрос общественного мнения. Повторение действий с дробями Математика.Управление социальными системами. Математический анализ. Функции. Пределы. Непрерывность
Математика.Управление социальными системами. Математический анализ. Функции. Пределы. Непрерывность Площадь прямоугольника
Площадь прямоугольника Research Topics for Mathematics II
Research Topics for Mathematics II Презентация на тему ЗАДАЧИ НА ЧАСТИ
Презентация на тему ЗАДАЧИ НА ЧАСТИ  Логарифмы. Свойства логарифмов
Логарифмы. Свойства логарифмов Презентация на тему Разность квадратов
Презентация на тему Разность квадратов  Решение линейных уравнений с одной переменной
Решение линейных уравнений с одной переменной Презентация на тему Решение иррациональных уравнений
Презентация на тему Решение иррациональных уравнений  Умножение одночлена на многочлен
Умножение одночлена на многочлен Признак параллелограма
Признак параллелограма Тренажёр. Полёт бабочки. (1 класс)
Тренажёр. Полёт бабочки. (1 класс) Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения Решение тригонометрических уравнений. 10 класс
Решение тригонометрических уравнений. 10 класс Изображение десятичной дроби на координатном луче
Изображение десятичной дроби на координатном луче двугранные углы(1)
двугранные углы(1) Производная функция
Производная функция