Аналитическая геометрия на плоскости Лекция 1-2

Основные задачи метода координат

Прямоугольная система координат
Определение: Прямоугольной (декартовой) системой координат на плоскости называется две взаимно перпендикулярные оси Ох и Оу, имеющие общее начало О и одинаковую масштабную единицу.
Ох называется осью абсцисс, Оу – осью ординат. Из произвольной точки М опустим перпендикуляры на оси Ох и Оу.

Число х называется абсциссой, у – ординатой точки М. Упорядоченная пара (х; у) называется координатами точки М.
Каждой точке на плоскости в прямоугольной системе координат соответствует единственная пара действительных чисел (х; у).
Метод определения положения точек на плоскости с помощью чисел называется методом координат.

Расстояние от точки М(х; у) до начала координат определяется по формуле: (1)
Теорема: Для любых двух точек М1(х1; у1) и М2(х2; у2)
на плоскости расстояние между ними выражается
формулой: (2)

Пример: Даны точки . Найти расстояние между этими точками.
Решение:
Используя формулу (2) получим:

Деление отрезка в данном отношении
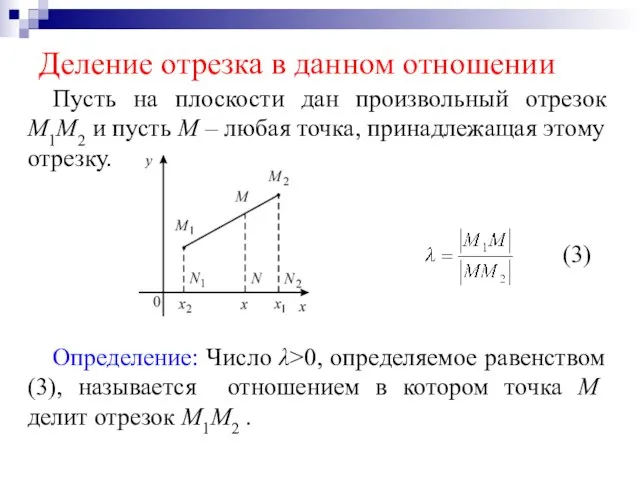
Пусть на плоскости дан произвольный отрезок М1М2 и пусть М – любая точка, принадлежащая этому отрезку.
(3)
Определение: Число λ>0, определяемое равенством (3), называется отношением в котором точка М делит отрезок М1М2 .

Задача о делении отрезка в данном отношении состоит в том, чтобы по данному отношению λ и координатам точек М1 и М2 найти координаты точки М.
Теорема: Если точка М делит отрезок М1М2 в отношении λ, то координаты этой точки определяются по формулам:
(4)
где (х1; у1) – координаты точки М1 ,
(х2; у2) – координаты точки М2 .

Следствие: Если точка М делит отрезок М1М2 пополам, то есть ( ), то координаты этой точки определяются по формулам:
(5)

Пример: Даны точки М1(1; 1) и М2(7; 4). Найти точку М, которая в два раза ближе к М1, чем к М2.
Решение:
Искомая точка делит отрезок в отношении
Применяя формулы (4), получим:
Следовательно, М(3; 2).

Полярная система координат
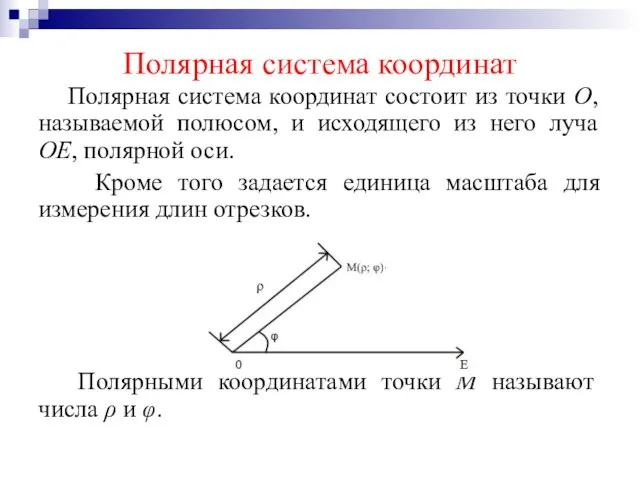
Полярная система координат состоит из точки О, называемой полюсом, и исходящего из него луча ОЕ, полярной оси.
Кроме того задается единица масштаба для измерения длин отрезков.
Полярными координатами точки М называют числа ρ и φ.

Установим связь между прямоугольными и полярными координатами точки.
Для этого совместим начало прямоугольной и полярной систем координат, а ось направим по направлению полярной оси ОЕ. Пусть точка М имеет прямоугольные координаты (х; у), полярные (ρ; φ).

Тогда из прямоугольного треугольника ONM получим:
(6)
(7)
(6) - выражает прямоугольные координаты через полярные.
(7) - выражает полярные координаты через прямоугольные.

Пример: Найти полярные координаты точки
Решение:
Воспользуемся формулами (7):
Так как точка лежит в четвертой четверти, то угол выбираем исходя из этого условия: или ,
то есть или .

Пример: Найти прямоугольные координаты точки
Решение:
Воспользуемся формулами (6):
Таким образом, прямоугольные координаты данной точки имеют вид:

Уравнение прямой на плоскости

Уравнение прямой с угловым коэффициентом
Определение: Углом наклона прямой, образованным с положительным направлением оси Ох называется наименьший угол α, на который нужно повернуть положительное направление оси Ох против хода часовой стрелки для совмещения ее с прямой.
Определение: Угловым коэффициентом прямой называется тангенс угла наклона прямой: (1)
Если то прямая параллельна оси Ох и
Если то прямая перпендикулярна оси Ох и говорят, что угловой коэффициент обращается в ∞ .

Выведем уравнение прямой, если ее положение определено величиной отрезка отсекаемого на оси Оу и угловым коэффициентом
Пусть М(х; у) – текущая точка искомой прямой.
Опустим перпендикуляр из точки М на ось Ох и через точку В проведем прямую, параллельно оси Ох.
Рассмотрим прямоугольный треугольник: .

Из треугольника: но
(2)
(2) – уравнение прямой с угловым коэффициентом.
При прямая образует с осью Ох острый угол, при – тупой, при прямая параллельна оси Ох.
При прямая пересекает ось Оу выше начала координат , при – ниже, при проходит через начало координат.

Уравнение прямой, проходящей через данную точку в заданном направлении
Выведем уравнение прямой, если ее положение определяется данной точкой М1(х1; у1) и заданным угловым коэффициентом
Запишем уравнение прямой в виде , где b – неизвестное число.
Так как прямая проходит через точку М1(х1; у1), то ее координаты удовлетворяют уравнению:
Отсюда подставляя в уравнение получим: или (3)

(3) – уравнение прямой, проходящей через данную точку в заданном направлении.
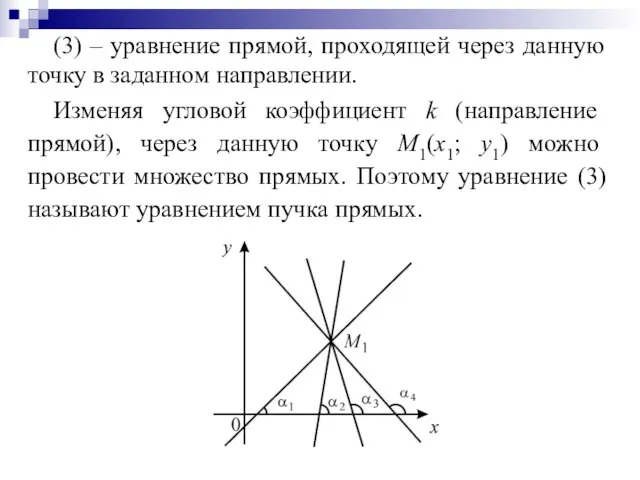
Изменяя угловой коэффициент k (направление прямой), через данную точку М1(х1; у1) можно провести множество прямых. Поэтому уравнение (3) называют уравнением пучка прямых.

Уравнение прямой, проходящей через две данные точки
Пусть положение прямой определяется двумя данными точками М1(х1; у1) и М2(х2; у2).
Запишем уравнение прямой в виде:
где k – неизвестное число.

Но прямая проходит через точку М2(х2; у2). Следовательно, координаты этой точки также удовлетворяют уравнению:
Откуда
Подставим найденный коэффициент в уравнение пучка прямых:
Перегруппируем левую правую часть и получим:
(4)
(4) – уравнение прямой проходящей через две данные точки.

Если х1=х2 , то уравнение прямой имеет вид: х=х1, и прямая параллельна оси Оу.
Если у1=у2 , то уравнение прямой имеет вид: у=у1, и прямая параллельна оси Ох.

Пример: Составить уравнение прямой, проходящей через точки М1(2; 3) и М2(3; –1).
Решение:
Воспользуемся формулой (4):
Разрешим полученное уравнение относительно у:
или

Пример: Составить уравнение прямой, проходящей через точки и
Решение:
Воспользуемся формулой (4):
На ноль делить нельзя, но можно воспользоваться свойством пропорции:
или
В данном примере поэтому можно было сразу записать уравнение прямой в виде:

Общее уравнение прямой
Теорема: В прямоугольной системе координат любая прямая задается уравнением первой степени:
(5)
где А и В одновременно не обращаются в ноль.
(5) называют общим уравнением прямой, так как данное уравнение охватывает все случае положения прямой на плоскости.
Из него можно получить другие уравнения прямой.

Уравнение прямой «в отрезках»
Рассмотрим общее уравнение прямой:
при условии, что все коэффициенты отличны от нуля.
Преобразуем его, для этого свободное слагаемое перенесем в правую часть и поделим левую и правую часть на –С :

Введем обозначение:
Тогда уравнение прямой примет вид:
(6)
(6) – уравнение прямой «в отрезках».
Замечание: в виде уравнения (6) не могут быть записаны уравнение прямой, проходящей через начало координат и уравнения прямых, параллельных осям координат.

Геометрический смысл уравнения (6) состоит в том, что числа и являются величинами отрезков, которые прямая отсекает на соответствующих осях координат.
Эта форма уравнения удобна для геометрического построения прямой.

Пример: Прямая задана уравнением
По данному уравнению прямой составить уравнение прямой «в отрезках» и построить прямую.
Решение:
Преобразуем уравнение прямой:
Отложим на осях Ох и Оу отрезки и проведем прямую через точки и

Угол между двумя прямыми
Пусть заданы прямые L1 и L2 уравнениями:
и , где
При пересечении двух прямых L1 и L2 на плоскости образуются четыре угла, которые попарно равны между собой как вертикальные углы.

Определим угол между прямыми:
Тогда
Так как , то отсюда следует, что (7)
(7) – определяет один из углов между двумя прямыми.
Второй угол равен π –φ.

Пример: Две прямые заданы уравнениями:
. Найти угол между этими прямыми.
Решение:
Воспользуемся формулой (7):
Так как то
Отсюда
Знак «–» указывает на то, что отсчет от первой прямой ко второй совершался по ходу часовой стрелки.

Условия параллельности и перпендикулярности двух прямых
Если прямые L1 и L2 параллельны, то и
то есть или (8)
(8) – условие параллельности двух прямых.

Условия параллельности и перпендикулярности двух прямых
Если прямые L1 и L2 перпендикулярны, то
то есть
(9)
(9) – условие перпендикулярности двух прямых.

Расстояние от точки до прямой
Пусть на плоскости Оху задана прямая L общим уравнением
Требуется найти расстояние от точки М0(х0; у0) до прямой L. Под расстоянием от точки до прямой понимают длину перпендикуляра, опускаемого из точки на прямую.
(10)
(10) – формула расстояния от точки М0 до прямой L.

Пример: Определить расстояние от точки
до прямой
Решение:
Воспользуемся формулой (10):
Приведем уравнение прямой к общему виду, для этого умножим уравнение на 3 и все перенесем в левую часть:

Кривые второго порядка

Окружность
Определение: Окружностью называется множество всех точек плоскости, равноудаленных от данной точки (центра окружности).
Если центр окружности совпадает с началом координат, то ее уравнение имеет вид:
(1)

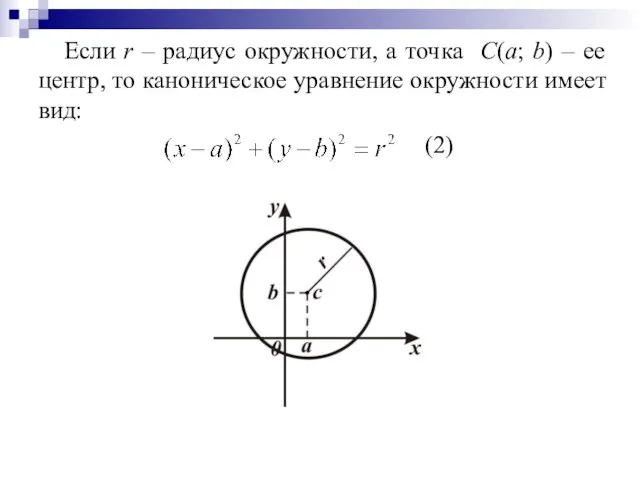
Если r – радиус окружности, а точка С(a; b) – ее центр, то каноническое уравнение окружности имеет вид:
(2)

Эллипс
Определение: Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между двумя фокусами.

По определению и, следовательно, или . Каноническое уравнение эллипса имеет вид:
(3)
где (4) , a – длина большой полуоси эллипса, b – длина малой полуоси эллипса ( ), с – половина расстояния между фокусами.
Оси координат являются осями симметрии эллипса.

– длина большой оси эллипса,
– длина малой оси эллипса,
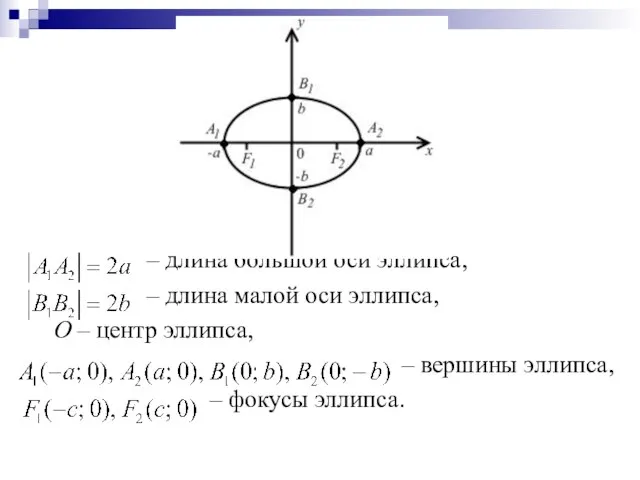
О – центр эллипса,
– вершины эллипса,
– фокусы эллипса.

Определение: Эксцентриситетом эллипса называется отношение половины расстояния между фокусами к длине большой полуоси эллипса: (5).
Так как , то .
Чем больше эксцентриситет, тем больше расстояние от центра эллипса до его фокусов и тем более «сплющен» эллипс; чем ближе эксцентриситет к 0, тем больше форма эллипса приближается к окружности.
При эллипс преобразуется в окружность, тогда и, следовательно, . Если , эллипс преобразуется в свою сдвоенную большую ось.

При эллипс расположен вдоль оси Оу. В этом случае оси Ох и Оу поменялись местами: большая ось и фокусы такого эллипса лежат на оси Оу, а малая ось на оси Ох.
Для такого эллипса:
– координаты фокусов;

Гипербола
Определение: Гиперболой называется множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между двумя фокусами.

По определению и, следовательно, или . Каноническое уравнение гиперболы имеет вид:
(6)
где (7) , a – длина действительной полуоси гиперболы, b – длина мнимой полуоси гиперболы, с – половина расстояния между фокусами.

Для построения гиперболы необходимо сначала построить осевой прямоугольник, затем провести диагонали этого прямоугольника, которые являются асимптотами гиперболы.
В силу симметрии гиперболы, она имеет две асимптоты: . Наличие асимптот и симметрии позволяют построить всю гиперболу.
Кривая состоит из двух не смыкающихся ветвей, лежащих в углах между асимптотами (8), и неограниченно приближающихся к этим прямым.

– длина действительной оси гиперболы,
– длина мнимой оси гиперболы,
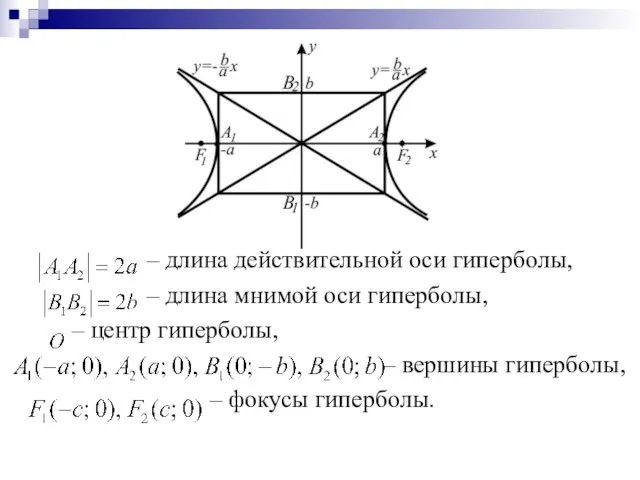
– центр гиперболы,
– вершины гиперболы,
– фокусы гиперболы.

Определение: Эксцентриситетом гиперболы называется отношение половины расстояния между фокусами к длине действительной полуоси гиперболы: (9).
Так как , то
Если , то гипербола называется равнобочной и ее асимптоты образуют прямой угол. Уравнение равнобочной гиперболы имеет вид:
(10)

Определение: Две гиперболы, у которых оси совпадают и равны, но действительная ось одной из них служит мнимой осью другой, и наоборот, называются сопряженными гиперболами.
Если уравнение одной из сопряженных гипербол
, то уравнение второй

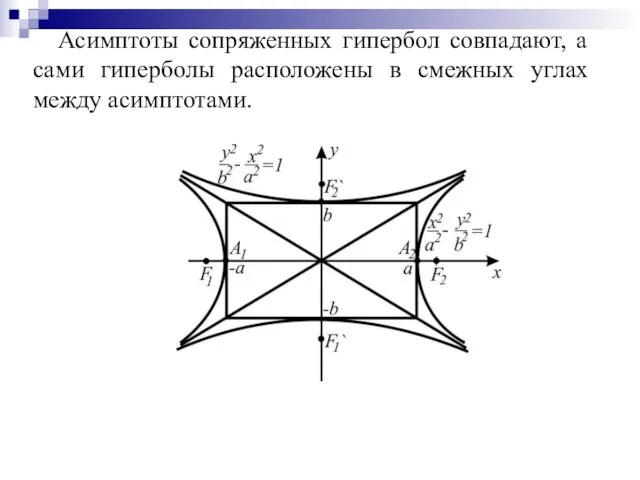
Асимптоты сопряженных гипербол совпадают, а сами гиперболы расположены в смежных углах между асимптотами.

Парабола
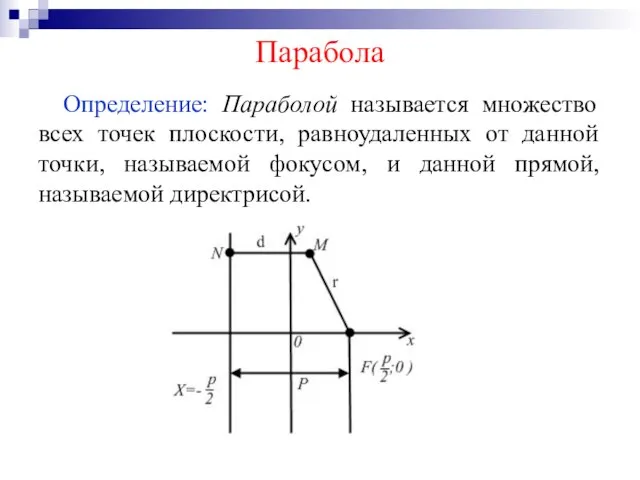
Определение: Параболой называется множество всех точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой.

Согласно определению точка М будет лежать на параболе, когда , где r – расстояние от точки до фокуса, d – расстояние от точки до директрисы.
Каноническое уравнение параболы имеет вид:
(11)
где р – параметр параболы (расстояние от фокуса до директрисы).
Параметр параболы характеризует ширину области ограниченной параболой. Чем больше р, тем шире распахнуты ветви параболы.

Парабола расположена симметрично относительно оси Ох , ветви направлены вправо.
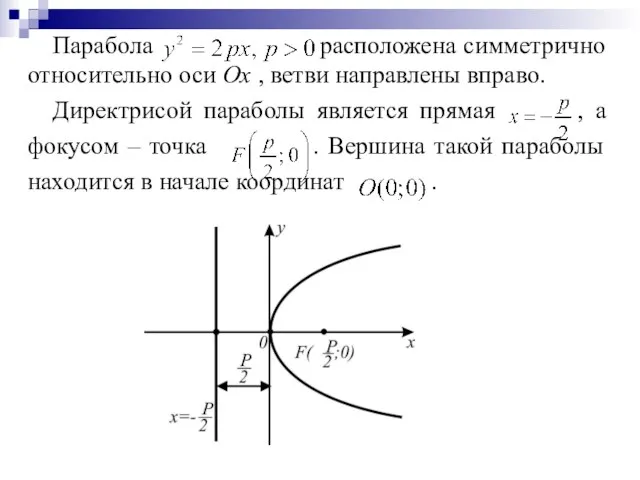
Директрисой параболы является прямая , а фокусом – точка . Вершина такой параболы находится в начале координат .

Парабола , расположена симметрично относительно оси Ох , ветви направлены влево.
Вершина параболы находится в точке . Директрисой параболы является прямая , а фокусом – точка .

Парабола , расположена симметрично относительно оси Оу , ветви направлены вверх.
Вершина параболы находится в точке . Директрисой параболы является прямая , а фокусом – точка .