Аналитические функции

Если существует предел отношения
при
по любому закону, то этот
предел называется производной функции f(z) в точке z:
Обозначают:

Требование существования предела отношения
и его независимость от закона стремления к нулю приращения переменной, накладывает на функцию более сильные ограничения, чем в случае функции действительного переменного.
Для функции действительного аргумента предел существует при приближении точки х+Δх к точке х по двум направлениям (слева и справа).
Для функции комплексного переменного точка z+Δz должна приближаться к точке z по любому пути, и пределы по всем направлениям должны быть одинаковы.

Пусть
тогда
где

Тогда
Если функция дифференцируема в точке z, то этот предел существует и не зависит от закона стремления
Если Δz = Δх, то есть точка z+Δz приближается к точке z по прямой, параллельной оси х, то

Если Δz = iΔy, то есть точка z+Δz приближается к точке z по прямой, параллельной оси у, то
Так как
не должен зависеть от закона стремления
то

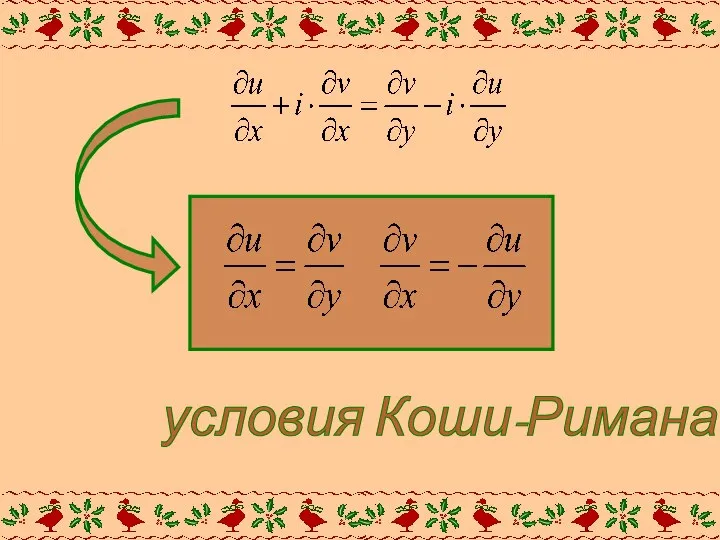
условия Коши-Римана

Это необходимое условие дифференцируемости ФКП. Оно должно выполнятся в любой точке, в которой функция f(z) дифференцируема.
Если функция комплексного аргумента
однозначна и дифференцируема не только
в данной точке, но и в некоторой
окрестности этой точки, то она
называется аналитической в данной точке.

Точки плоскости z, в которых функция f(z)
аналитична, называются правильными
точками этой функции.
Точки плоскости z, в которых функция f(z)
неаналитична, называются особыми
точками.
Функция, дифференцируемая во всех точках
некоторой области, называется
аналитической в данной области.

ПРИМЕРЫ.
1
Выяснить, являются ли данные
функции аналитичными:
2
3

1
Условия Коши-Римана выполняются во всех точках плоскости, следовательно функция является аналитичной на всей плоскости.

2
Условия Коши-Римана выполняются во всех точках плоскости, следовательно функция является аналитичной на всей плоскости.