Применение первообразной. Задания из открытого банка заданий ЕГЭ

Немного теории.
Первообразная, интеграл
и их применение

ПЕРВООБРАЗНАЯ
Функция F называется первообразной
для функции f, если выполняется условие

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Совокупность всех первообразных F(x)+c для функции f(x) называется неопределенным интегралом и обозначается
где f(x) – подинтегральная функция,
f(x)dx – подинтегральное выражение (дифференциал),
с – постоянная интегрирования.

Криволинейная трапеция
Отрезок [a;b] называют основанием
этой криволинейной трапеции
Криволинейной трапецией называется фигура,
ограниченная графиком непрерывной и не меняющей
на отрезке [а;b] знака функции f(х), прямыми
х=а, x=b и отрезком [а;b].

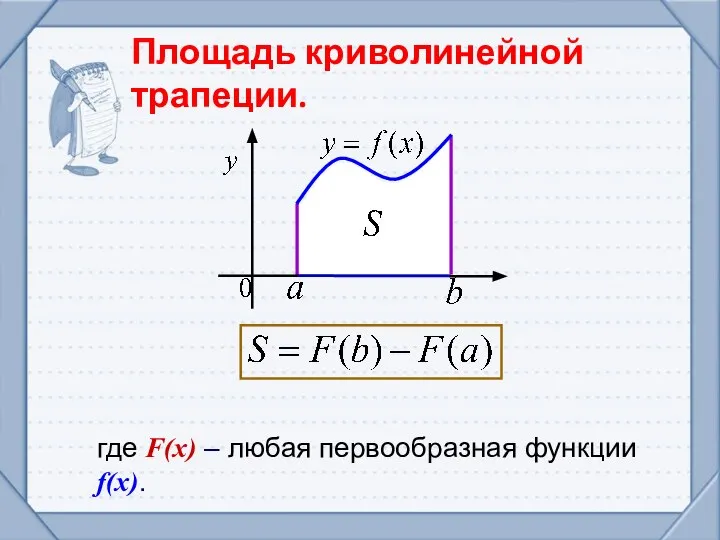
Площадь криволинейной трапеции.
где F(x) – любая первообразная функции f(x).

Формула Ньютона-Лейбница

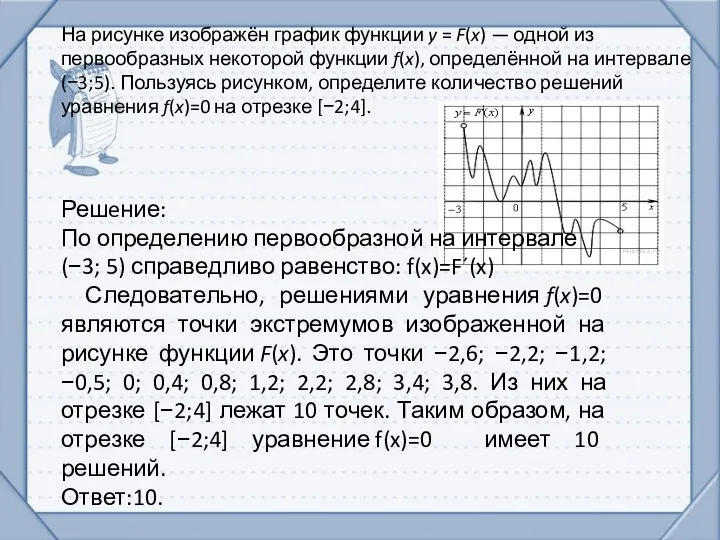
На рисунке изображён график функции y = F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (−3;5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [−2;4].
Решeние:
По определению первообразной на интервале
(−3; 5) справедливо равенство: f(x)=F´(x)
Следовательно, решениями уравнения f(x)=0 являются точки экстремумов изображенной на рисунке функции F(x). Это точки −2,6; −2,2; −1,2; −0,5; 0; 0,4; 0,8; 1,2; 2,2; 2,8; 3,4; 3,8. Из них на отрезке [−2;4] лежат 10 точек. Таким образом, на отрезке [−2;4] уравнение f(x)=0 имеет 10 решений.
Ответ:10.

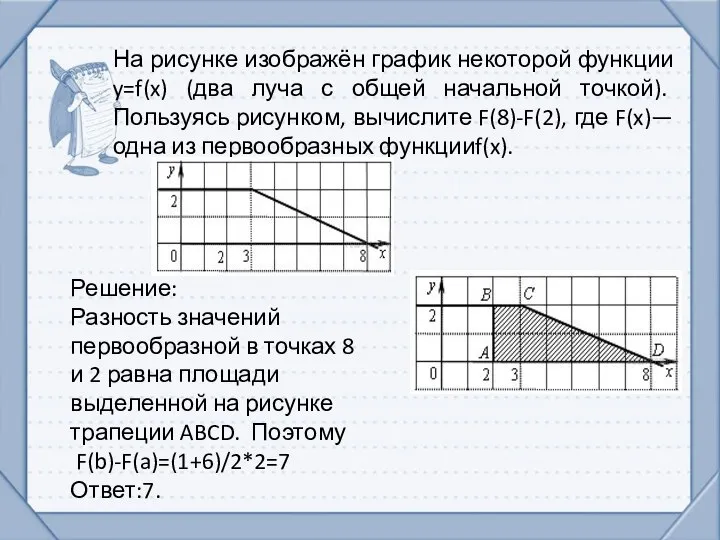
На рисунке изображён график некоторой функции y=f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8)-F(2), где F(x)—одна из первообразных функцииf(x).
Решение:
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции ABCD. Поэтому
F(b)-F(a)=(1+6)/2*2=7
Ответ:7.

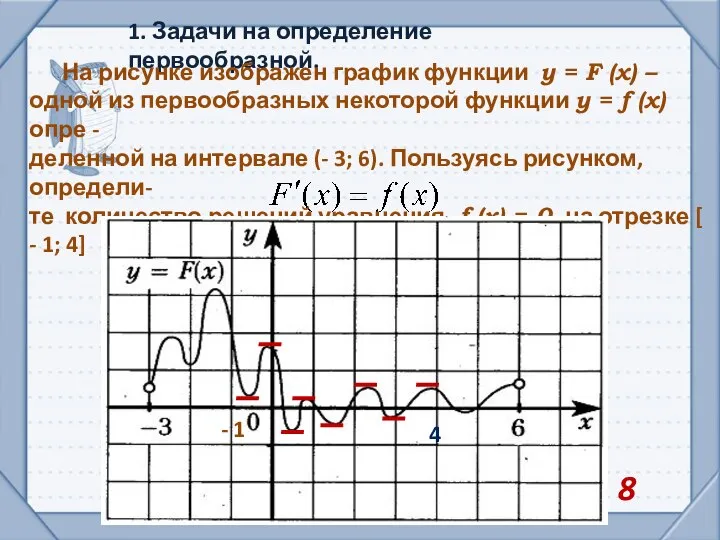
1. Задачи на определение первообразной.
На рисунке изображен график функции y = F (x) –
одной из первообразных некоторой функции y = f (x) опре -
деленной на интервале (- 3; 6). Пользуясь рисунком, определи-
те количество решений уравнения f (x) = 0 на отрезке [ - 1; 4]
- 1
4
8

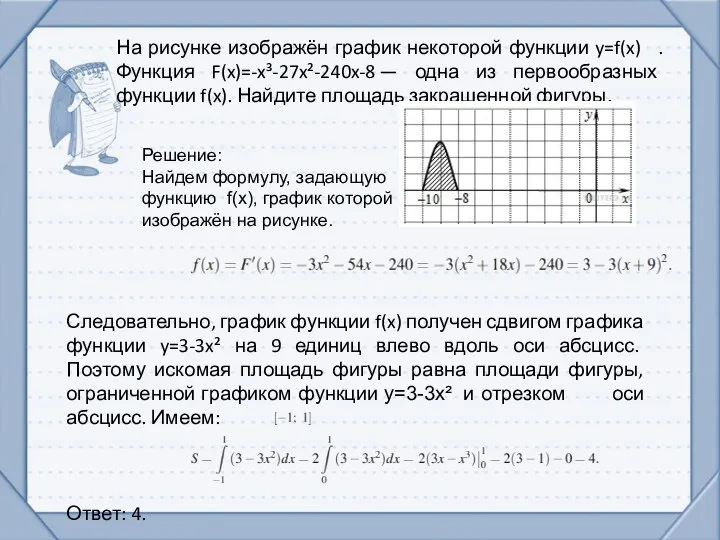
На рисунке изображён график некоторой функции y=f(x) . Функция F(x)=-x³-27x²-240x-8 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Решeние:
Найдем формулу, задающую функцию f(x), график которой изображён на рисунке.
Следовательно, график функции f(x) получен сдвигом графика функции y=3-3x² на 9 единиц влево вдоль оси абсцисс. Поэтому искомая площадь фигуры равна площади фигуры, ограниченной графиком функции y=3-3x² и отрезком оси абсцисс. Имеем:
Ответ: 4.