Справочник по геометрии

Не секрет, что порою для решения задачи не хватает знания какой-то одной-единственной формулы, которую хочется быстрее найти и применить, но не всегда эта формула находится под рукой, поэтому в презентации собраны самые важные и нужные формулы геометрии, которые могут пригодиться при решении различных заданий.
Важную роль играет использование математического справочника при самоподготовке к ЕГЭ в 11 классе и ГИА в 9 классе.
Создание справочника не закончено. Собраны основные формулы по курсу геометрии 7-9 классов. Работа над созданием справочника продолжается
Номинация: интерактивная презентация к урокам

Цели и задачи создания справочника:
систематизировать материал по основным математическим понятиям и формулам школьного курса геометрии;
создать учащимся условия для беспроблемного решения многих математических задач при выполнении домашнего задания, при подготовке к контрольным и самостоятельным работам, к ЕГЭ и ГИА;
способствовать развитию познавательной активности учащихся через знакомство с формулами, облегчающими процесс решения задачи;
способствовать развитию математических способностей одарённых детей через знакомство с формулами, не входящими в школьную программу по математике.

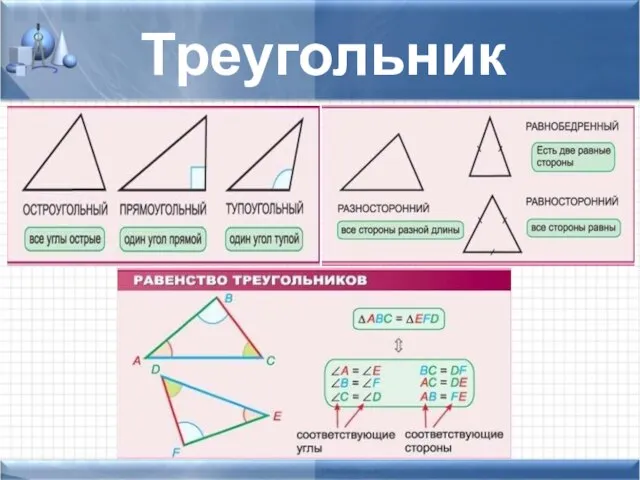
Треугольник

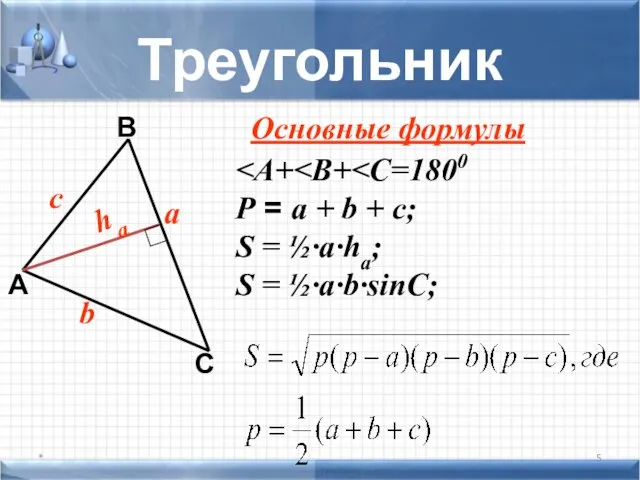
Треугольник
*
А
С
В
b
с
а
P = a + b + c;
S = ½·a·ha;
S = ½·a·b·sinC;
ha
Основные формулы

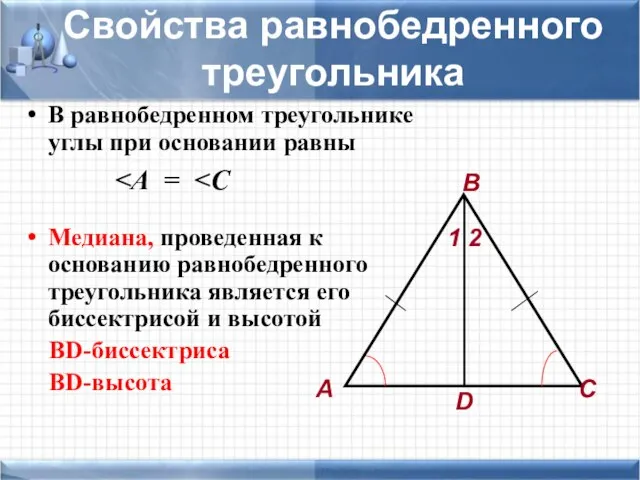
Свойства равнобедренного треугольника
В равнобедренном треугольнике углы при основании равны
Медиана, проведенная к основанию равнобедренного треугольника является его биссектрисой и высотой
ВD-биссектриса
ВD-высота
А
В
С
<А = <С
D
1
2

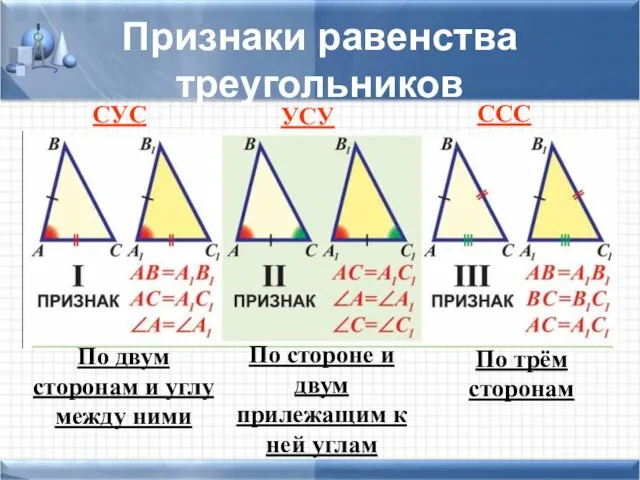
Признаки равенства треугольников
СУС
УСУ
ССС
По двум сторонам и углу между ними
По стороне и двум прилежащим к ней углам
По трём сторонам

Признаки равенства прямоугольных треугольников

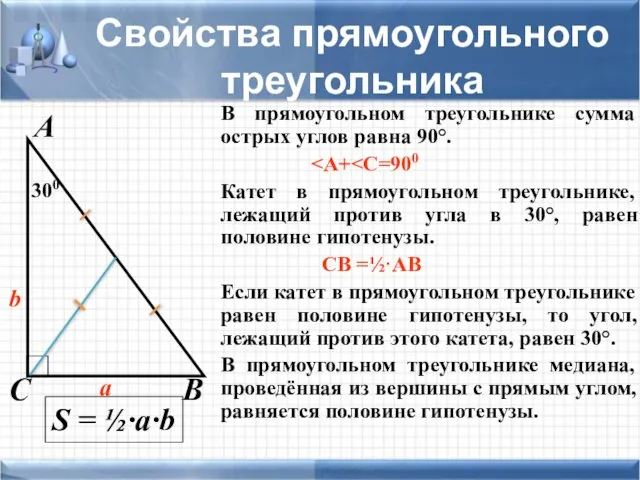
Свойства прямоугольного треугольника
В прямоугольном треугольнике сумма острых углов равна 90°.
Катет в прямоугольном треугольнике, лежащий против угла в 30°, равен половине гипотенузы.
CB =½·AB
Если катет в прямоугольном треугольнике равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
A
B
C
300
a
b
S = ½·a·b

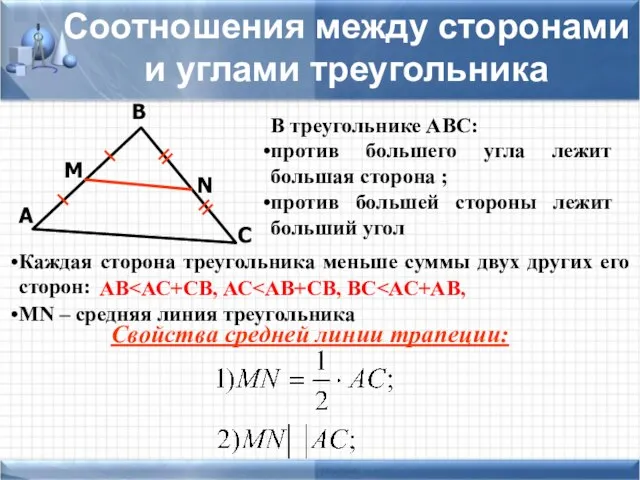
С
В
А
Соотношения между сторонами и углами треугольника
В треугольнике АВС:
против большего угла лежит большая сторона ;
против большей стороны лежит больший угол
АВ<АС+СВ, АС<АВ+СВ, ВС<АС+АВ,
Каждая сторона треугольника меньше суммы двух других его сторон:
M
N
MN – средняя линия треугольника
Свойства средней линии трапеции:

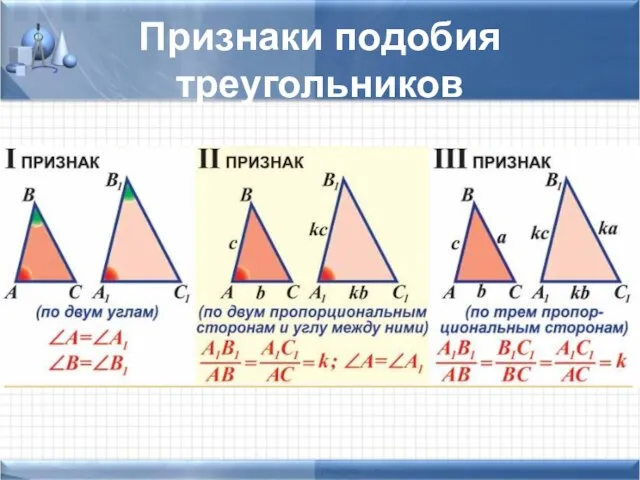
Признаки подобия треугольников

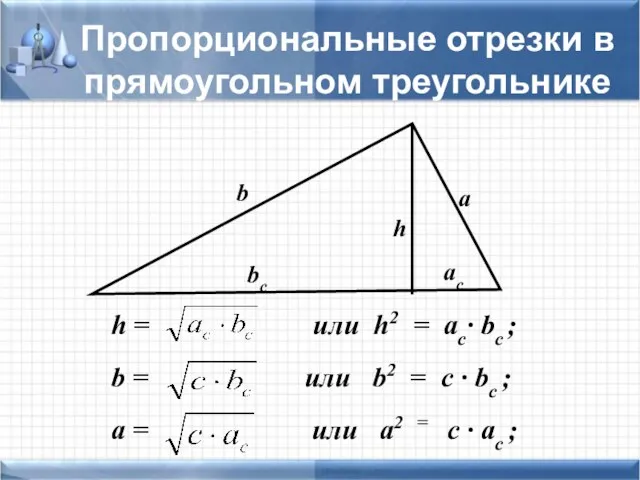
h = или h2 = ac· bc ;
b = или b2 = c · bc ;
a = или a2 = c · ac ;
b
a
h
bc
ac
Пропорциональные отрезки в прямоугольном треугольнике

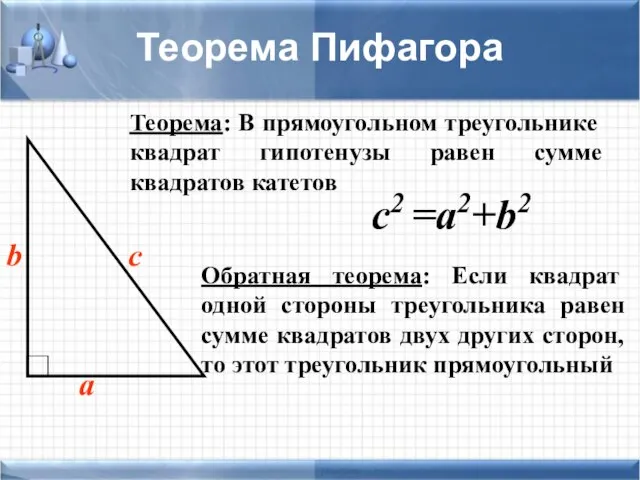
с2 =а2+b2
Теорема: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Теорема Пифагора
Обратная теорема: Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то этот треугольник прямоугольный

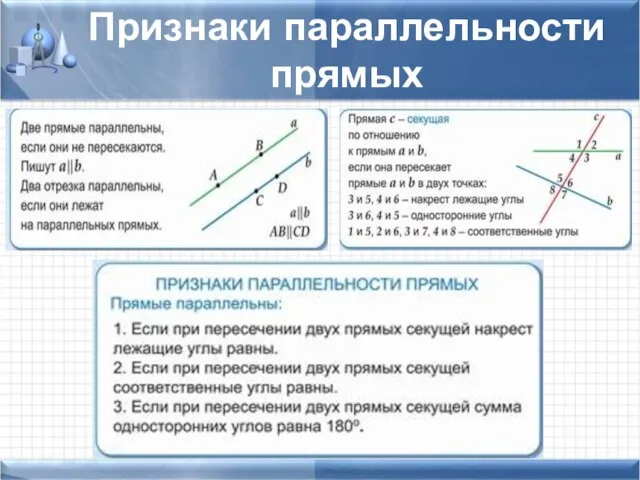
Признаки параллельности прямых

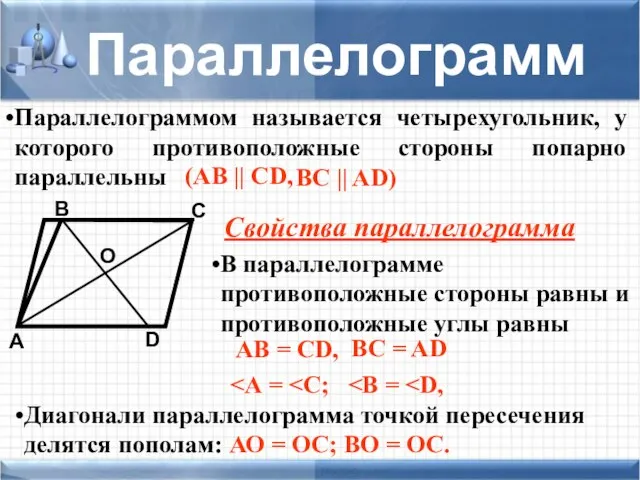
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны
D
А
В
С
(АB || CD,
BC || AD)
Параллелограмм
В параллелограмме противоположные стороны равны и противоположные углы равны
Диагонали параллелограмма точкой пересечения делятся пополам: АО = ОС; ВО = ОС.
АB = CD,
BC = AD
<А = <С;
О
Свойства параллелограмма

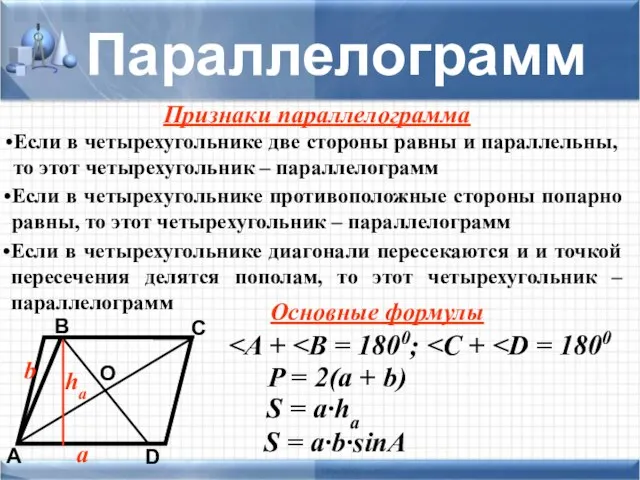
D
А
В
С
Параллелограмм
О
a
b
P = 2(a + b)
S = a·ha
ha
S = a·b·sinA
Признаки параллелограмма
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм
Если в четырехугольнике диагонали пересекаются и и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм
Основные формулы

Квадрат - это прямоугольник, у которого все стороны равны.
а
а
Квадрат
Квадрат обладает всеми свойствами и признаками параллелограмма, прямоугольника, ромба
Основные формулы
А
D
С
В
P = 4a
S = a2
S = ½·P·r
(r-радиус вписанной окружности)
(R-радиус описанной окружности)

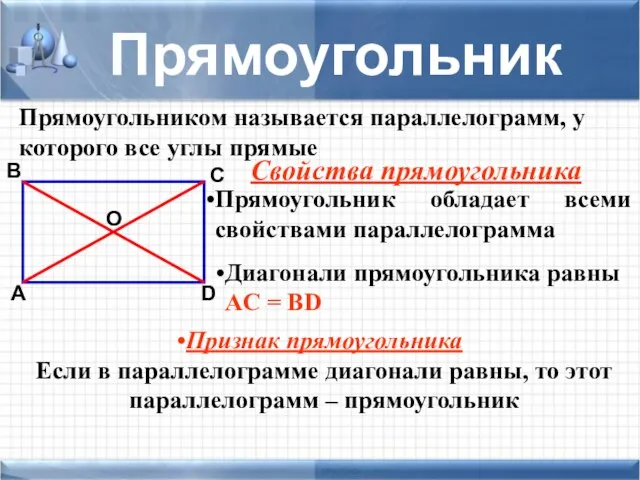
Прямоугольником называется параллелограмм, у которого все углы прямые
Прямоугольник
А
O
D
С
В
Диагонали прямоугольника равны AC = BD
Признак прямоугольника
Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник
Свойства прямоугольника
Прямоугольник обладает всеми свойствами параллелограмма

Прямоугольник
А
O
D
С
В
Основные формулы
a
b
P = 2(a + b)
S = a·b
Прямоугольником называется параллелограмм, у которого все углы прямые

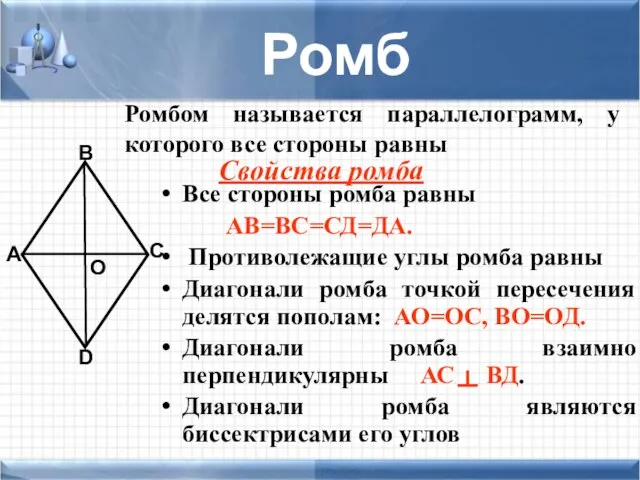
Все стороны ромба равны
АВ=ВС=СД=ДА.
Противолежащие углы ромба равны
Диагонали ромба точкой пересечения делятся пополам: АО=ОС, ВО=ОД.
Диагонали ромба взаимно перпендикулярны АС ВД.
Диагонали ромба являются биссектрисами его углов
А
В
С
D
О
Ромб
Ромбом называется параллелограмм, у которого все стороны равны
Свойства ромба

А
В
С
D
О
Ромб
Ромбом называется параллелограмм, у которого все стороны равны
Основные формулы
AВ = BС = CD = AD = a
P = 4a
a
d1
d2
S = ½·d1·d2
S = a·ha

Четырехугольник, у которого две стороны параллельны, а две другие нет, называется трапецией.
A
B
C
D
BC, AD–основания трапеции, ВС║АD
AB,CD – боковые стороны
Трапеция
M
N
MN –средняя линия трапеции
Свойства
средней линии трапеции:
P = АВ+ВС+СD+AD
Основные формулы
a
b
h
В равнобедренной трапеции углы при основаниях равны
В равнобедренной трапеции диагонали равны

Соотношения между сторонами и углами в прямоугольном треугольнике
а
b
с
А
В
С
Противолежащий катет
Прилежащий катет
Гипотенуза
-основное тригонометрическое тождество
Таблица значений sinα, cosα, tgα для некоторых углов

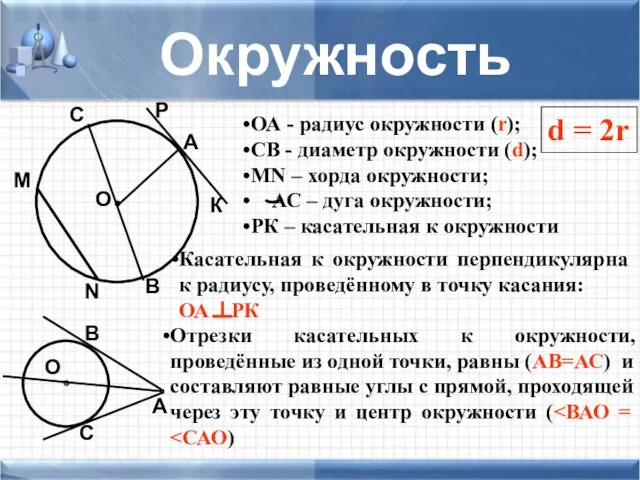
Окружность
О
А
ОА - радиус окружности (r);
СВ - диаметр окружности (d);
MN – хорда окружности; АС – дуга окружности;
РК – касательная к окружности
С
В
М
N
Р
К
Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания:
ОА РК
Отрезки касательных к окружности, проведённые из одной точки, равны (АВ=АС) и составляют равные углы с прямой, проходящей через эту точку и центр окружности (<ВАО = <САО)
d = 2r

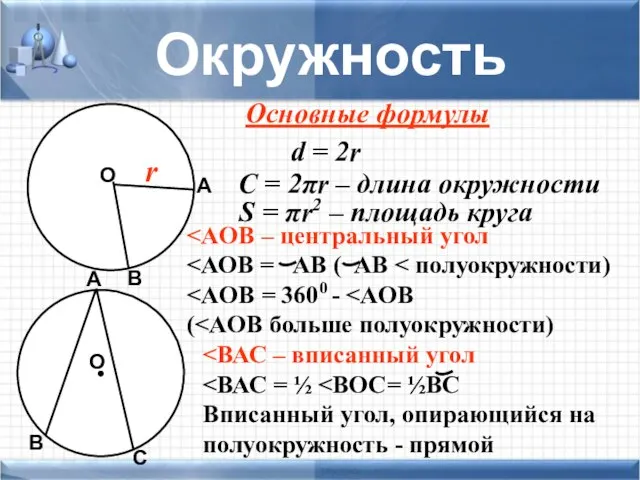
Окружность
Основные формулы
d = 2r
C = 2πr – длина окружности
S = πr2 – площадь круга
r
А
В
О
<АОВ = АВ ( АВ < полуокружности)
(
А
В
О
С
<ВАС – вписанный угол
<ВАС = ½
Вписанный угол, опирающийся на
полуокружность - прямой