Непрерывность функции

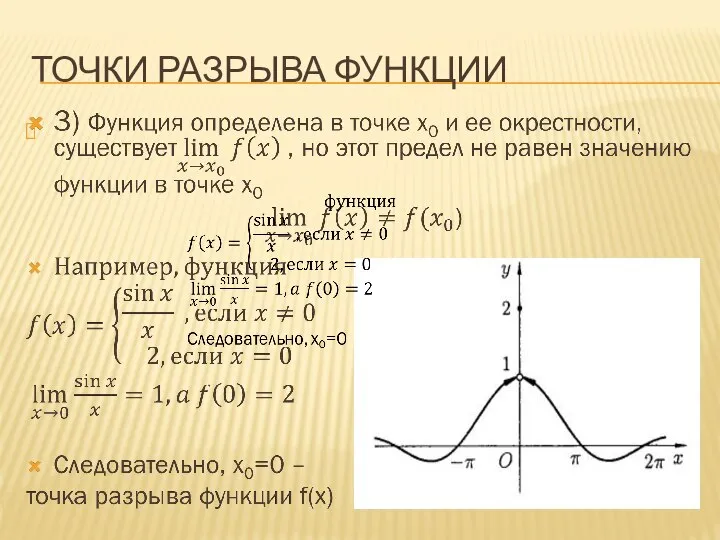
ОПРЕДЕЛЕНИЕ НЕПРЕРЫВНОЙ ФУНКЦИИ

НАХОЖДЕНИЕ ПРЕДЕЛА НЕПРЕРЫВНОЙ ФУНКЦИИ

ПРИМЕР 1

ОДНОСТОРОННЯЯ НЕПРЕРЫВНОСТЬ

ТОЧКИ РАЗРЫВА ФУНКЦИИ

ТОЧКИ РАЗРЫВА ФУНКЦИИ

ТОЧКИ РАЗРЫВА ФУНКЦИИ

ТОЧКИ РАЗРЫВА ФУНКЦИИ

КЛАССИФИКАЦИЯ РАЗРЫВОВ

КЛАССИФИКАЦИЯ РАЗРЫВОВ

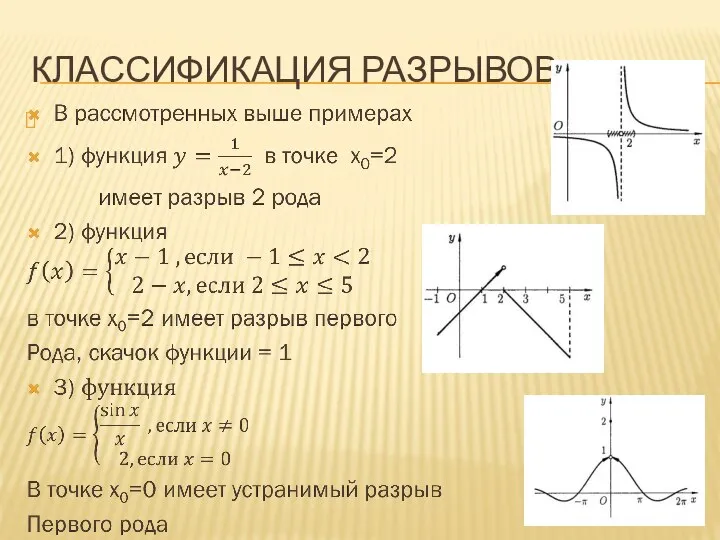
ТЕОРЕМЫ О НЕПРЕРЫВНОСТИ ФУНКЦИЙ
Т.1 Сумма , произведение и частное двух непрерывных функций есть функция непрерывная (для частного за исключением тех значений аргумента, в которых делитель равен нулю)
Т.2 Пусть функции y=f(x) непрерывна в точке хо, а функция z=g(y) непрерывна в точке y0 = f(xo). Тогда сложная функция g(f(x)), состоящая из
непрерывных функций, непрерывна в точке хо
Т.3 Если функция у = f(x) непрерывна и строго монотонна на [а;b] оси OX, то обратная функция также непрерывна и монотонна на соответствующем отрезке [c;d] оси Оу

ТЕОРЕМЫ О НЕПРЕРЫВНОСТИ ФУНКЦИЙ
Теорема Вейерштрасса. Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.
Теорема Больцано-Коши. Если функция у = f{x) непрерывна на отрезке [а;Ь] и принимает на его концах неравные значения f(a)=A , f(b)=B
то на этом отрезке она принимает и все промежуточные значения между А и В
Следствие. Если функция y=f(x) непрерывна на отрезке [а;Ь] и на его концах принимает значения разных знаков, то внутри отрезка [а;Ь] найдется хотя бы одна точка с, в которой данная функция f{x) обращается в нуль: f(с) = 0.

ИСПОЛЬЗОВАНИЕ ТЕОРЕМЫ БОЛЬЦАНО-КОШИ
Геометрический смысл теоремы:
если график непрерывной функции
переходит с одной стороны оси Ох
на другую, то он пересекает ось Ох
Следствие лежит в основе так называемого «метода половин­ного деления», который используется для нахождения корня уравнения
f(x) = 0.