Анализ данных. Описательные статистики

Анализ данных.
Описательная статистика
Задача описательных статистик — первичная систематизация данных, полученных экспериментально или в ходе наблюдений и их наглядное представление. В бизнесе статистика используются повсеместно, от расчета зарплат сотрудникам до анализа популярности бренда на рынке.
Рассмотрим основные описательные статистики и их практическое применение.
Кафедра информационно-аналитических систем

Анализ данных.
Описательная статистика
Центральная тенденция
Кафедра информационно-аналитических систем
Измерение центральной тенденции (measure of central
tendency) состоит в выборе одного числа, которое наилучшим
образом описывает все значения признака из набора данных.
Такое число называют центром, типическим значением для
набора данных, мерой центральной тенденции.

Анализ данных.
Описательная статистика
Плюсы и минусы центральной тенденции
Кафедра информационно-аналитических систем
Плюсы:
Получение информацию о распределении признака в сжатой
форме.
Можно сравнивать между собой два набора данных (две
выборки).
Минус:
Выбор центра ведет к потере информации по сравнению
с распределением частот.

Центральная тенденция
Мода
Медиана
Среднее значение
Средневзвешенное значение
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических систем

Анализ данных.
Описательная статистика
Мода
Кафедра информационно-аналитических систем
Мода – наиболее часто встречающееся значение в выборке, наборе данных. Обозначается Мо.

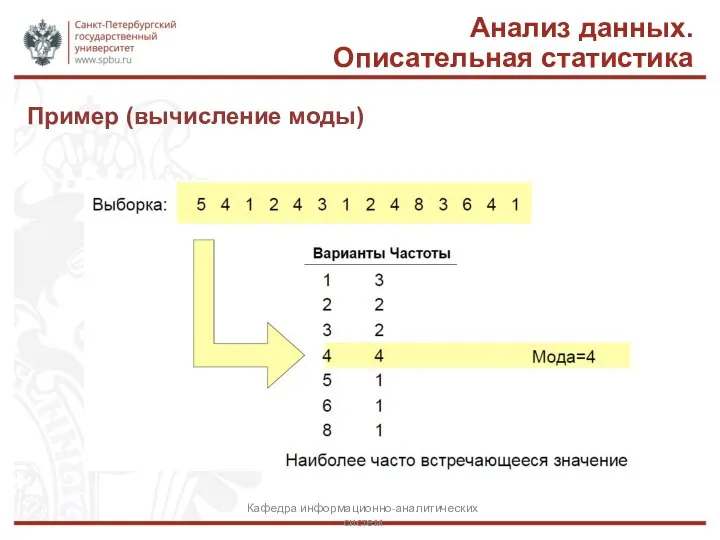
Пример (вычисление моды)
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических систем

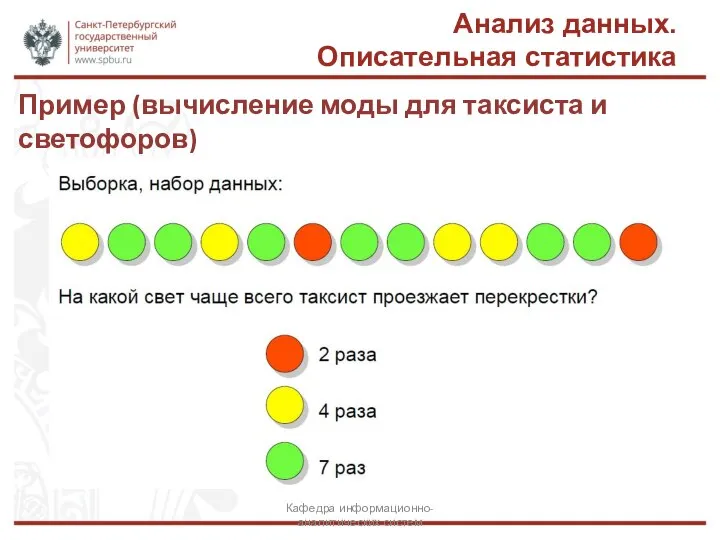
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических систем
Пример (вычисление моды для таксиста и светофоров)

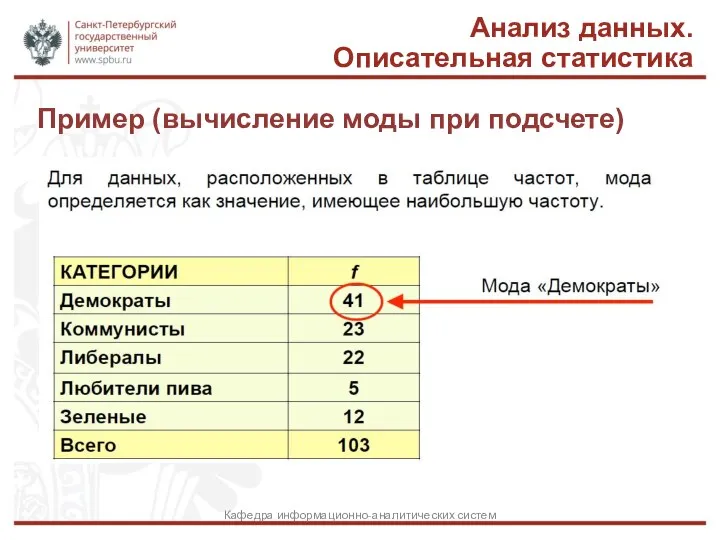
Пример (вычисление моды при подсчете)
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических систем

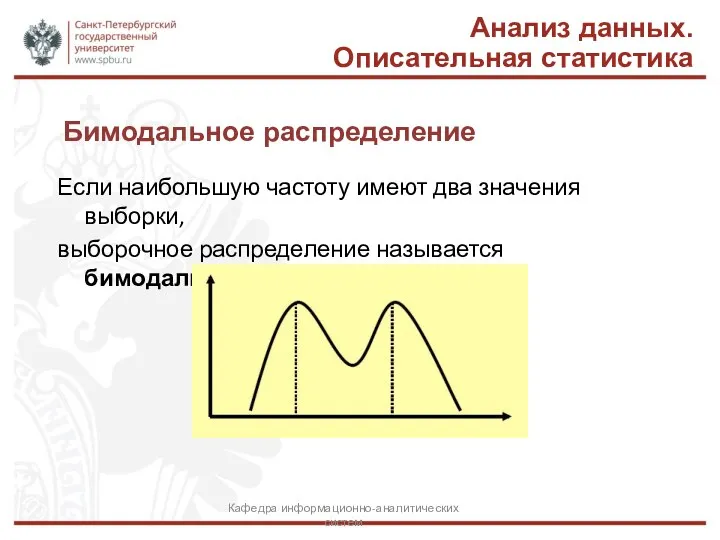
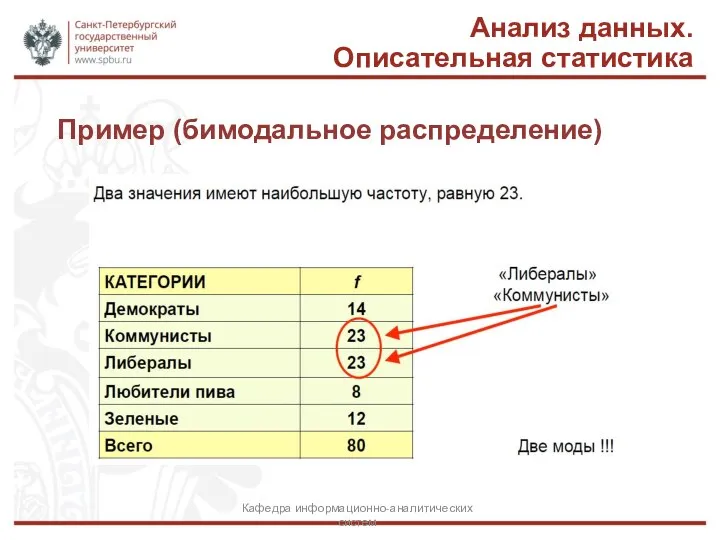
Бимодальное распределение
Если наибольшую частоту имеют два значения выборки,
выборочное распределение называется бимодальным.
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических систем

Пример (бимодальное распределение)
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических систем

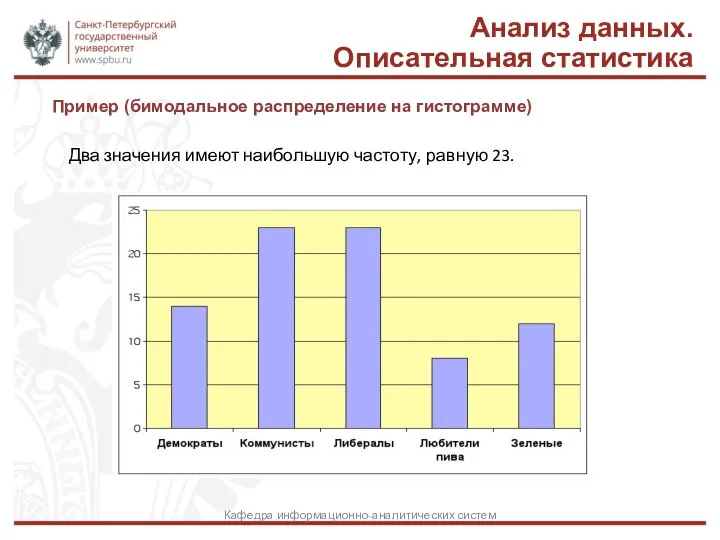
Пример (бимодальное распределение на гистограмме)
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических систем
Два значения имеют наибольшую частоту, равную 23.

А если моды вообще нет или больше двух?
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических систем
Если наибольшую частоту имеет более двух значений выборки, выборочное распределение называется мультимодальным. Если ни одно из значений не повторяется, мода отсутствует.

Свойства моды
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических систем
Наличие одного или двух крайних значений, сильно отличающихся от остальных, не влияет на значение моды.
Мода совпадает с точкой наибольшей плотности данных.
Мода может иметь несколько значений.
Мода может существовать для всех типов данных.
Мода - единственная мера центральной тенденции, которая работает в номинальной шкале!

Медиана
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических систем
Еще одна характеристика центральной тенденции - медиана. Медиана основывается на понятии вариационного ряда.

Анализ данных.
Описательная статистика
Вариационный ряд
Кафедра информационно-аналитических систем
Вариационный ряд – это упорядоченные данные, расположенные в порядке возрастания значения признака, либо в порядке убывания.
Назван так, поскольку содержит варианты значений признака.

Анализ данных.
Описательная статистика
Пример (вариационный ряд)
Кафедра информационно-аналитических систем
Набор данных:
6 1 3 7 1 7 3
После упорядочения (в порядке возрастания) получим вариационный ряд:
1 1 3 3 6 7 7
В порядке убывания получим другой вариационный ряд:
7 7 6 3 3 1 1

Медиана (Median)
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических систем
Медиана есть значение серединного элемента для вариационного ряда.
Обозначается Me.
Для нахождения медианы требуется набор данных превратить в вариационный ряд, то есть расположить все значения признака в порядке возрастания или убывания, а затем найти средний элемент. Он и есть медиана.

Вычисление медианы
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических систем
Для набора из n значений, если n нечетно, средний элемент имеет номер (N + 1)/ 2.
Если n четно, медиана находится как среднее арифметическое
двух соседних серединных элементов с номерами N/2 и N/2 +1.

Пример (вычисление медианы)
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических систем

Пример (вычисление медианы)
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических систем

Свойства медианы
Сильно отличающиеся от остальных данных крайние значения не влияют на величину медианы.
Значение медианы является единственным для каждого набора данных.
Медиана может быть определена не из полного набора данных. Достаточно иметь информацию об упорядоченности, общее число элементов в наборе и несколько значений, расположенных в середине вариационного ряда.
Медиана может быть определена для числовых и порядковых данных.
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических систем

Среднее (Mean)
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических систем
Выборочным средним будем называть среднее арифметическое выборки, то есть сумму всех значений выборки, деленную на ее объем выборки.

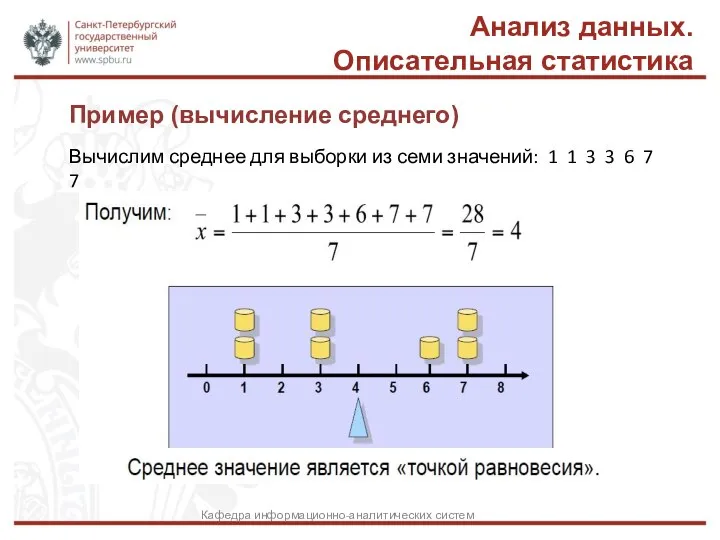
Пример (вычисление среднего)
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических систем
Вычислим среднее для выборки из семи значений: 1 1 3 3 6 7 7

Свойства среднего
Вычисляется только в числовых шкалах.
При вычислении необходимо использовать все данные.
Для каждого набора данных имеется только одно среднее.
Среднее есть единственная мера центральной тенденции, для которого сумма отклонений каждого значения от среднего равна нулю:
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических систем

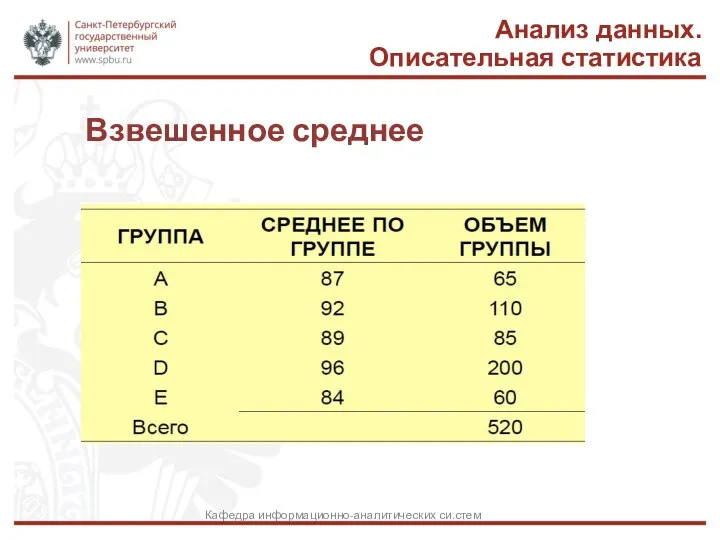
Взвешенное среднее
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических си.стем

Среднее взвешенное
Среднее взвешенное вычисляется по формуле:
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических си.стем

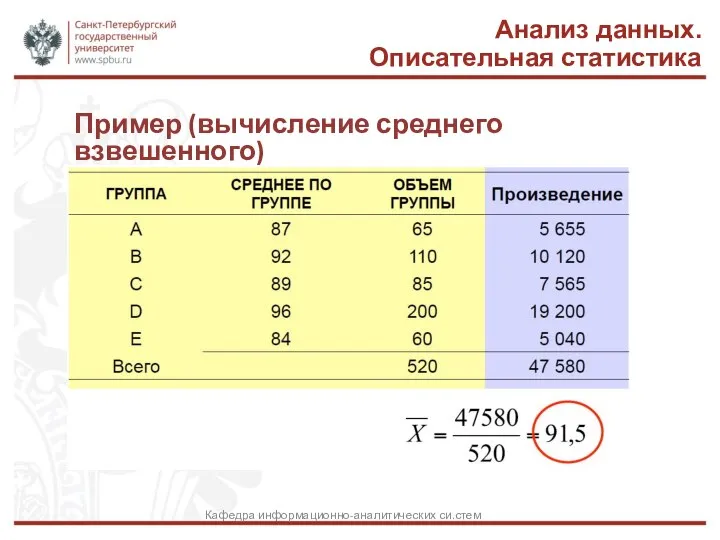
Пример (вычисление среднего взвешенного)
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических си.стем

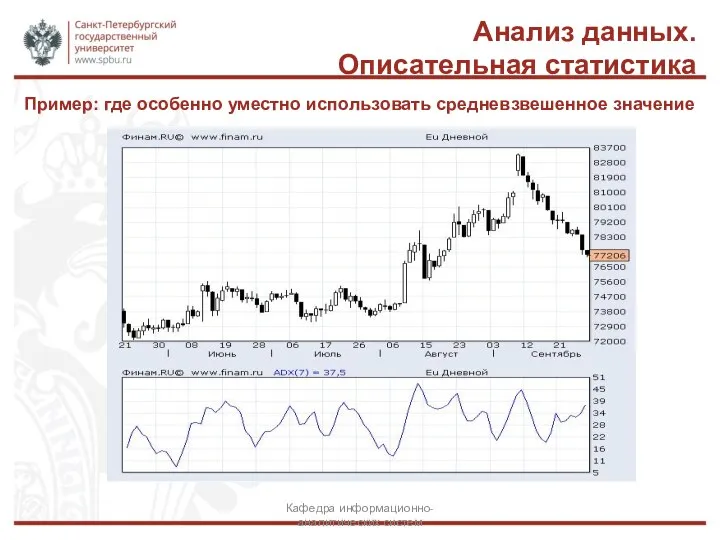
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических систем
Пример: где особенно уместно использовать средневзвешенное значение

Среднее для дихотомической шкалы
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических си.стем
Среднее может также применяться и для переменной, измеренной в дихотомической шкале. Если два значения признака кодируются 0 и 1, то среднее указывает долю (относительную частоту) единиц в выборке.
Пример: 1, 0, 0, 0, 1, 1, 1, 1, 1, 0
Среднее равно 0,6. То есть 60% значений выборки принимают значение, равное единице.

Среднее – не значит лучшее
Пример. В деревне 50 жителей. Среди них 49 человек –
крестьяне с месячным доходом в 1 тыс.рублей, а один житель – зажиточный владелец строительной фирмы, с месячным доходом 451 тыс.рублей. Среднее равно 10 тыс. рублей. Однако, вряд ли можно утверждать, что это число адекватно представляет доход жителей деревни. В этом случае, более разумно взять в качестве меры центральной тенденции моду или медиану (обе равны 1 тыс. рублей).
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических си.стем

Какое типическое значение наилучшее?
В зависимости от данных каждое из трех значений может стать наилучшим! Абсолютных рекомендаций нет.
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических си.стем

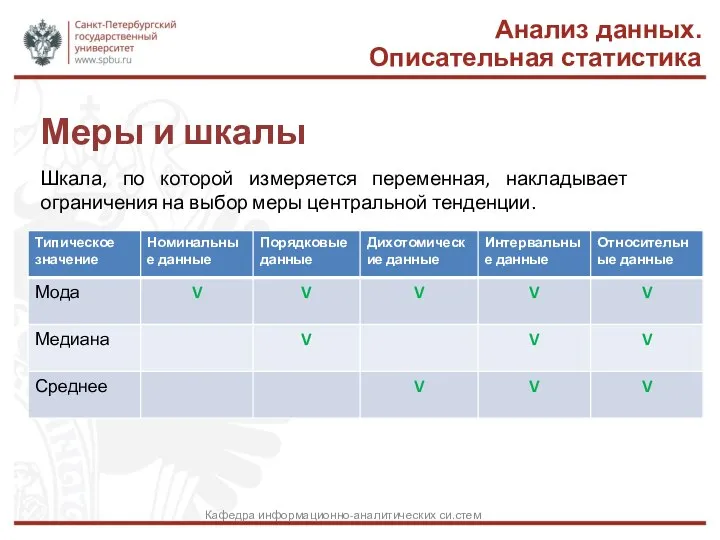
Меры и шкалы
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических си.стем
Шкала, по которой измеряется переменная, накладывает ограничения на выбор меры центральной тенденции.

Анализ данных.
Описательная статистика
Мера центральной тенденции – всего лишь одно число, которое не всегда достаточно емко может описать данные. Именно поэтому были придумано понятие размаха и квартильного размаха, как логическое продолжение мер центральной тенденции.
Кафедра информационно-аналитических систем

Пример (три выборки)
Рассмотрим три выборки:
999 1000 1001
900 1000 1100
1 1000 1999
Во всех трёх случаях среднее равно 1000. Однако это значение никаким образом не отражает особенности этих выборок.
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических си.стем

Размах (Range)
Размах – разность между наибольшим значением набора данных и наименьшим.
Анализ данных. Описательная статистика
Кафедра информационно-аналитических си.стем
Пример: Для набора данных 27, 3, 26, 19, 12, 10, 8, 6
размах равен R = 27 – 3 = 24.
Размах – уже неплохо, чтобы расширить наше представление о выборке но можно пойти и дальше.

Квартили (Quartile)
Под квартилями понимаются значения Q1,Q2,Q3 которые делят вариационный ряд на четыре равные части.
Второй квартиль Q2 совпадает с медианой.
Q1 - это медиана для значений, которые левее Q2.
Q3 - это медиана для значений, которые правее Q2.
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических си.стем

Анализ данных.
Описательная статистика
Проблемы с границами при определении квартилей
Есть разные способы определения Q1 и Q3. В некоторых сама медиана (Q2), полученная на предыдущем шаге учитывается при определении Q1, Q3, в других – нет (в литературе описывают по крайней мере 9 вариантов). Рассмотрим, как это делает EXCEL и ORACLE.
Кафедра информационно-аналитических систем

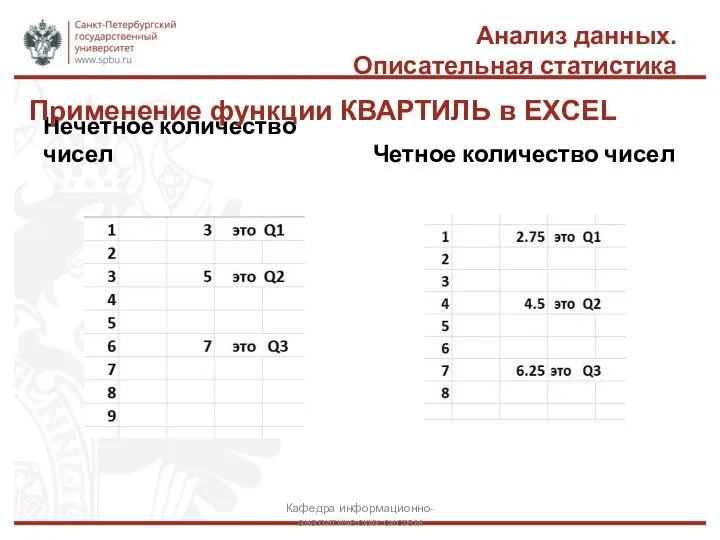
Анализ данных.
Описательная статистика
Нечетное количество чисел
Четное количество чисел
Кафедра информационно-аналитических систем
Применение функции КВАРТИЛЬ в EXCEL

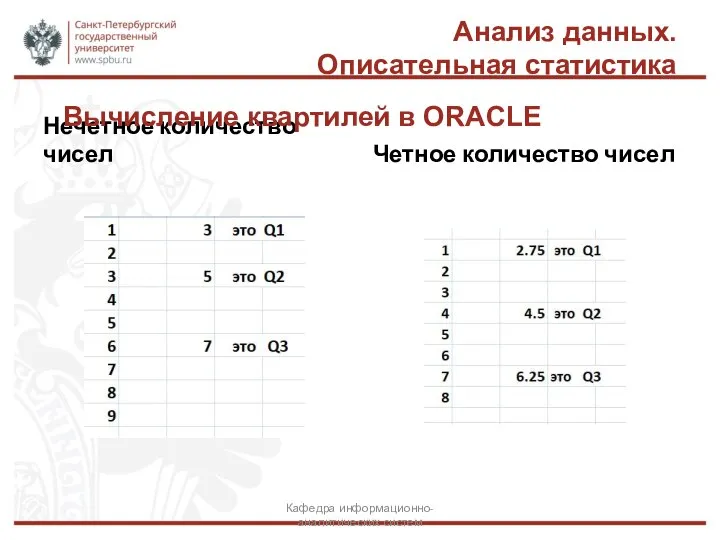
Анализ данных.
Описательная статистика
Нечетное количество чисел
Четное количество чисел
Кафедра информационно-аналитических систем
Вычисление квартилей в ORACLE

Размах квартилей (Inter Quartile Range)
Размах квартилей - это разница между третьим и первым квартилем и вычисляется по формуле:
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических си.стем

Сравнение размаха и квартильного размаха
При вычислении размаха используются только наибольшее и наименьшее значения признака. Распределение данных между ними полностью игнорируется.
Размах – очень простая мера вариации, но очень «грубая».
При вычислении квартильного размаха игнорируются только крайние значения, расположенные за пределами первого и третьего квартилей.
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических си.стем

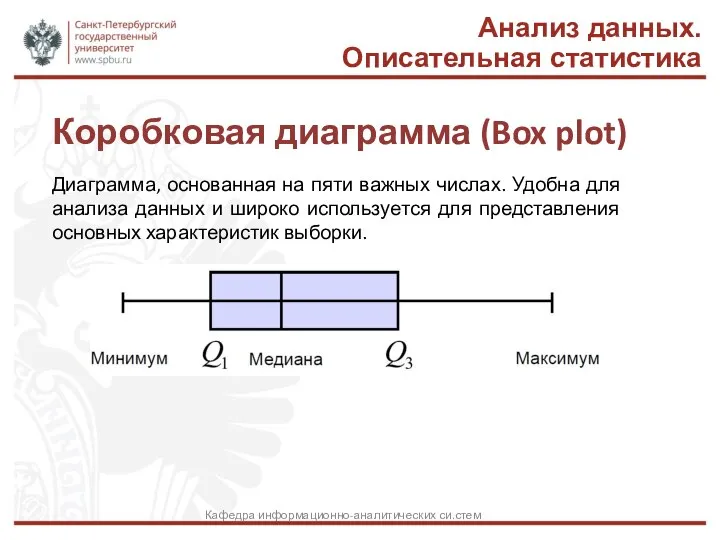
Коробковая диаграмма (Box plot)
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических си.стем
Диаграмма, основанная на пяти важных числах. Удобна для анализа данных и широко используется для представления основных характеристик выборки.

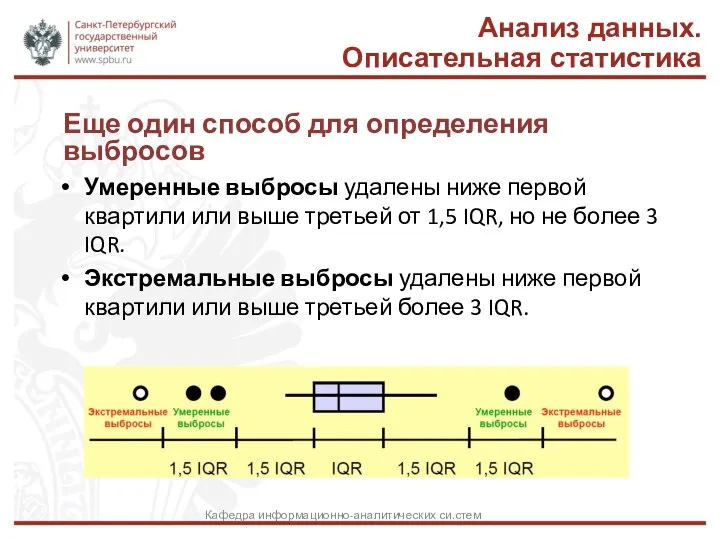
Еще один способ для определения выбросов
Умеренные выбросы удалены ниже первой квартили или выше третьей от 1,5 IQR, но не более 3 IQR.
Экстремальные выбросы удалены ниже первой квартили или выше третьей более 3 IQR.
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических си.стем

Пример (актеры и актрисы)
Имеются данные о возрасте актеров и актрис, в котором они были удостоены Оскара. Актеры:
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических си.стем
Актрисы:

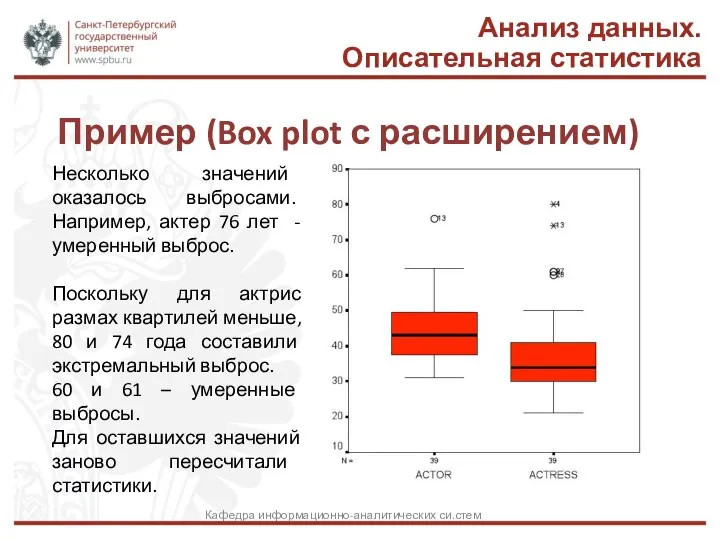
Пример (Box plot с расширением)
Анализ данных.
Описательная статистика
Кафедра информационно-аналитических си.стем
Несколько значений оказалось выбросами. Например, актер 76 лет - умеренный выброс.
Поскольку для актрис размах квартилей меньше, 80 и 74 года составили экстремальный выброс.
60 и 61 – умеренные выбросы.
Для оставшихся значений заново пересчитали статистики.

Анализ данных.
Описательная статистика
На сайте Москвы найдите открытые данные о том, как называли младенцев в 2015 – 2018 годах. На основании этих данных постройте три Box Plot диаграммы для своего имени и своих родителей (или братьев – сестер). Определите, были ли выбросы (умеренные или экстремальные за этот период).
Примечание: Срок сдачи: 2 недели с момента выдачи. Задание отправлять по адреcу: [e-mail].
Topic: DataMining_2018_job4
Кафедра информационно-аналитических систем
Задание 4