Содержание
- 2. Квадратный корень Определение. Квадратным корнем из числа а называют число t, квадрат которого равен а. t2
- 3. Корень n-й степени Определение. Корнем n-й степени из числа а называют число t, n-я степень которого
- 4. Арифметический корень n-й степени Определение. Неотрицательный корень n-й степени из числа а называется арифметическим корнем n-й
- 5. Обозначение корня Если n – нечетное число. Если а ≥0, то - арифметический корень n-й степени
- 6. Обозначение корня Если n – четное число. При четном n выражение имеет смысл только при а
- 7. Действие Чтобы отыскать корень n-ой степени - надо извлечь этот корень.
- 9. Скачать презентацию






 Презентация на тему Устный счёт 1 класс
Презентация на тему Устный счёт 1 класс  Фундаментальные и прикладные исследования в метрологии
Фундаментальные и прикладные исследования в метрологии Проценты. Определение, обозначение, вычисление, применение Математика 5 класс
Проценты. Определение, обозначение, вычисление, применение Математика 5 класс Логарифмическая спираль
Логарифмическая спираль Презентация на тему Угол. Прямой и развернутый угол
Презентация на тему Угол. Прямой и развернутый угол  Вычитание числа 7
Вычитание числа 7 Свойства числовых неравенств. 8 класс
Свойства числовых неравенств. 8 класс Презентация на тему Приведение дробей к общему знаменателю (6 класс)
Презентация на тему Приведение дробей к общему знаменателю (6 класс)  Обыкновенные дроби
Обыкновенные дроби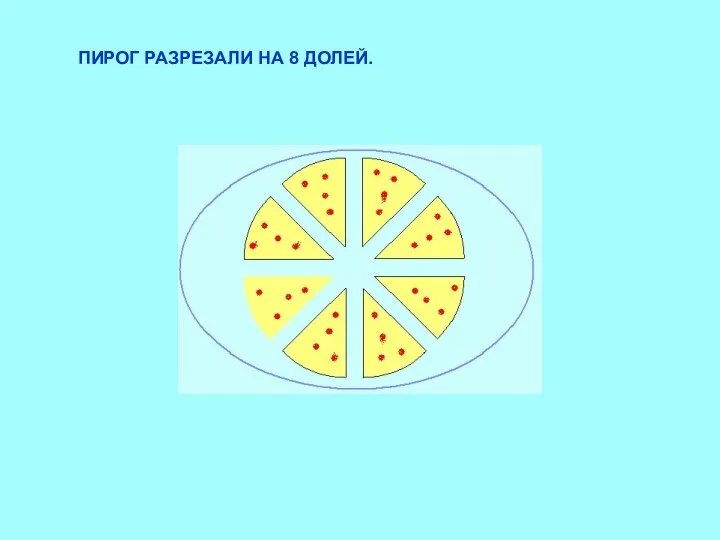 Обыкновенные дроби
Обыкновенные дроби parallelnost_1
parallelnost_1 Параллельность прямых и плоскостей в пространстве
Параллельность прямых и плоскостей в пространстве 2._3
2._3 Статистика. Статистика знает всё (Ильф и Петров). Выборочные исследования
Статистика. Статистика знает всё (Ильф и Петров). Выборочные исследования Теория о трех перпендикулярах
Теория о трех перпендикулярах Matematika_5_klass_21_09_Chtenie_i_zapis_naturalnykh_chisel (1)
Matematika_5_klass_21_09_Chtenie_i_zapis_naturalnykh_chisel (1) Элементы линейной алгебры и геометрии выпуклых множеств
Элементы линейной алгебры и геометрии выпуклых множеств Задачи на части
Задачи на части Вероятность события
Вероятность события Цифра в 21 веке
Цифра в 21 веке Решение неравенств
Решение неравенств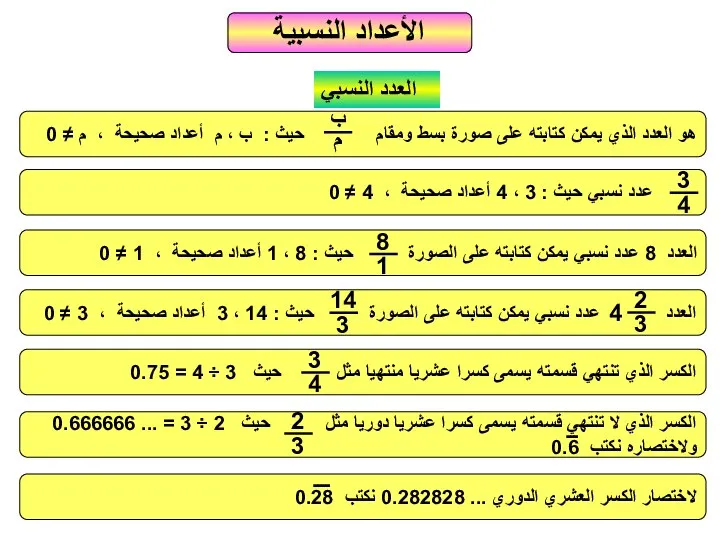 األعداد النسبية العدد النسبي ب
األعداد النسبية العدد النسبي ب Движение по окружности
Движение по окружности Математические структуры
Математические структуры Геометрическая интерпретация содержания задачи – условие успешного обучения каждого школьника решению математической задачи
Геометрическая интерпретация содержания задачи – условие успешного обучения каждого школьника решению математической задачи Игра
Игра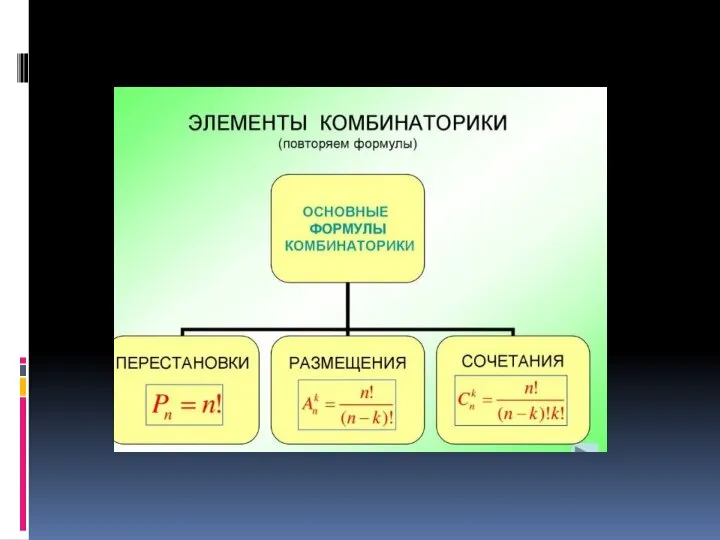 Основные понятия комбинаторики
Основные понятия комбинаторики Косинус угла
Косинус угла