Содержание
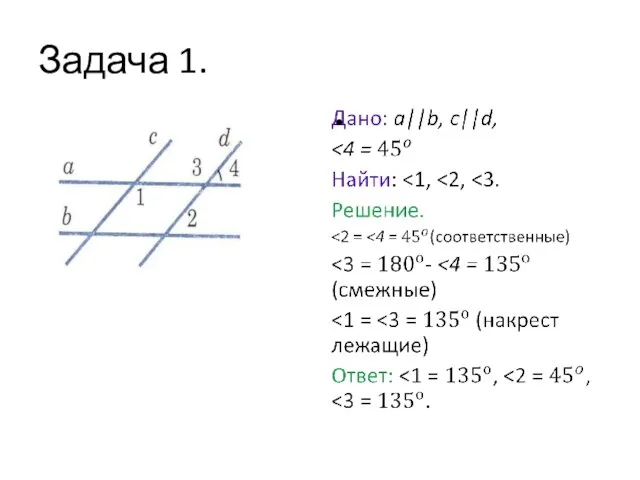
- 2. Задача 1.
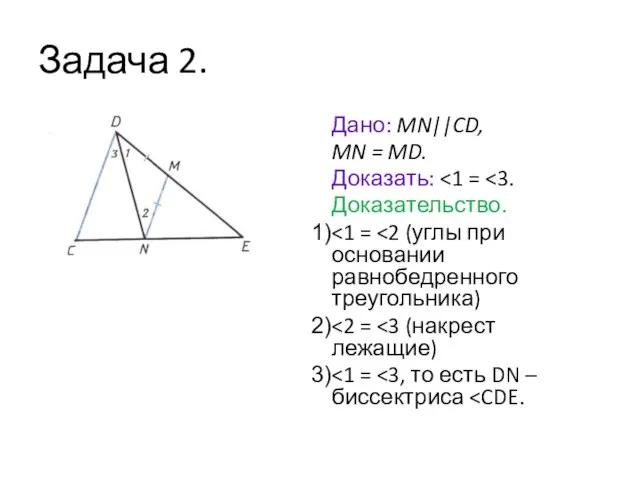
- 3. Задача 2. Дано: MN||CD, MN = MD. Доказать: Доказательство.
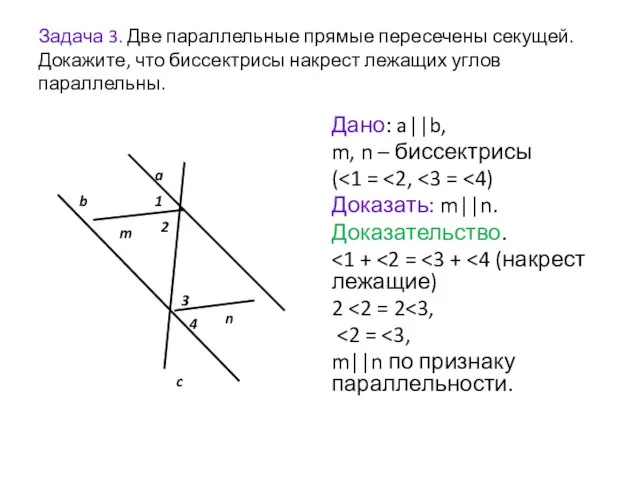
- 4. Задача 3. Две параллельные прямые пересечены секущей. Докажите, что биссектрисы накрест лежащих углов параллельны. Дано: a||b,
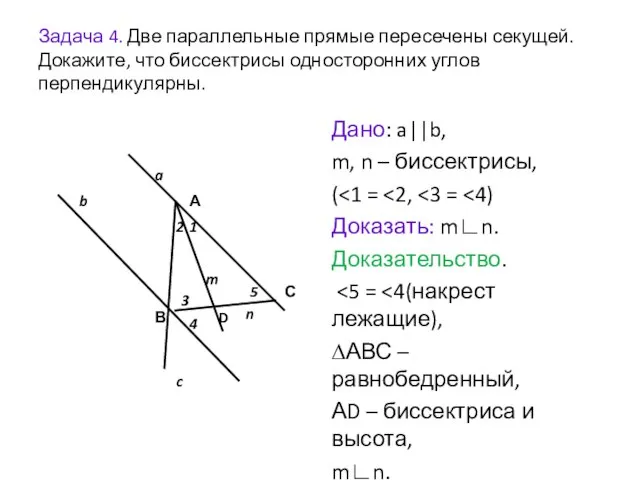
- 5. Задача 4. Две параллельные прямые пересечены секущей. Докажите, что биссектрисы односторонних углов перпендикулярны. Дано: a||b, m,
- 7. Скачать презентацию
 Деление дробей
Деление дробей Сложение вида +6
Сложение вида +6 Длина окружности
Длина окружности Линейные однородные дифференциальные уравнения с постоянными коэффициентами
Линейные однородные дифференциальные уравнения с постоянными коэффициентами Делим на равные части
Делим на равные части Тестовые задания
Тестовые задания Степень с натуральным показателем
Степень с натуральным показателем Определители второго и третьего порядка. 11 класс
Определители второго и третьего порядка. 11 класс Что такое проекция вектора
Что такое проекция вектора Проценты. Задачи на проценты
Проценты. Задачи на проценты Как построить график функции y=f(x)+m, если известен график функции y=f(x)
Как построить график функции y=f(x)+m, если известен график функции y=f(x) Функция
Функция Четные и нечётные функции
Четные и нечётные функции Область визначення функції
Область визначення функції Презентация на тему Дифференцирование частного и степени
Презентация на тему Дифференцирование частного и степени  Презентация на тему Грамм (3 класс)
Презентация на тему Грамм (3 класс)  Тренажёр Теремок. Математика - 1 класс
Тренажёр Теремок. Математика - 1 класс Умножение суммы на число
Умножение суммы на число Умножение величины на число
Умножение величины на число Сравнение числовых выражений
Сравнение числовых выражений Графический метод решения системы уравнений с двумя переменными
Графический метод решения системы уравнений с двумя переменными Умножение
Умножение Урок по теме Математика 6 класс Подготовлено Гаенко Т.А. Акимовская школа №3 Запорожской обл.
Урок по теме Математика 6 класс Подготовлено Гаенко Т.А. Акимовская школа №3 Запорожской обл. Презентация на тему Квадратный трёхчлен и его приложения
Презентация на тему Квадратный трёхчлен и его приложения  Решение задач, 1 класс
Решение задач, 1 класс Производная функции. Решения
Производная функции. Решения Математика. Решение задач
Математика. Решение задач Подготовка к ГИА. 9 класс
Подготовка к ГИА. 9 класс