Содержание
- 2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними. А В С
- 3. Следствие 1 Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними (
- 4. Следствие 2 Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними А С ABCD-
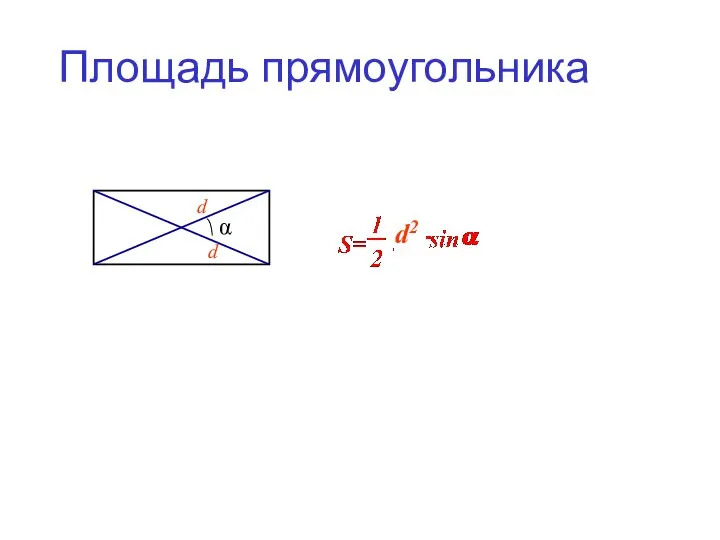
- 5. Площадь прямоугольника d α d d2
- 6. Площадь произвольного четырёхугольника A D B C α O d1 d2 ABCD- 4-угольник, BD=d1. AC=d2 ,
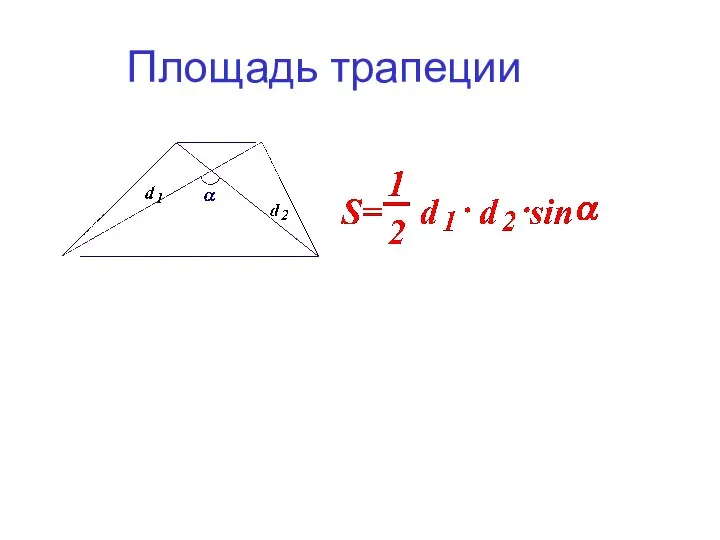
- 7. Площадь трапеции
- 8. Задания по готовым чертежам
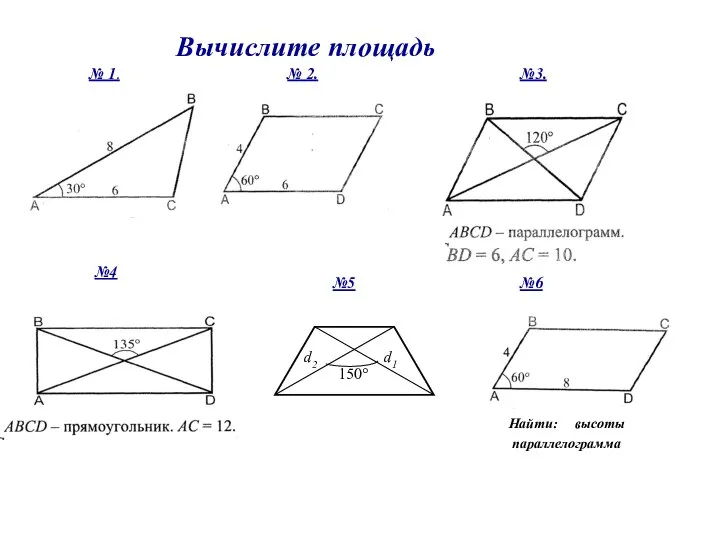
- 9. № 1. Вычислите площадь №3. №4 №5 d1 № 2. d2 150° d1 Найти: высоты параллелограмма
- 10. Теорема синусов
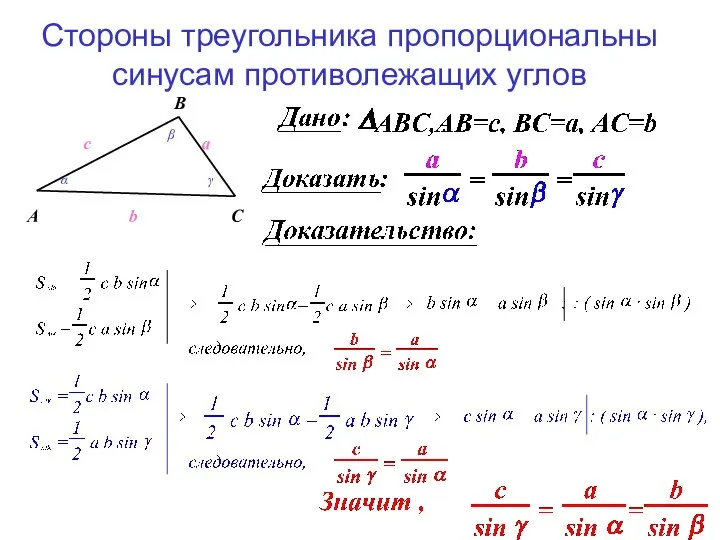
- 11. Стороны треугольника пропорциональны синусам противолежащих углов A B C a b c α β γ
- 12. Следствие 1 Отношение стороны треугольника к синусу противолежащего угла равно двум радиусам (диаметру) описанной окружности. ω
- 13. 2 случай ΔАВС- тупоугольный (докажите самостоятельно) . А В А1 С О а α 180°-α
- 14. Следствие 2 Площадь треугольника можно вычислить по формуле a, b, c – стороны треугольника, R –
- 15. Теорема косинусов
- 16. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус
- 17. Докажите самостоятельно , используя теорему косинусов , следующее утверждение: Сумма квадратов диагоналей параллелограмма равна сумме квадратов
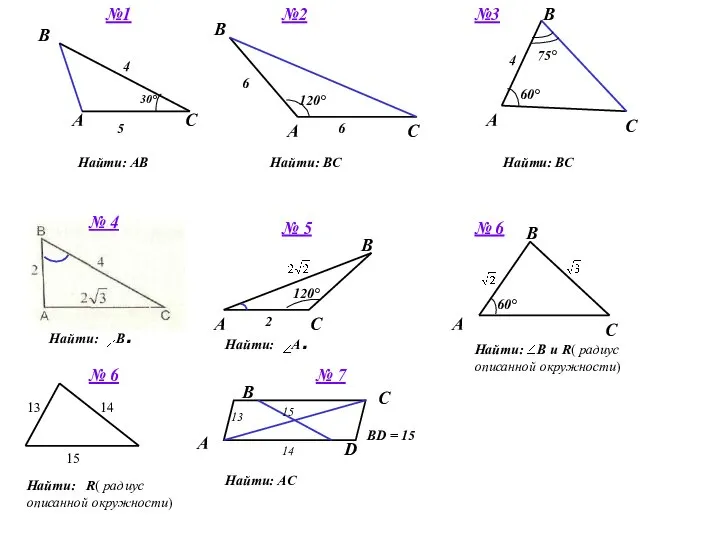
- 18. Задания по готовым чертежам
- 19. A B C 30° 5 Найти: АВ 4 №1 6 120° 6 С B А А
- 20. Задания по готовым чертежам
- 22. Скачать презентацию














 Задачи на движение в одном направлении из одной точки
Задачи на движение в одном направлении из одной точки Матрицы и действия над ними
Матрицы и действия над ними Разложение многочлена на множители
Разложение многочлена на множители Применение производной для исследования функции на монотонность и экстремумы
Применение производной для исследования функции на монотонность и экстремумы Тригонометрические уравнения и математические термины на английском языке
Тригонометрические уравнения и математические термины на английском языке Определители второго и третьего порядка
Определители второго и третьего порядка Решение систем уравнений с двумя переменными методом подстановки
Решение систем уравнений с двумя переменными методом подстановки Правильные многоугольники
Правильные многоугольники Основы анализа данных. Корреляционный анализ. (Лекция 5)
Основы анализа данных. Корреляционный анализ. (Лекция 5) Презентация на тему Число и цифра 7 (1 класс)
Презентация на тему Число и цифра 7 (1 класс)  Интерактивный тренажер. Числа от 1 до 1000. Нумерация (3 класс)
Интерактивный тренажер. Числа от 1 до 1000. Нумерация (3 класс) Презентация на тему Первый признак равенства треугольников
Презентация на тему Первый признак равенства треугольников  Время и работа. Связь между величинами
Время и работа. Связь между величинами Построение 3 видов группы геометрических тел
Построение 3 видов группы геометрических тел Решение простейших тригонометрических уравнений с помощью единичной окружности
Решение простейших тригонометрических уравнений с помощью единичной окружности Прямоугольный параллепипед. Итоговое повторение
Прямоугольный параллепипед. Итоговое повторение Признаки параллелограмма. 8 класс
Признаки параллелограмма. 8 класс Знакочередующиеся и знакопеременные ряды
Знакочередующиеся и знакопеременные ряды Величины. Объём
Величины. Объём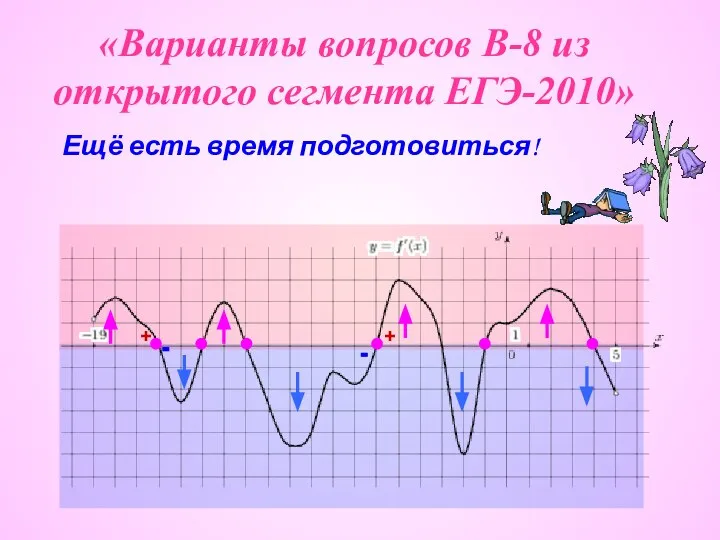 Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010
Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010 Задачи на кратное сравнение
Задачи на кратное сравнение Entrant
Entrant Решение задач (1 класс)
Решение задач (1 класс) Касательная плоскость к сфере
Касательная плоскость к сфере Наука Метрология
Наука Метрология Задача з піцою
Задача з піцою Тригонометрические уравнения
Тригонометрические уравнения Вычисление логарифмов
Вычисление логарифмов