attachment_642692504

Цель:
рассмотреть возможные случаи взаимного расположения прямых и плоскостей в пространстве
Задачи:
рассмотреть определения, лемму и теоремы по данной теме
самостоятельно доказать лемму и теорему

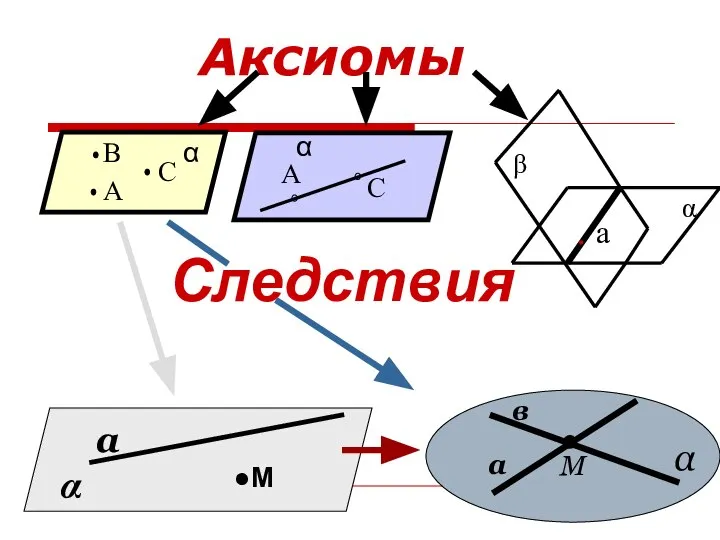
Аксиомы
Следствия

Каково может быть взаимное расположение двух прямых на плоскости?
Какие прямые в планиметрии называются параллельными?

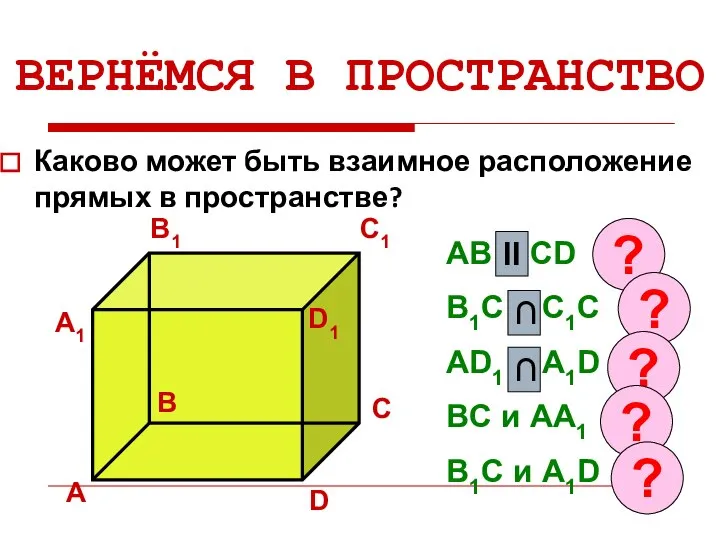
ВЕРНЁМСЯ В ПРОСТРАНСТВО
Каково может быть взаимное расположение прямых в пространстве?
А
B
C
D
А1
B1
C1
D1
AB и CD
B1C и C1C
AD1 и A1D
BC и AA1
B1C и A1D
II
?
∩
?
∩
?
?
?

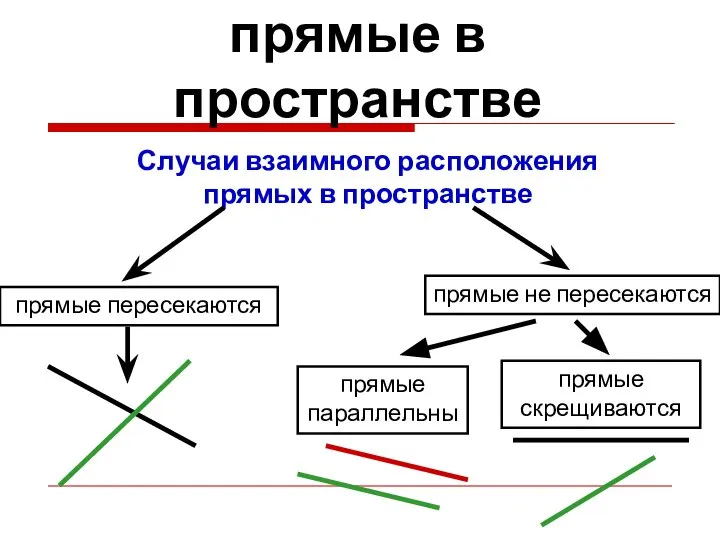
Случаи взаимного расположения прямых в пространстве
прямые параллельны
прямые пересекаются
прямые скрещиваются
Параллельные прямые в пространстве
прямые не пересекаются

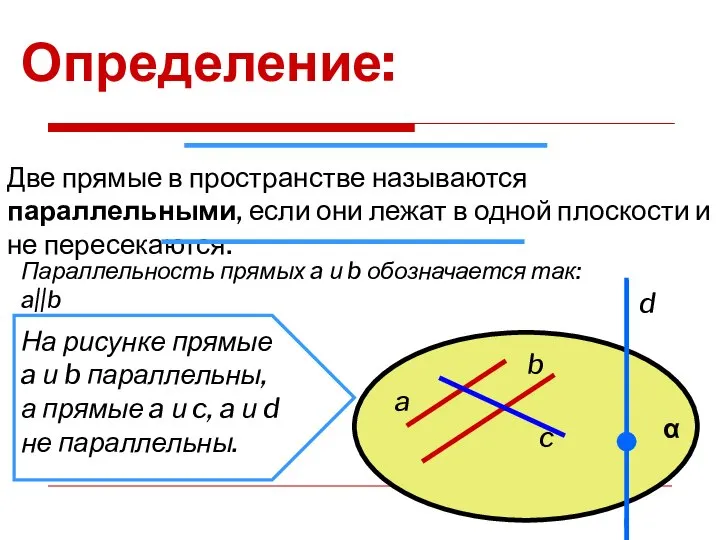
Определение:
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Параллельность прямых a и b обозначается так: a||b

Теорема:
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
Докажите теорему
?

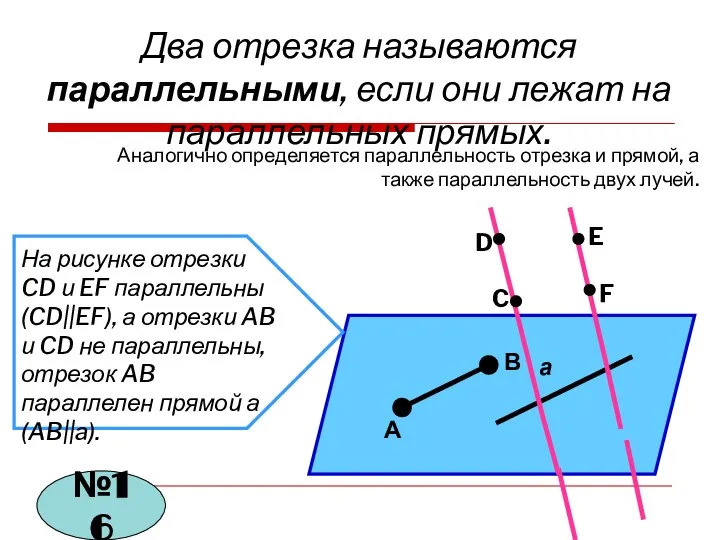
Два отрезка называются параллельными, если они лежат на параллельных прямых.
Аналогично определяется параллельность отрезка и прямой, а также параллельность двух лучей.
№16

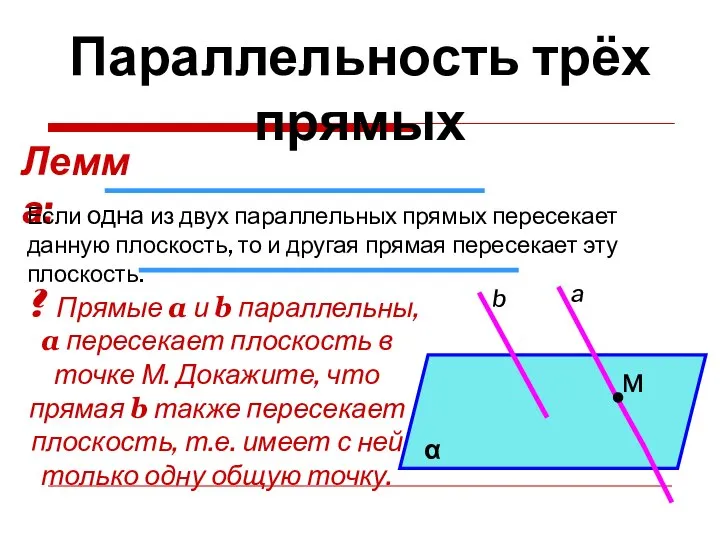
Параллельность трёх прямых
Лемма:
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Прямые a и b параллельны, а пересекает плоскость в точке М. Докажите, что прямая b также пересекает плоскость, т.е. имеет с ней только одну общую точку.
?

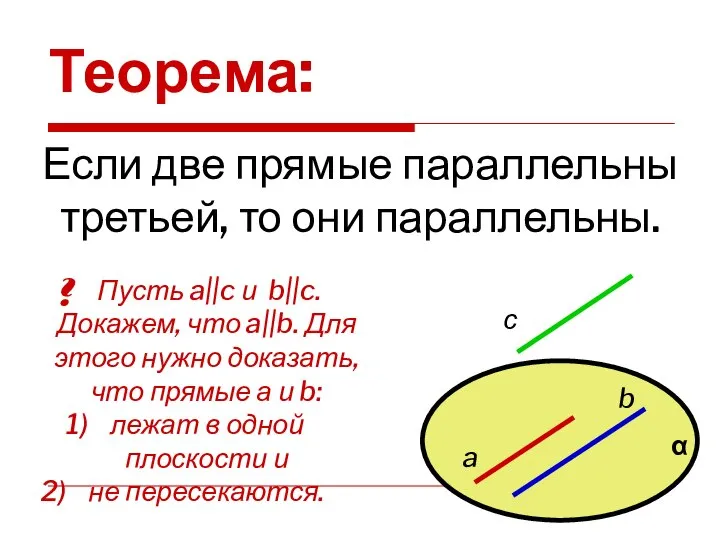
Теорема:
Если две прямые параллельны третьей, то они параллельны.
Пусть a||c и b||c. Докажем, что a||b. Для этого нужно доказать, что прямые а и b:
лежат в одной плоскости и
не пересекаются.
?

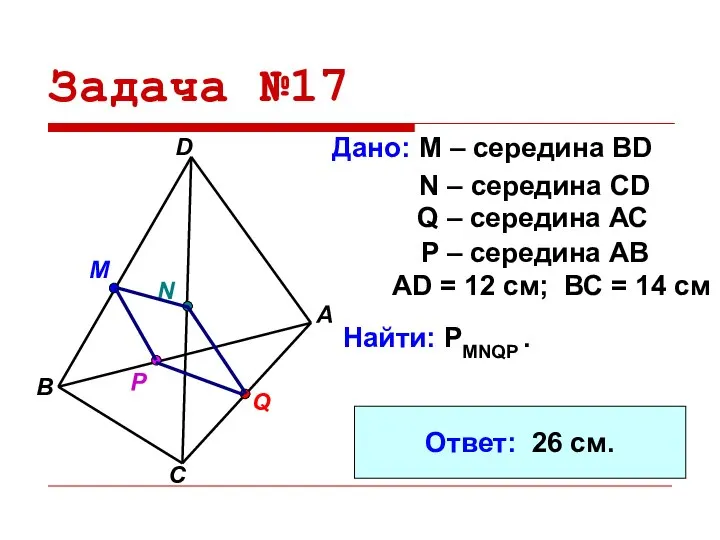
Задача №17
Дано: М – середина BD
A
B
D
C
N
M
Р
Q
N – середина CD
Q – середина АС
P – середина АВ
АD = 12 см; ВС = 14 см
Найти: PMNQP .
Ответ: 26 см.

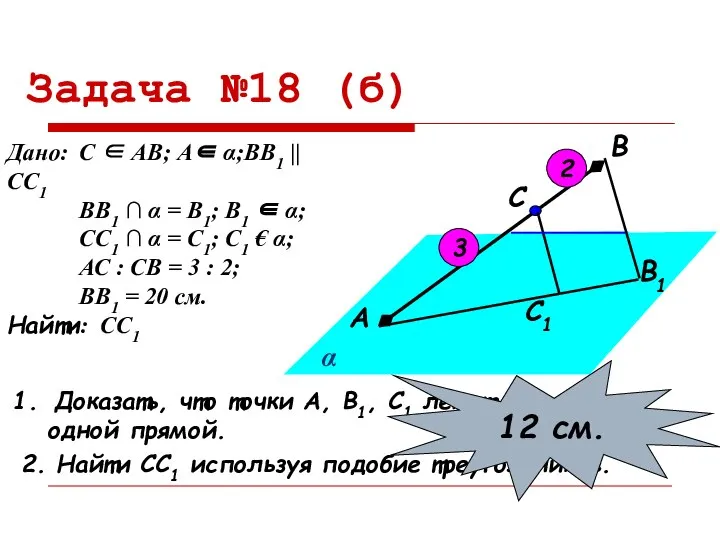
Задача №18 (б)
С1
В1
С
В
А
α
Доказать, что точки А, В1, С1 лежат на
одной прямой.
Дано: С ∈ АВ; А∈ α;ВВ1 || СС1
ВВ1 ∩ α = В1; В1 ∈ α;
СС1 ∩ α = С1; С1 € α;
АС : СВ = 3 : 2;
ВВ1 = 20 см.
Найти: СС1
2. Найти СС1 используя подобие треугольников.
12 см.
3
2

?
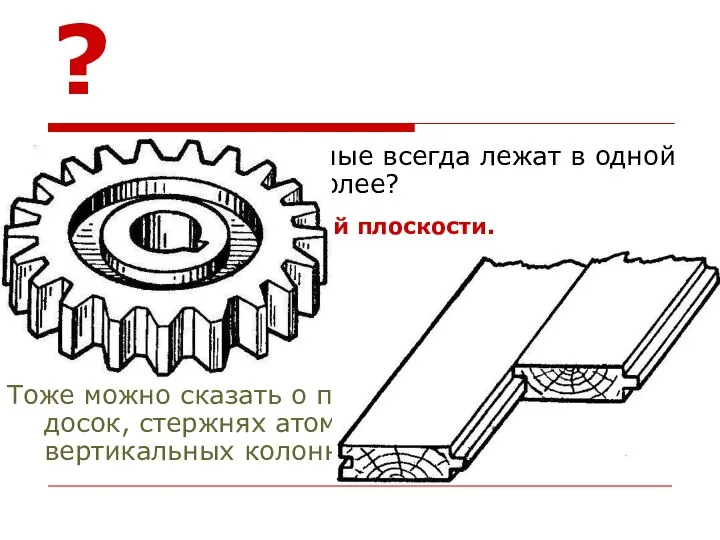
Две параллельные прямые всегда лежат в одной плоскости. А три и более?
Могут и не лежать в одной плоскости.
Например, все рёбра прямозубой цилиндрической шестерни лежат на параллельных прямых, но не принадлежат одной плоскости.
Тоже можно сказать о продольных шпунтовых досок, стержнях атомного реактора, вертикальных колоннах строящегося дома и т.д.

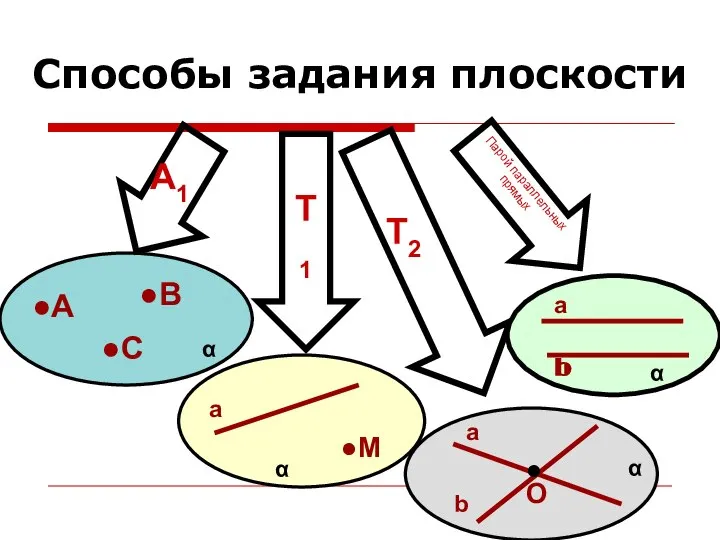
Способы задания плоскости
Т1

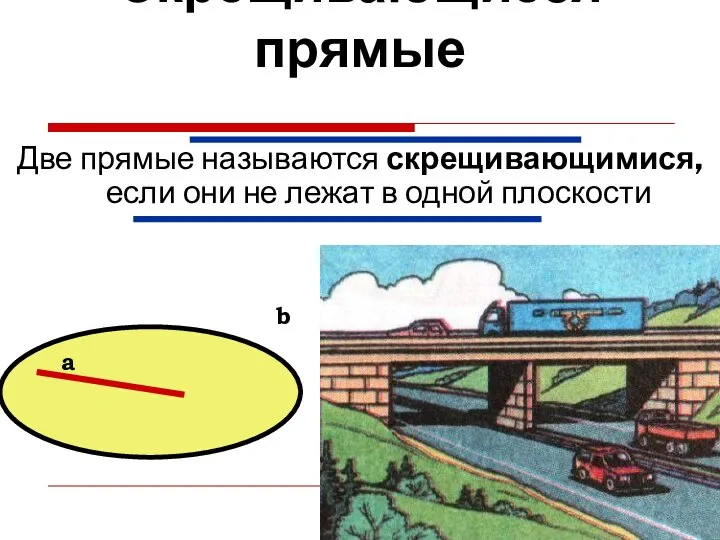
Скрещивающиеся прямые
Две прямые называются скрещивающимися, если они не лежат в одной плоскости
b

Теорема:
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Допустим, что прямые АВ и СD лежат в некоторой плоскости β.

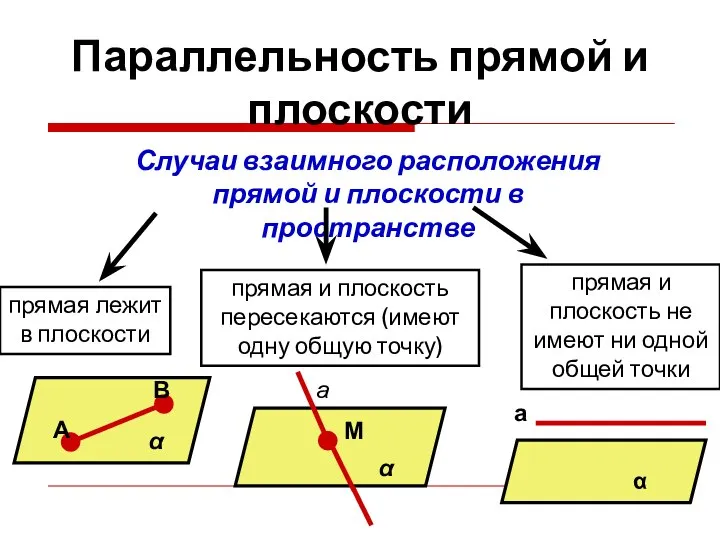
Параллельность прямой и плоскости
Случаи взаимного расположения прямой и плоскости в пространстве
прямая лежит в плоскости
прямая и плоскость пересекаются (имеют одну общую точку)
прямая и плоскость не имеют ни одной общей точки

Определение:
Прямая и плоскость называются параллельными, если они не имеют общих точек.
Теорема:
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
Докажите теорему методом от противного
?

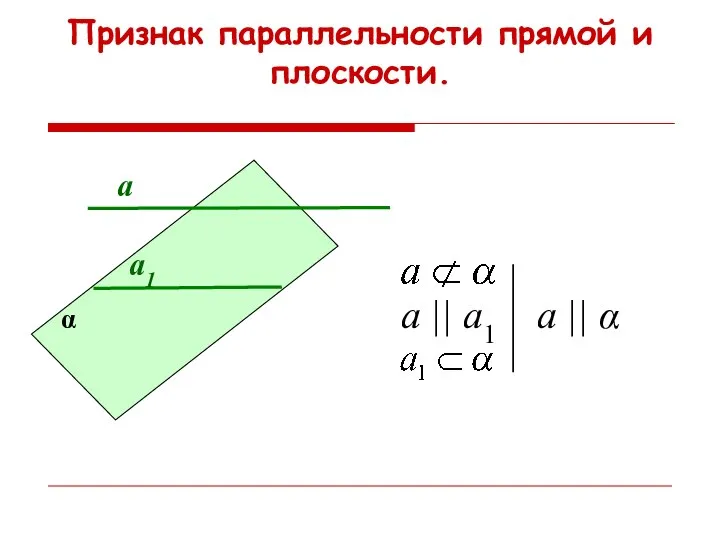
а1
а
α
а || а1
а || α
Признак параллельности прямой и плоскости.

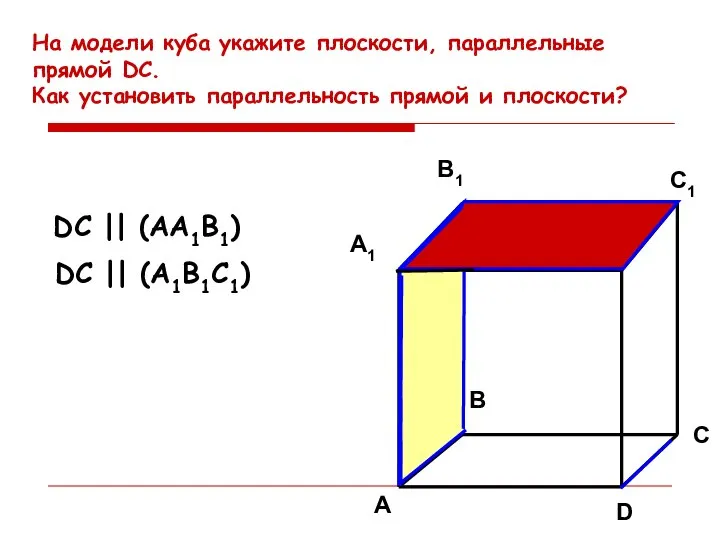
На модели куба укажите плоскости, параллельные прямой DC.
Как установить параллельность прямой и плоскости?
C1
C
DC || (AA1B1)
DC || (A1B1C1)

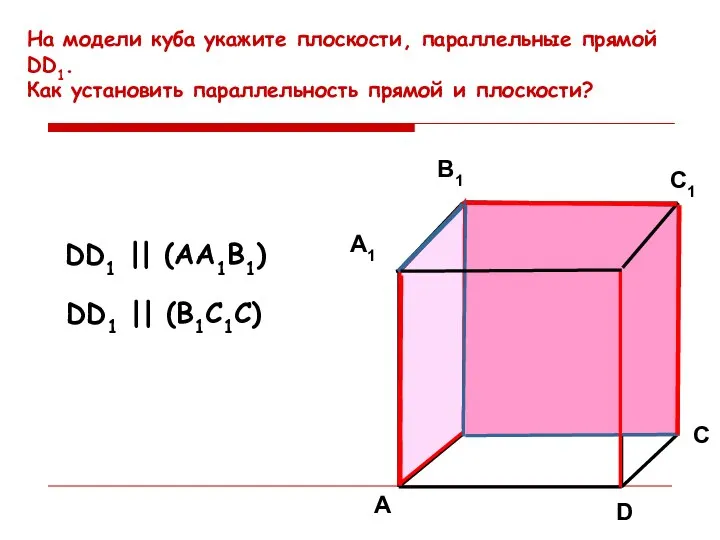
На модели куба укажите плоскости, параллельные прямой DD1.
Как установить параллельность прямой и плоскости?
C1
C
DD1 || (AA1B1)
DD1 || (B1C1C)

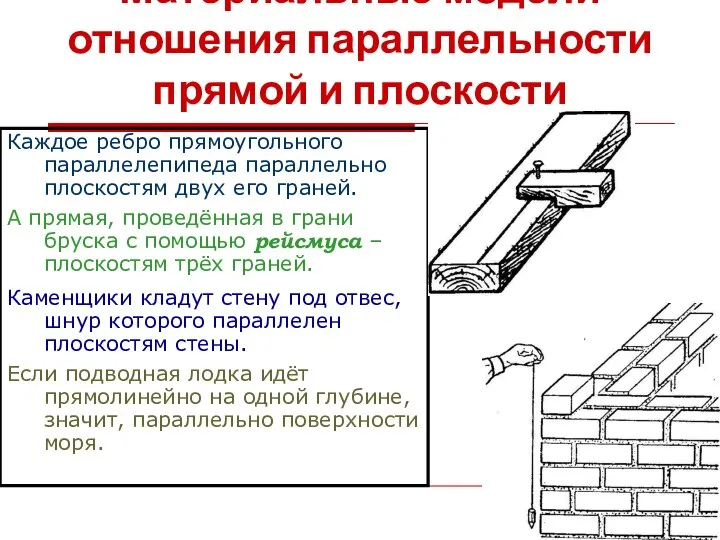
Материальные модели отношения параллельности прямой и плоскости
Каждое ребро прямоугольного параллелепипеда параллельно плоскостям двух его граней.
А прямая, проведённая в грани бруска с помощью рейсмуса – плоскостям трёх граней.
Каменщики кладут стену под отвес, шнур которого параллелен плоскостям стены.
Если подводная лодка идёт прямолинейно на одной глубине, значит, параллельно поверхности моря.

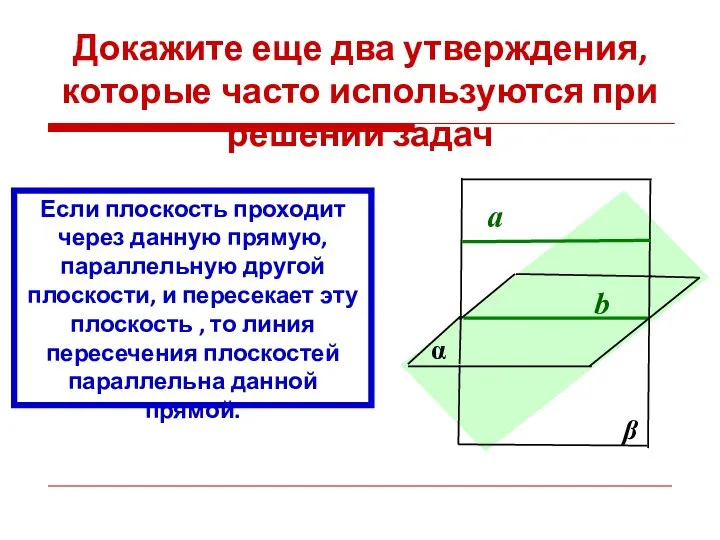
Докажите еще два утверждения, которые часто используются при решении задач
Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость , то линия пересечения плоскостей параллельна данной прямой.
α
β
а
b

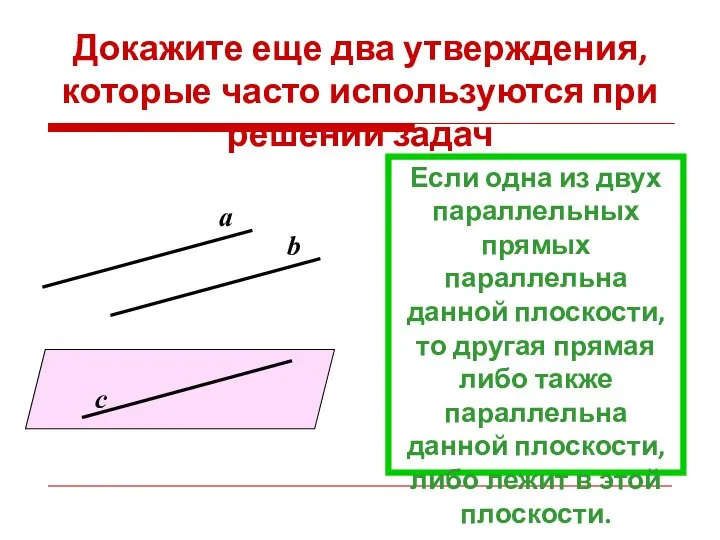
Докажите еще два утверждения, которые часто используются при решении задач
Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
а
b
с

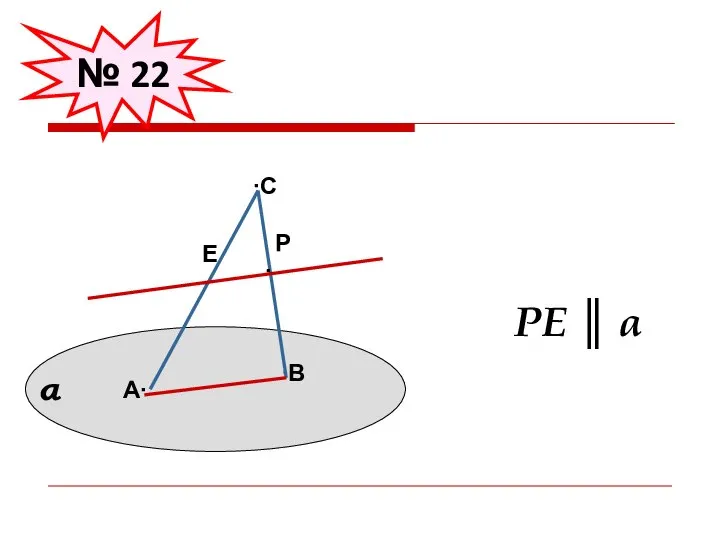
РЕ ║ α
№ 22
А∙
∙В
∙С
Е ∙
Р ∙
α

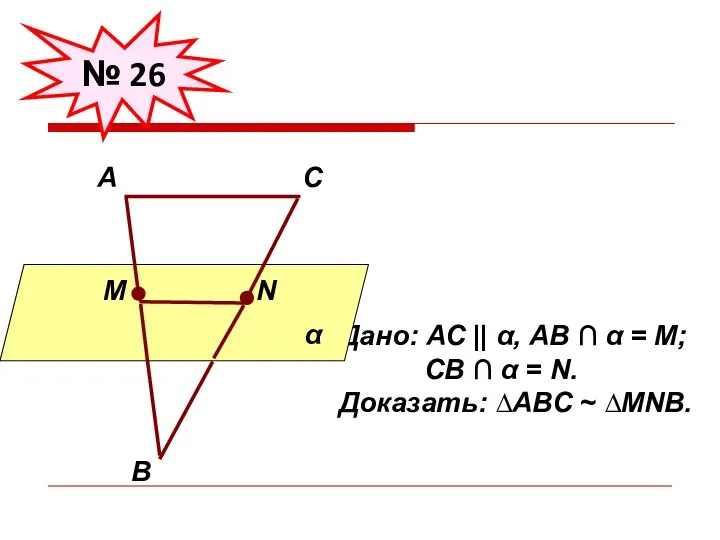
№ 26
Дано: АС || α, АВ ∩ α = М;
СВ ∩ α = N.
Доказать: ∆АВС ~ ∆МNВ.
α
А
С
В
М
N

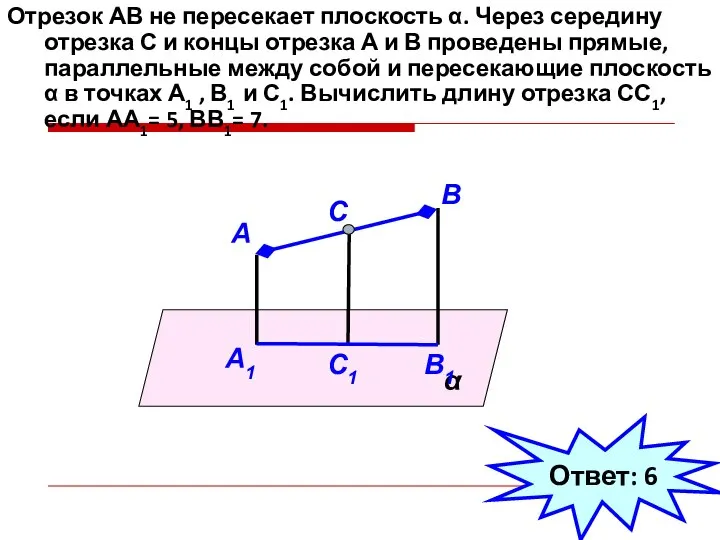
Отрезок АВ не пересекает плоскость α. Через середину отрезка С и концы отрезка А и В проведены прямые, параллельные между собой и пересекающие плоскость α в точках А1 , В1 и С1. Вычислить длину отрезка СС1, если АА1= 5, ВВ1= 7.
α
А
В
С
А1
В1
С1
Ответ: 6

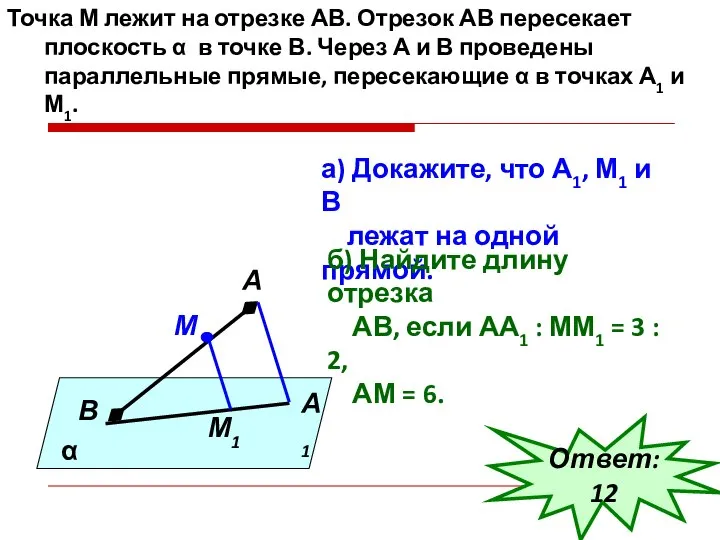
Точка М лежит на отрезке АВ. Отрезок АВ пересекает плоскость α в точке В. Через А и В проведены параллельные прямые, пересекающие α в точках А1 и М1.
α
А
В
М
А1
М1
а) Докажите, что А1, М1 и В
лежат на одной прямой.
б) Найдите длину отрезка
АВ, если АА1 : ММ1 = 3 : 2,
АМ = 6.
Ответ: 12

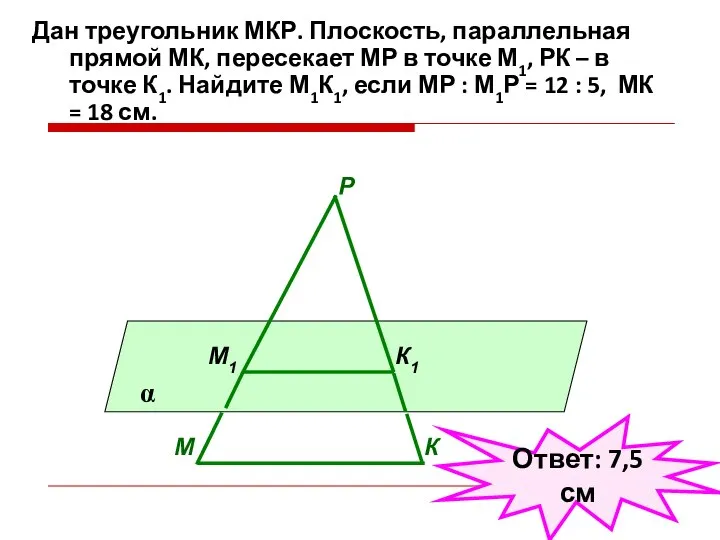
Дан треугольник МКР. Плоскость, параллельная прямой МК, пересекает МР в точке М1, РК – в точке К1. Найдите М1К1, если МР : М1Р = 12 : 5, МК = 18 см.
α
М
К
Р
М1
К1
Ответ: 7,5 см

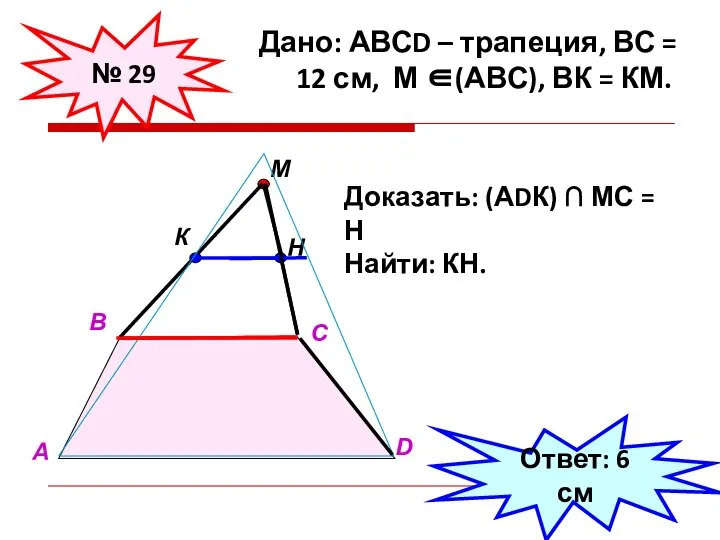
Дано: АВСD – трапеция, ВС = 12 см, М ∈(АВС), ВК = КМ.
№ 29
А
В
С
D
М
К
Доказать: (АDК) ∩ МС = Н
Найти: КН.
Н
Ответ: 6 см

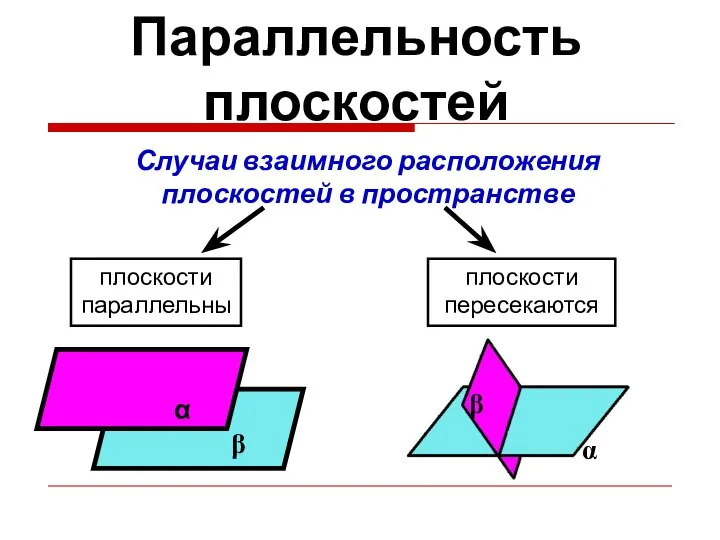
Параллельность плоскостей
Случаи взаимного расположения плоскостей в пространстве
плоскости параллельны
плоскости пересекаются
α
β

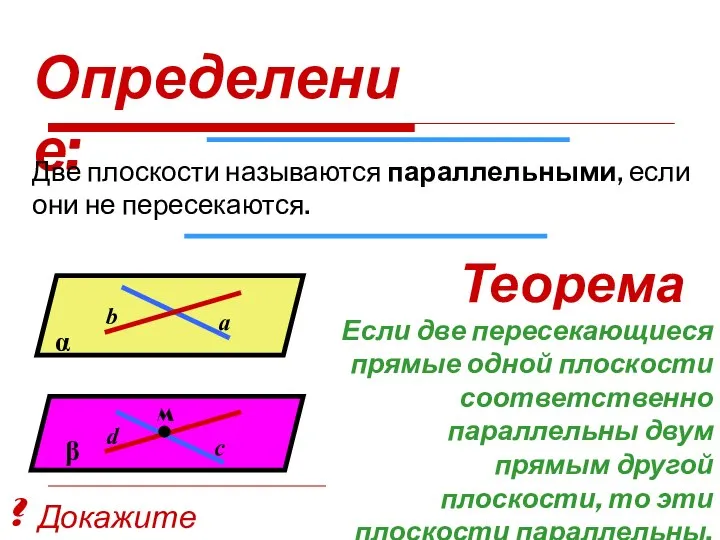
Определение:
Две плоскости называются параллельными, если они не пересекаются.
Теорема:
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Докажите теорему
?

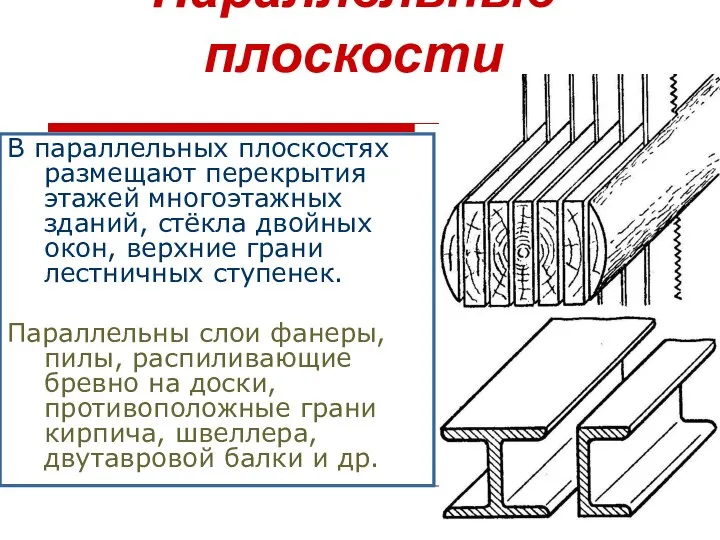
Параллельные плоскости
В параллельных плоскостях размещают перекрытия этажей многоэтажных зданий, стёкла двойных окон, верхние грани лестничных ступенек.
Параллельны слои фанеры, пилы, распиливающие бревно на доски, противоположные грани кирпича, швеллера, двутавровой балки и др.

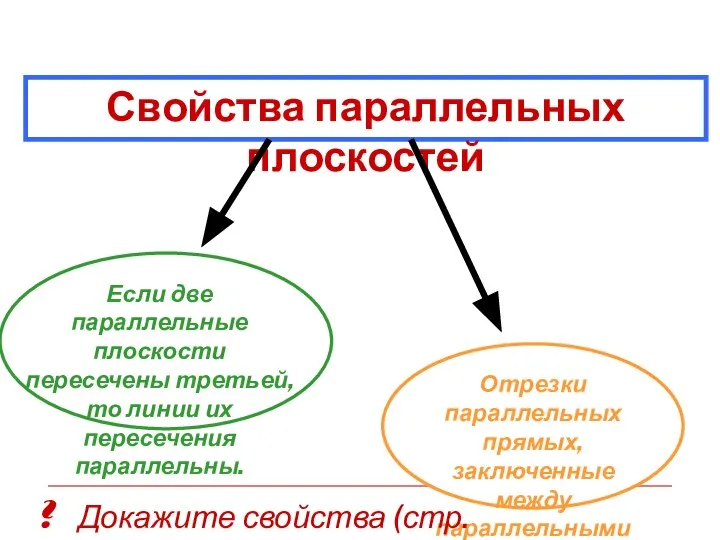
Свойства параллельных плоскостей
Докажите свойства (стр. 21)
?

А теперь небольшой тест!
Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны?
Точка М не лежит на прямой а. Сколько прямых, не пересекающих прямую а, проходит через точку М? Сколько из этих прямых параллельны прямой а?
Прямые а и с параллельны, а прямые a и b пересекаются. Могут ли прямые b и с пересекаться. Могут ли прямые b и c быть параллельны?
Прямая а параллельна плоскости α. Верно ли, что эта прямая не пересекает ни одну прямую, лежащую в плоскости α?
Прямая а параллельна плоскости α. Сколько прямых, лежащих в плоскости α, параллельны прямой а? Параллельны ли друг другу эти прямые, лежащие в плоскости α?
Могут ли быть равны два непараллельных отрезка, заключенные между параллельными плоскостями?
Две стороны параллелограмма параллельны плоскости α. Параллельны ли плоскость α и плоскость параллелограмма?

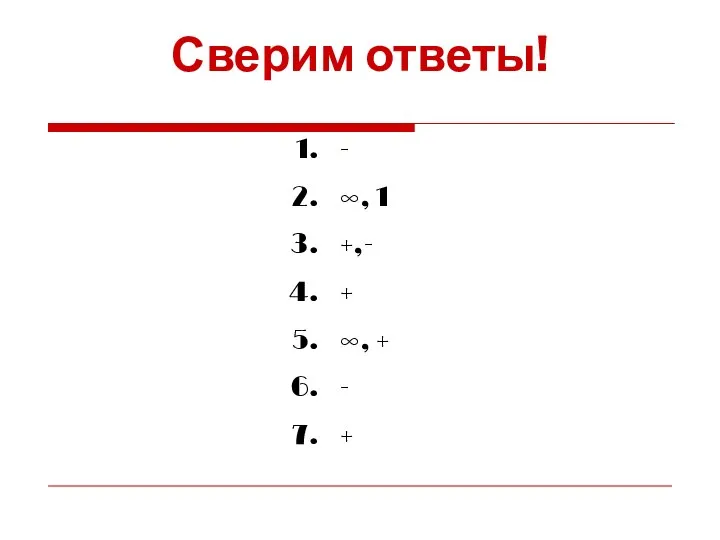
Сверим ответы!
-
∞, 1
+,-
+
∞, +
-
+