Содержание
- 2. Квадратное уравнение с действительными коэффициентами ?
- 3. На множестве С можно находить корни любых квадратных уравнений! Как извлечь квадратный корень из отрицательных действительных
- 4. Как извлечь квадратный корень из отрицательных действительных чисел? Определение: квадратным корнем(корнем второй степени) из комплексного числа
- 5. Формула извлечения квадратного корня из отрицательных действительных чисел
- 6. Решение квадратных уравнений с действительными коэффициентами и D Важно знать! Если у уравнения есть комплексный корень,
- 7. Как извлечь квадратный корень из любого комплексного числа? (в алгебраической и тригонометрической форме записи). Теорема: Если
- 8. Например:
- 9. Избежать громоздких вычислений позволяет тригонометрическая форма записи комплексного числа. Теорема: Доказательство: Всегда 2 корня!
- 10. = = = Аналогично: Важно запомнить! При возведении комплексного числа в квадрат – его аргумент удваивается!!!
- 11. Алгоритм извлечения квадратного корня из комплексного числа: Найти модуль ρ и аргумент α этого числа; Провести
- 12. 1). = = z 2 -2 1 -1 2)-4).
- 13. Решение квадратных уравнений с комплексными коэффициентами. Так как множества и совпадают между собой , то для
- 14. Полезные следствия для формулы корней квадратного уравнения: (теорема Виета) Если Z1 и Z2 –корни квадратного уравнения
- 16. Скачать презентацию













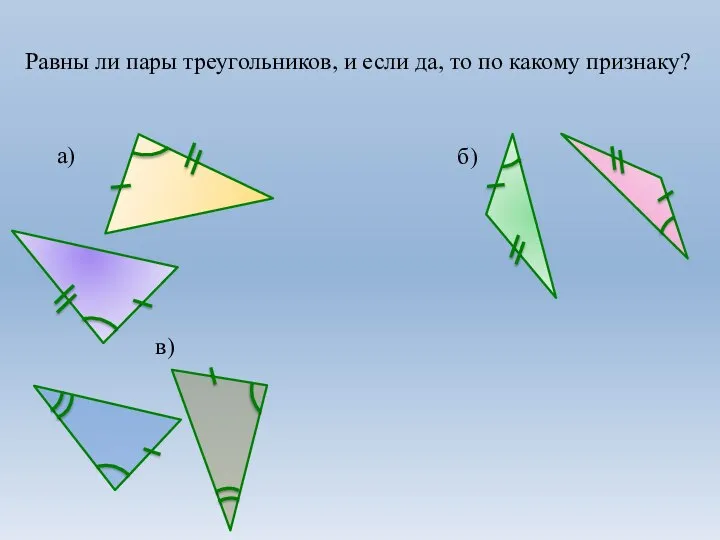 Второй признак равенства треугольников. 7 класс
Второй признак равенства треугольников. 7 класс Показательные функции
Показательные функции Решение задач с помощью составления систем уравнений. 9 класс
Решение задач с помощью составления систем уравнений. 9 класс Дискретная математика: теория алгоритмов и сложность вычислений
Дискретная математика: теория алгоритмов и сложность вычислений Основы логики
Основы логики Бином Ньютона
Бином Ньютона Решение задач на движение в противоположных направлениях
Решение задач на движение в противоположных направлениях Теория вероятностей, подготовка к ЕГЭ - 2019
Теория вероятностей, подготовка к ЕГЭ - 2019 Произведение событий. Условная вероятность. Теорема умножения вероятностей
Произведение событий. Условная вероятность. Теорема умножения вероятностей Prezentatsia_k_uroku_matematiki_v_6_kl
Prezentatsia_k_uroku_matematiki_v_6_kl Параллелограмм и трапеция. Урок 3
Параллелограмм и трапеция. Урок 3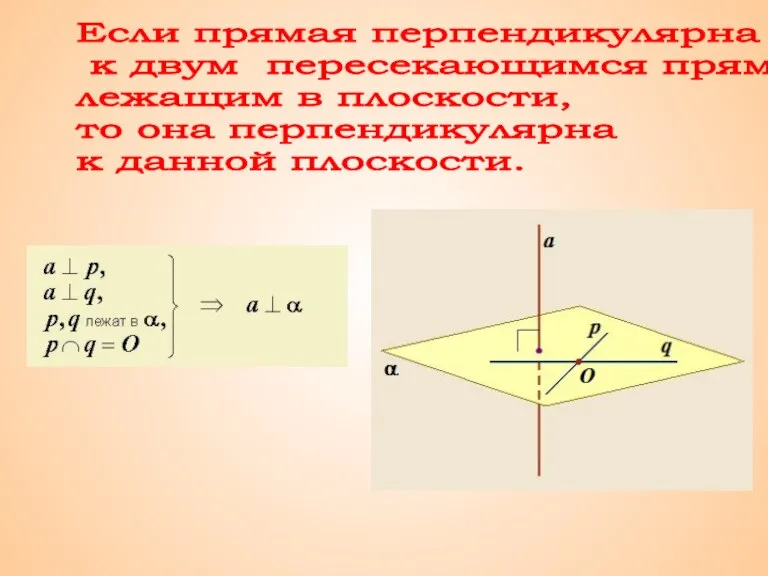 Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости История дробей
История дробей Математический магазин
Математический магазин Тест по теме Цилиндр
Тест по теме Цилиндр Презентация на тему Площадь прямоугольника: практикум
Презентация на тему Площадь прямоугольника: практикум  Кластерный анализ. Лекция 8
Кластерный анализ. Лекция 8 Возникновение комбинаторной теории
Возникновение комбинаторной теории Числовое значение буквенного выражения (часть 2)
Числовое значение буквенного выражения (часть 2) Презентация на тему Линейная функция 6 класс
Презентация на тему Линейная функция 6 класс  Игра-тренажер А знаете ли вы…. Математика 3 класс
Игра-тренажер А знаете ли вы…. Математика 3 класс Связь между суммой и слагаемыми (1 класс)
Связь между суммой и слагаемыми (1 класс) Параллельные прямые
Параллельные прямые Числа и точки на прямой. 5 класс
Числа и точки на прямой. 5 класс Funksiya. Funksiyaning berilish usullari
Funksiya. Funksiyaning berilish usullari Геометрические тела. 5 класс
Геометрические тела. 5 класс Тригонометрические уравнения
Тригонометрические уравнения Решение задач по теме Параллельность прямой и плоскости
Решение задач по теме Параллельность прямой и плоскости