Лекция 5. Плоские и планарные графы

ИЗОМОРФНЫЕ ГРАФЫ
Графы G' и G" называются изоморфными, если существует взаимно –однозначное соответствие между их ребрами и вершинами, причем соответствующие ребра соединяют соответствующие вершины.
Между названием вершины и ее номером различия нет. Можно так переобозначить вершины первого графа, что в новых обозначениях вершины и ребра будут совпадать со вторым графом, причем кратным ребрам первого G' должны соответствовать кратные ребра второго G" такой же кратности (рис. 5.1).
Рисунок 5.1 – Изоморфные графы

ДВА ГРАФА ИЗОМОРФНЫ ТОГДА И ТОЛЬКО ТОГДА, КОГДА ВЕРШИНЫ ОДНОГО ИЗ НИХ МОЖНО ПЕРЕНУМЕРОВАТЬ ТАК, ЧТОБЫ МАТРИЦА СМЕЖНОСТИ ЭТОГО ГРАФА СОВПАЛА С МАТРИЦЕЙ СМЕЖНОСТИ ВТОРОГО ГРАФА.

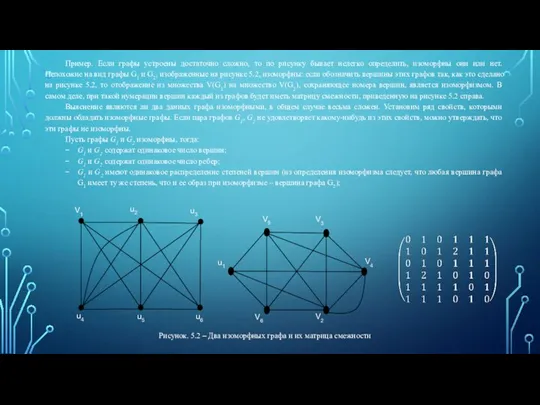
Рисунок. 5.2 – Два изоморфных графа и их матрица смежности
Пример. Если графы устроены достаточно сложно, то по рисунку бывает нелегко определить, изоморфны они или нет. Непохожие на вид графы G1 и G2, изображенные на рисунке 5.2, изоморфны: если обозначить вершины этих графов так, как это сделано на рисунке 5.2, то отображение из множества V(G1) на множество V(G2), сохраняющее номера вершин, является изоморфизмом. В самом деле, при такой нумерации вершин каждый из графов будет иметь матрицу смежности, приведенную на рисунке 5.2 справа.
Выяснение являются ли два данных графа изоморфными, в общем случае весьма сложен. Установим ряд свойств, которыми должны обладать изоморфные графы. Если пара графов G1, G2 не удовлетворяет какому-нибудь из этих свойств, можно утверждать, что эти графы не изоморфны.
Пусть графы G1 и G2 изоморфны, тогда:
G1 и G2 содержат одинаковое число вершин;
G1 и G2 содержат одинаковое число ребер;
G1 и G2 имеют одинаковое распределение степеней вершин (из определения изоморфизма следует, что любая вершина графа G1 имеет ту же степень, что и ее образ при изоморфизме – вершина графа G2);

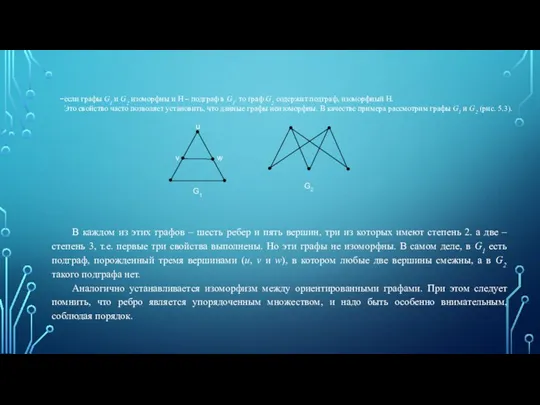
если графы G1 и G2 изоморфны и Н – подграф в G1. то граф G2 содержит подграф, изоморфный Н.
Это свойство часто позволяет установить, что данные графы неизоморфны. В качестве примера рассмотрим графы G1 и G2 (рис. 5.3).
Рисунок 5.3 – Неизоморфные графы
В каждом из этих графов – шесть ребер и пять вершин, три из которых имеют степень 2. а две – степень 3, т.е. первые три свойства выполнены. Но эти графы не изоморфны. В самом деле, в G1 есть подграф, порожденный тремя вершинами (и, v и w), в котором любые две вершины смежны, а в G2 такого подграфа нет.
Аналогично устанавливается изоморфизм между ориентированными графами. При этом следует помнить, что ребро является упорядоченным множеством, и надо быть особенно внимательным, соблюдая порядок.

ПЛОСКИЕ И ПЛАНАРНЫЕ ГРАФЫ
Граф, изображенный на плоскости, называется плоским, если его ребра не пересекаются в точках, отличных от вершин графа.
Свойство «быть плоским» может не сохраняться при переходе к изоморфному графу. Например, графы G1 и G2 (рис. 5.4), изоморфны. Но граф G1 является плоским, а граф G2 – нет.
Плоские и планарные графы
G1 G2
Рисунок 5.4 – Свойства плоскости

Граф называется планарным, если он изоморфен плоскому графу. Граф G2 на рисунке 5.4 является планарным, но не плоским.
Плоский граф называется максимально плоским, если невозможно добавить к нему ни одного ребра так, чтобы полученный граф был плоским
Рисунок 5.5 – Максимальный и не максимально плоский графы
Каждая грань в плоском представлении максимально плоского графа имеет 3 вершины. Поэтому максимально плоский граф называют еще триангулированным. Операция добавления новых ребер, в результате которой в плоском представлении каждая грань имеет ровно 3 вершины, называется триангуляцией графа. Триангулированные графы с одним и тем же числом вершин могут не совпадать.

УКЛАДКА ГРАФА НА ПОВЕРХНОСТИ
Понятия плоского и планарного графа являются частными случаями следующих более общих понятий.
Пусть σ – произвольная поверхность в трехмерном пространстве. Граф G, изображенный на поверхности σ, называется уложенным на σ, если его ребра не пересекаются в точках, отличных от вершин. Граф G укладывается на поверхности σ, если он изоморфен некоторому графу, уложенному на σ.
Свойство графа укладываться на поверхности безусловно зависит от вида этой поверхности. Однако многие поверхности с точки зрения укладки графов ничем не отличаются от плоскости. Принципиально важен следующий случай.
Теорема об укладке графа на сфере. Граф укладывается на сфере тогда и только тогда, когда он планарен.

Гранью плоского графа называется максимальная область плоскости, любые две точки которой можно соединить непрерывной линией, не пересекающей граф (точки графа не принадлежат никакой грани). Т.е. грань в плоском представлении графа G называется часть плоскости, ограниченная простым циклом и не содержащая внутри других циклов. Тем самым каждая точка плоскости принадлежит хотя бы одной грани плоского графа.
Число граней плоского графа G обозначается через g(G).
Замечание. Любой плоский граф содержит ровно одну неограниченную грань (иными словами, грань бесконечной площади). Эта грань называется внешней.

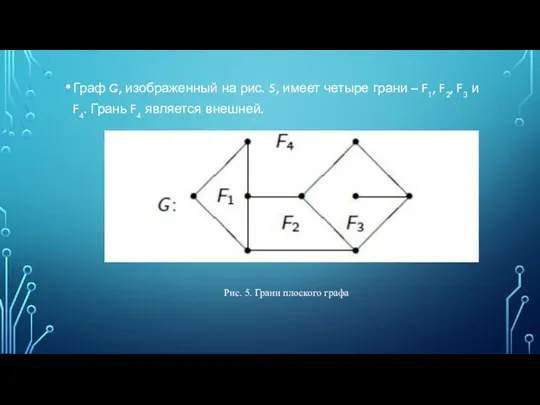
Граф G, изображенный на рис. 5, имеет четыре грани – F1, F2, F3 и F4. Грань F4 является внешней.
Рис. 5. Грани плоского графа

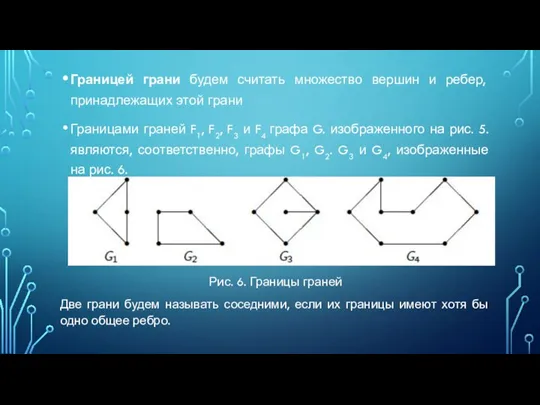
Границей грани будем считать множество вершин и ребер, принадлежащих этой грани
Границами граней F1, F2, F3 и F4 графа G. изображенного на рис. 5. являются, соответственно, графы G1, G2. G3 и G4, изображенные на рис. 6.
Рис. 6. Границы граней
Две грани будем называть соседними, если их границы имеют хотя бы одно общее ребро.

ФОРМУЛА ЭЙЛЕРА
Если обыкновенный связный плоский граф имеет п вершин, m ребер и r граней, то
n - m + r = 2.
Замечание. Равенство
n - m + r = 2
из формулировки теоремы называется тождеством Эйлера.

СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ ЭЙЛЕРА
1. Следствие об изоморфизме
Два изоморфных плоских графа имеют одинаковое число граней.
Таким образом, у всех плоских изображений заданного планарного графа будет одно и то же число граней.
2. Следствие о несвязных графах
Если обыкновенный плоский граф G имеет п вершин, m ребер, r граней и с компонент связности, то
n - m + r = с + 1.

3. Следствие о числе ребер
Если обыкновенный связный планарный граф G содержит n вершин и m ребер и n ≥ З, то
m ≤ Зn - 6.
4. Следствие о графе К5
Граф К5 не планарен. (Полный граф с n вершинами обозначается через Кn.)
Доказательство. Граф К5 содержит 5 вершин и 10 ребер. Поскольку неравенство 10 ≤ 3 • 5 - 6 неверно, этот граф не планарен по следствию о числе ребер.
5. Следствие о графе К3,3
Граф К3,3 не планарен.

КРИТЕРИИ ПЛАНАРНОСТИ.
Если граф является планарным, это можно доказать, предъявив соответствующее плоское изображение. Гораздо сложнее доказать, что граф планарным не является (головоломка о домах и колодцах служит тому хорошим примером). Теорема Эйлера и ее следствия позволяют в некоторых случаях доказывать непланарность графов.
Замечание о непланарных подграфах
Если у графа G есть непланарный подграф, то G не планарен.
Однако непланарность многих графов только этими способами доказать нельзя. Нужен критерий, позволяющий доказать непланарность любого непланарного графа. Рассмотрим два варианта такого критерия. Оба они демонстрируют, что графы К5 и К3,3, являются в некотором смысле «универсальными» непланарными графами.
Введем две новые операции над графами

Пусть и и v – смежные вершины графа G. Удалим из графа G ребро (и, v). а затем добавим к полученному графу новую вершину w и два новых ребра: (u,w) и (v,w) (см. рис. 7). Полученный после этого граф обозначим через G'. Говорят, что граф G' получен добавлением вершины степени 2 к графу G.
Рис. 7. Добавление вершины степени 2

Пусть w – вершина графа G, степень которой равна 2. Обозначим вершины, смежные с w в G, через и и v. Удалим из графа G вершину w, а затем добавим к полученному графу ребро (и, v) (см. рис. 8). Полученный граф обозначим через G'. Говорят, что граф G' получен стиранием вершины степени 2 в графе G.
Рис. 8. Стирание вершины степени 2

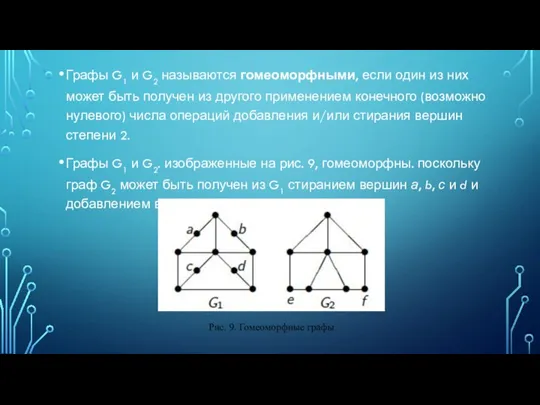
Графы G1 и G2 называются гомеоморфными, если один из них может быть получен из другого применением конечного (возможно нулевого) числа операций добавления и/или стирания вершин степени 2.
Графы G1 и G2. изображенные на рис. 9, гомеоморфны. поскольку граф G2 может быть получен из G1 стиранием вершин а, b, с и d и добавлением вершин е и f.
Рис. 9. Гомеоморфные графы

ТЕОРЕМА ПОНТРЯГИНА— КУРАТОВСКОГО
Обыкновенный граф G планарен тогда и только тогда, когда он не содержит подграфа, гомеоморфного одному из графов К5 и К3,3.
Пример. Покажем, как с помощью теоремы Понтрягина-Куратовского можно доказать непланарность графа. Рассмотрим граф, изображенный на рис. 10 слева (так называемый граф Петерсена).
Удалив из этого графа ребра (z1, z4) и (z2, z3), получаем граф G1. изображенный на рис. 10 посередине. Таким образом, G1 – подграф графа Петерсена. Граф G1 изоморфен графу G2, изображенному на рис. 10 справа. Очевидно, что граф G2 получается из графа К3,3 добавлением четырех вершин степени 2 (а именно, вершин z1, z2, z3 и z4). В силу теоремы Понтрягина-Куратовского граф Петерсена не планарен.

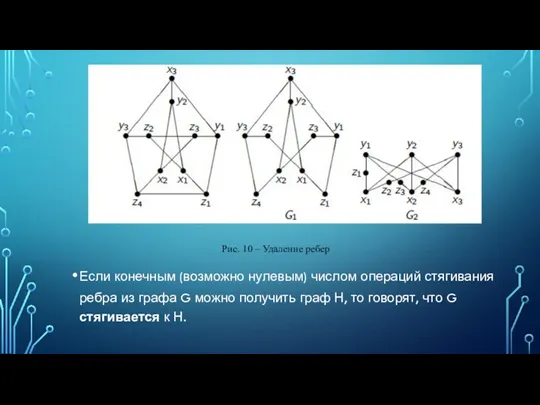
Если конечным (возможно нулевым) числом операций стягивания ребра из графа G можно получить граф Н, то говорят, что G стягивается к Н.
Рис. 10 – Удаление ребер

ТЕОРЕМА ВАГНЕРА
Обыкновенный граф G планарен тогда и только тогда, когда он не содержит подграфа, который стягивается к графу К5 или графу К3,3.
Пример. Покажем, как с помощью второго критерия планарности можно доказать непланарность графа. Рассмотрим вновь граф Петерсена и обозначим его вершины так, как это сделано на рис. 11 слева. Стягиванием ребра (a1, b1) получим граф, изображенный на рис. 11 посередине. Затем последовательно стянем ребра (a2, b2), (a3, b3). (a4, b4) и, наконец, (a5, b5). В результате получим граф, изображенный на рис. 11 справа, т.е. граф К5. Применяя теорему Вагнера, убеждаемся в том, что граф Петерсена не планарен.

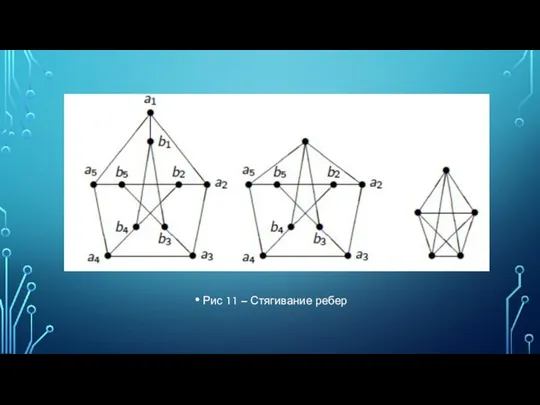
Рис 11 – Стягивание ребер