Содержание
- 2. Впервые понятие «граф» ввел в 1936 г. венгерский математик Денни Кёниг. Но первая работа по теории
- 3. Графом G = (V, X) называется пара двух конечных множеств: множество точек и множество линий, соединяющих
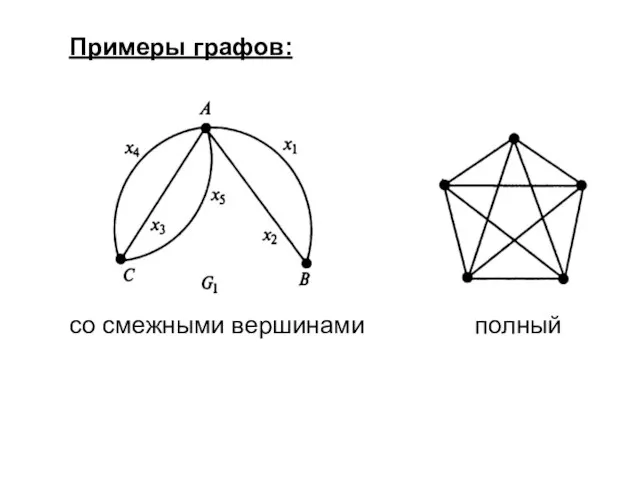
- 4. Примеры графов: со смежными вершинами полный
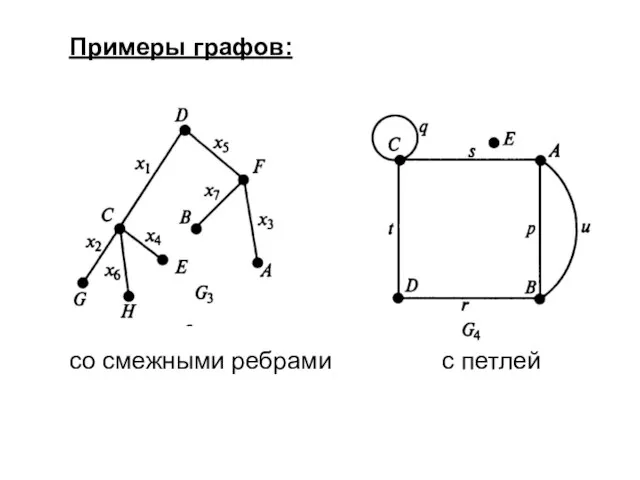
- 5. Примеры графов: со смежными ребрами с петлей
- 6. Пусть дан граф G = (V, X), где V = {V, W, ...} — конечное непустое
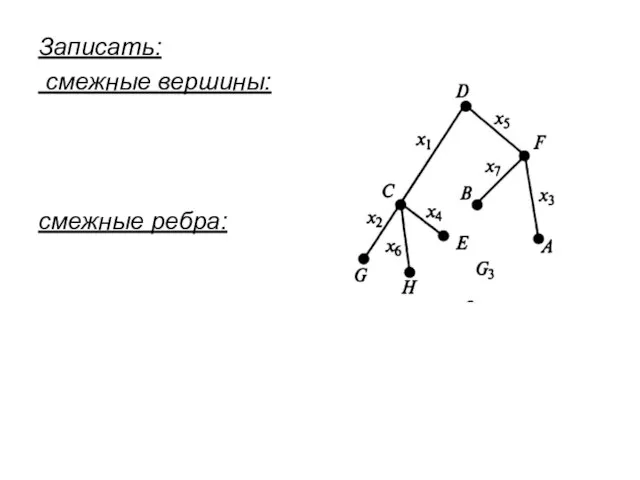
- 7. Записать: смежные вершины: смежные ребра:
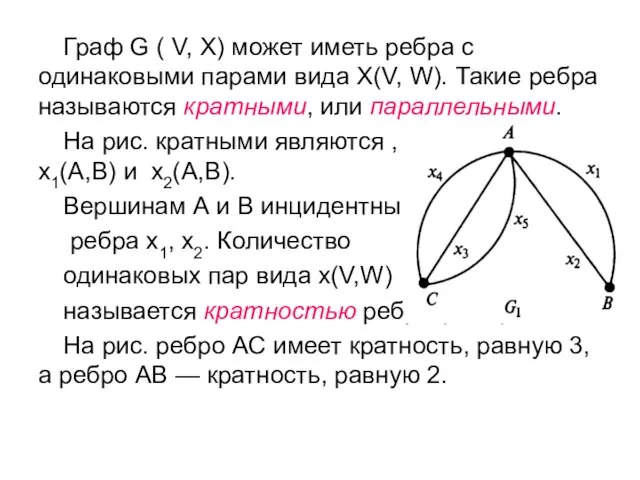
- 8. Граф G ( V, X) может иметь ребра с одинаковыми парами вида X(V, W). Такие ребра
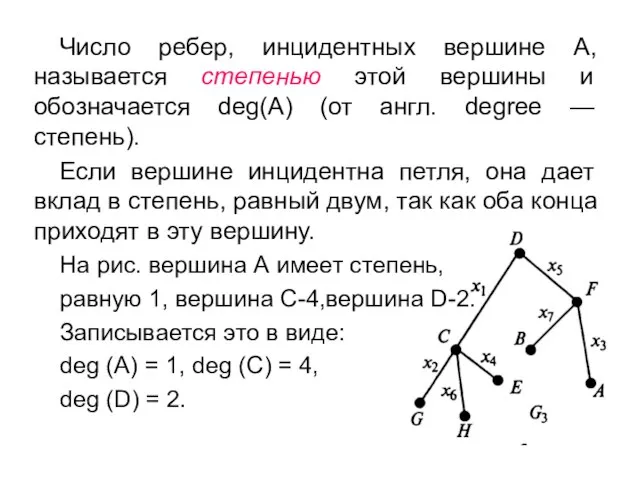
- 9. Число ребер, инцидентных вершине А, называется степенью этой вершины и обозначается deg(A) (от англ. degree —
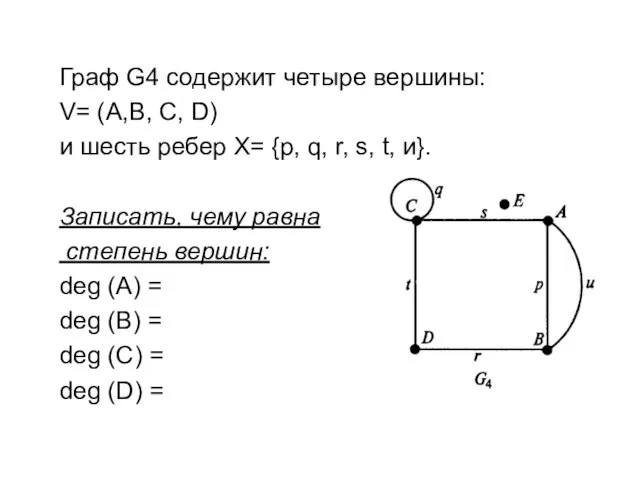
- 10. Граф G4 содержит четыре вершины: V= (A,В, С, D) и шесть ребер Х= {р, q, r,
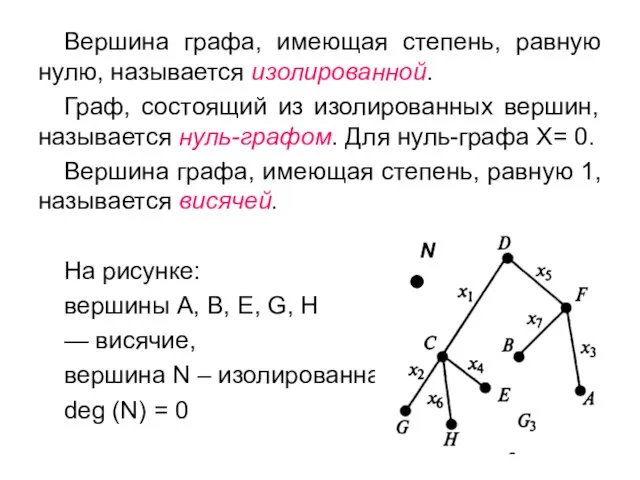
- 11. Вершина графа, имеющая степень, равную нулю, называется изолированной. Граф, состоящий из изолированных вершин, называется нуль-графом. Для
- 12. Теорема 2.1. В графе G(V,X) сумма степеней всех его вершин — число четное, равное удвоенному числу
- 13. Теорема 2.2. Число нечетных вершин любого графа — четно. Следствие. Невозможно начертить граф с нечетным числом
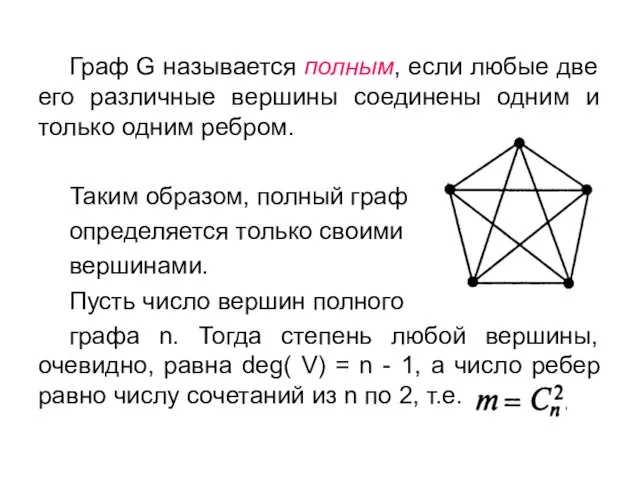
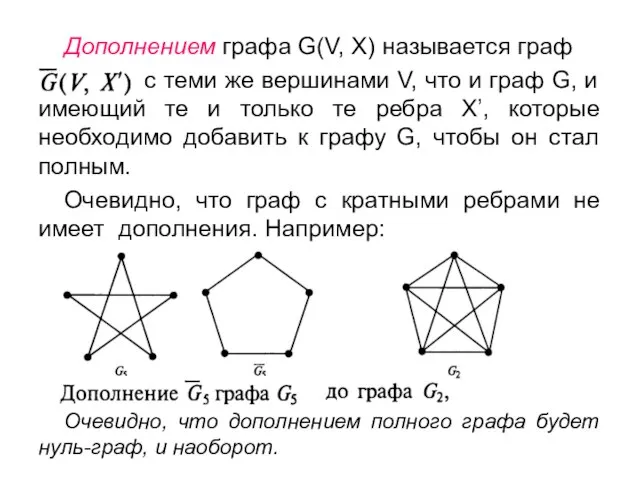
- 14. Граф G называется полным, если любые две его различные вершины соединены одним и только одним ребром.
- 15. Дополнением графа G(V, X) называется граф с теми же вершинами V, что и граф G, и
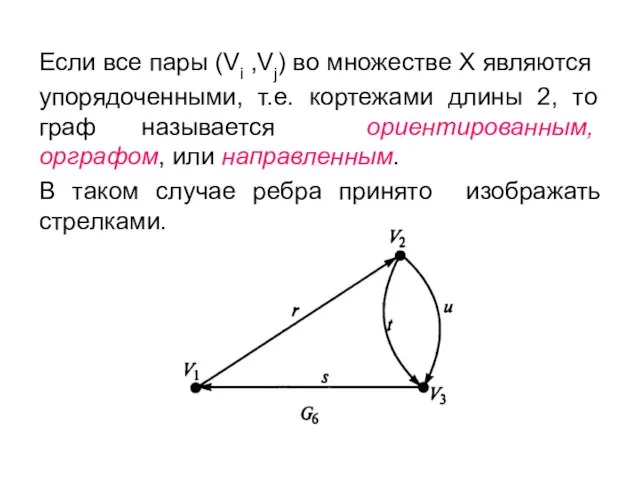
- 16. Если все пары (Vi ,Vj) во множестве X являются упорядоченными, т.е. кортежами длины 2, то граф
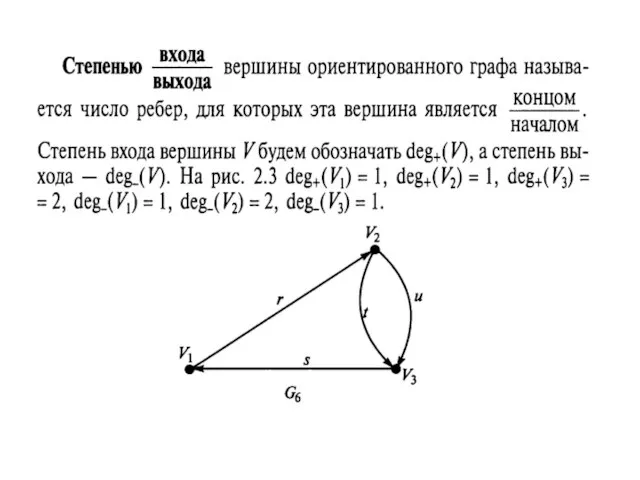
- 17. Началом ребра называется вершина, указанная в кортеже первой, концом — вторая вершина этой пары (графически она
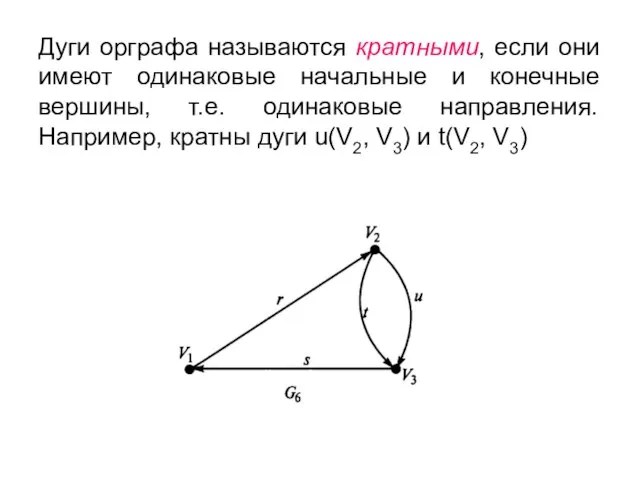
- 19. Дуги орграфа называются кратными, если они имеют одинаковые начальные и конечные вершины, т.е. одинаковые направления. Например,
- 20. Последовательность попарно инцидентных вершин Vi1 ,Vi2, ..., Vik неориентированного графа, т.е. последовательность ребер неориентированного графа, в
- 21. Расстоянием между двумя вершинами называется минимальная длина из всех возможных маршрутов между этими вершинами при условии,
- 23. Скачать презентацию








 Вычисление вероятностей событий с использованием формулы полной вероятности и формулы Байеса
Вычисление вероятностей событий с использованием формулы полной вероятности и формулы Байеса Квадратный корень и его свойства
Квадратный корень и его свойства Декартова система координат
Декартова система координат Узоры и орнаменты на посуде
Узоры и орнаменты на посуде Функция y = tg x её свойства и график
Функция y = tg x её свойства и график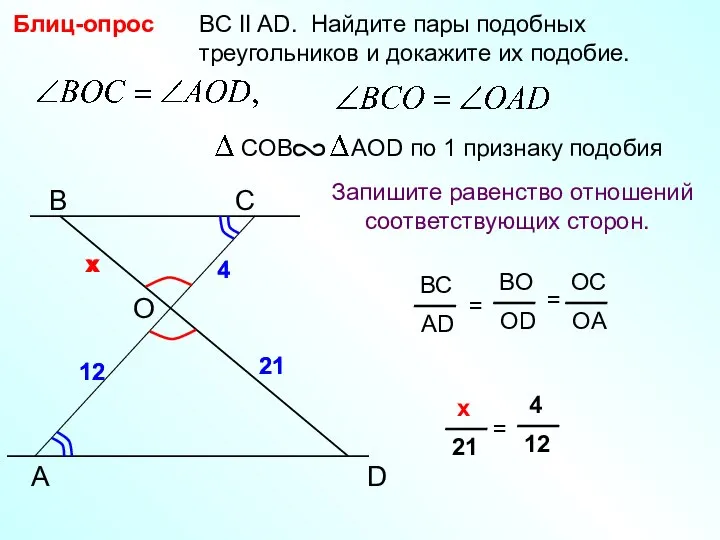 Признаки подобия треугольников
Признаки подобия треугольников Произведение чисел
Произведение чисел Обыкновенные дроби. Эти таежные животные
Обыкновенные дроби. Эти таежные животные Табличные случаи сложения и вычитания с переходом через разряд в пределах 20
Табличные случаи сложения и вычитания с переходом через разряд в пределах 20 Формула Ньютона-Лейбница. Площадь криволинейной трапеции
Формула Ньютона-Лейбница. Площадь криволинейной трапеции Равнобедренный треугольник
Равнобедренный треугольник Треугольник
Треугольник Умножение с опорным числом
Умножение с опорным числом Типовой расчет по дискретной математике
Типовой расчет по дискретной математике Производная функции. Геометрический смысл производной. Механический смысл производной
Производная функции. Геометрический смысл производной. Механический смысл производной Задания
Задания Подумай. Вопросы. Тесты
Подумай. Вопросы. Тесты Презентация по математике "Устные приёмы сложения и вычитания в пределах 100" -
Презентация по математике "Устные приёмы сложения и вычитания в пределах 100" -  Параллельность плоскостей. Лекция 4
Параллельность плоскостей. Лекция 4 Равнобедренный треугольник и его свойства, 7 класс
Равнобедренный треугольник и его свойства, 7 класс Задача Магницкого
Задача Магницкого Многогранники
Многогранники Решение задач на нахождение объемов и площадей поверхностей тел
Решение задач на нахождение объемов и площадей поверхностей тел Задача № 5 з математики. Команда “Леонардо”
Задача № 5 з математики. Команда “Леонардо” Решение задач ( 8 класс)
Решение задач ( 8 класс) Квадратное уравнение и его корни
Квадратное уравнение и его корни Презентация на тему ЗАДАНИЯ С РАЗВЕРНУТЫМ ОТВЕТОМ ПОВЫШЕННОГО УРОВНЯ СЛОЖНОСТИ С5. ПОДГОТОВКА К ЕГЭ
Презентация на тему ЗАДАНИЯ С РАЗВЕРНУТЫМ ОТВЕТОМ ПОВЫШЕННОГО УРОВНЯ СЛОЖНОСТИ С5. ПОДГОТОВКА К ЕГЭ  Парабола и ее свойства
Парабола и ее свойства