Содержание
- 2. Пары задают соответствие между множествами A и B, если указано правило R, по которому для элемента
- 3. Соответствия Соответствие между множествами А и В определяется заданным правилом, согласно которому элементам одного множества сопоставляются
- 4. Пусть ϕ ⊂ A × B и ϕ : A → B, тогда Область определения соответствия
- 5. Пример: Пусть дано множество студентов: A = {Jüri, Mari, Jaan, Juhan, Kati, Mati} и множество возможных
- 6. Пусть даны множества А и В А = { 2, 3, 8 } В = {
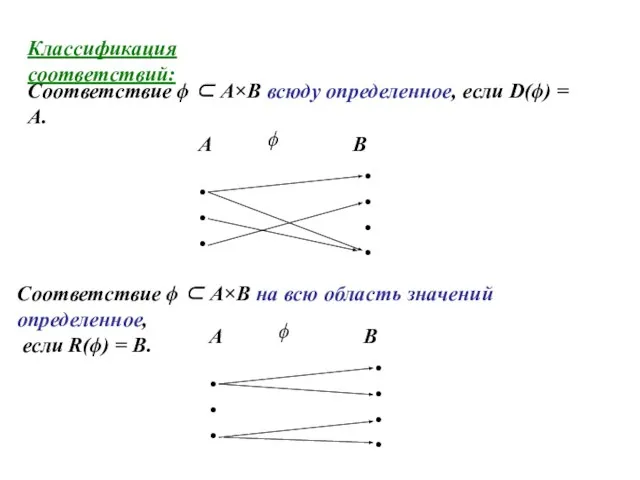
- 7. Классификация соответствий: Соответствие ϕ ⊂ A×B всюду определенное, если D(ϕ) = A. Соответствие ϕ ⊂ A×B
- 8. ϕ -1 ° ϕ = { (b,b) | b∈B } Соответствие ϕ ⊂ A×B однозначное, если
- 9. Образ множества A при соответствии R называется множеством значений этого соответствия и обозначается , если состоит
- 10. Для описания соответствий между множествами используют понятие отображения (функции) одного множества на другое.
- 11. Функциональные БО Бинарное отношение называется функциональным, если каждому элементу x из X такому, что соответствует один
- 12. Функция (отображение) Определение Всюду определенное функциональное отношение называется называется функцией или отображением множества X в Y:
- 13. Пример А={1,2,3}, B={e,f,g} G={(1,e), (2,e)} ⊆ A×B Образы и прообразы G образы прообразы
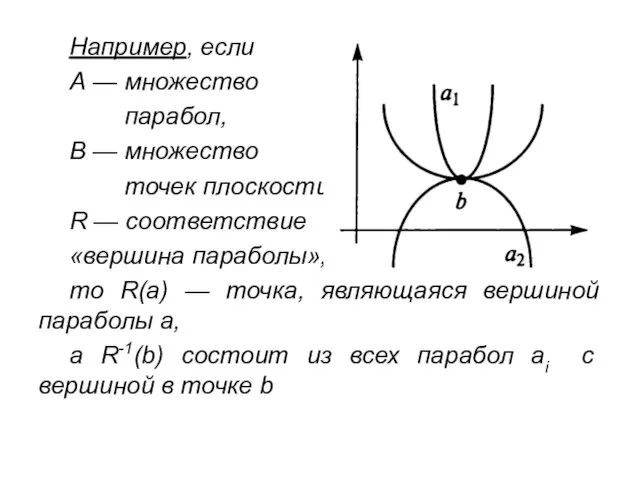
- 14. Например, если А — множество парабол, В — множество точек плоскости, R — соответствие «вершина параболы»,
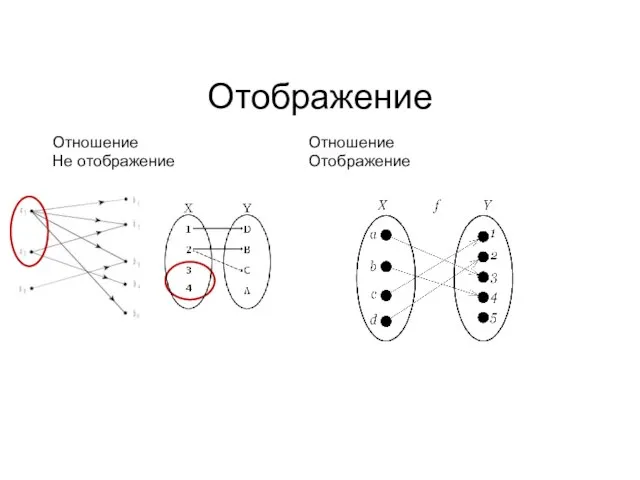
- 15. Отображение Отношение Отношение Не отображение Отображение
- 16. Функция. Пример. Пусть А = {-2, -1, 0, 1, 2}, a B = {0, 1, 2,
- 17. Функция. Пример. Пусть А = {-2, -1, 0, 1, 2} и В = {0, 1, 2,
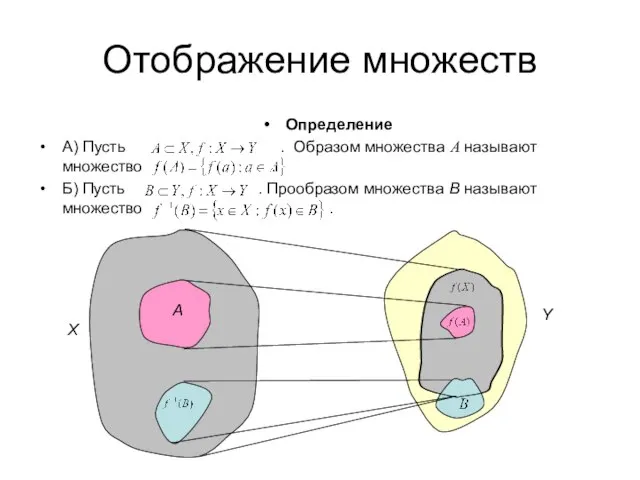
- 18. Отображение множеств Определение А) Пусть . Образом множества A называют множество . Б) Пусть . Прообразом
- 19. Задание отображений. Для задания отображения необходимо указать: • множество, которое отображается (область определения данного отображения D(f));
- 20. При записи подразумевается, что отображение f определено всюду на A, т.е. A – полный прообраз отображения
- 21. Способ задания отображений в виде формул называется аналитическим. Существуют еще табличный и графический способы. Для задания
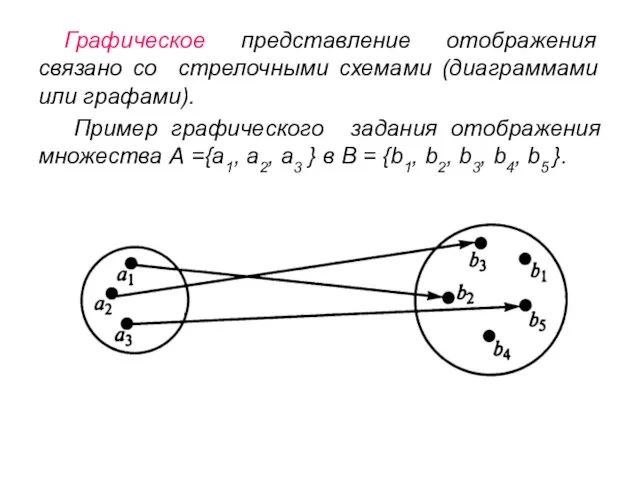
- 22. Графическое представление отображения связано со стрелочными схемами (диаграммами или графами). Пример графического задания отображения множества А
- 23. Отображения f: А ? В и g: A ? В называются равными, если Отображения называются однозначными,
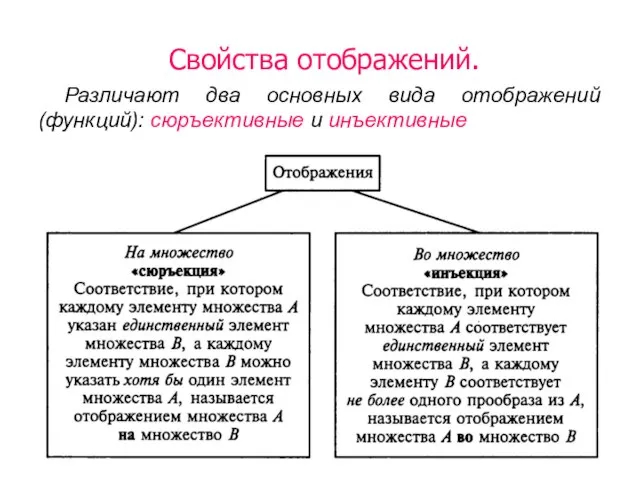
- 24. Свойства отображений. Различают два основных вида отображений (функций): сюръективные и инъективные
- 25. свойства Определения Отображение называется сюръективным, если . Б) Отображение называется инъективным, если для любых справедлива импликация
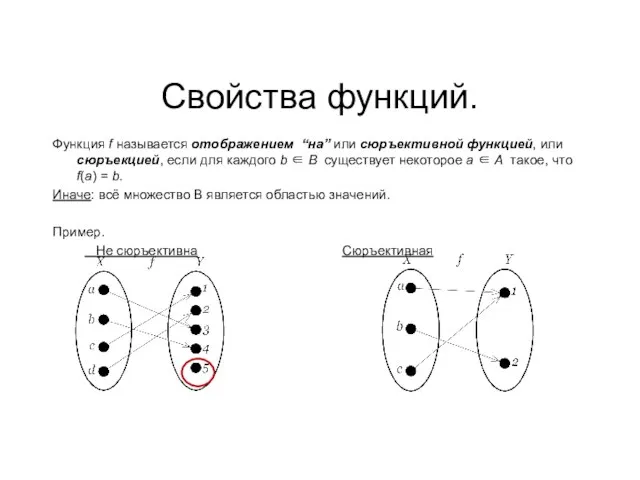
- 26. Свойства функций. Функция f называется отображением “на” или сюръективной функцией, или сюръекцией, если для каждого b
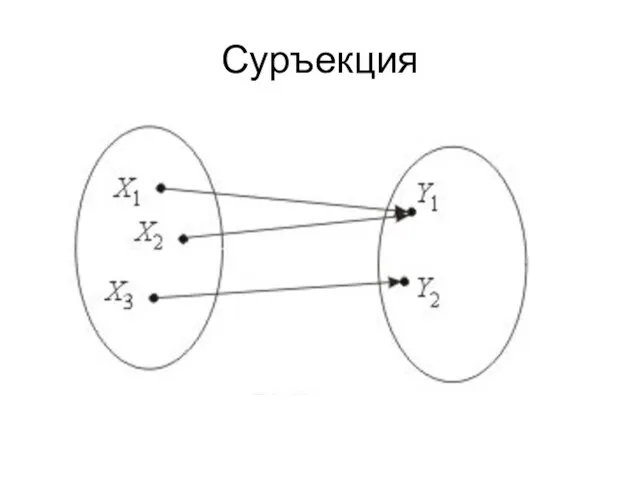
- 27. Суръекция
- 28. Сюръекция Соответствие между множеством всех студентов и множеством групп – сюръективное отображение, так как каждой группе
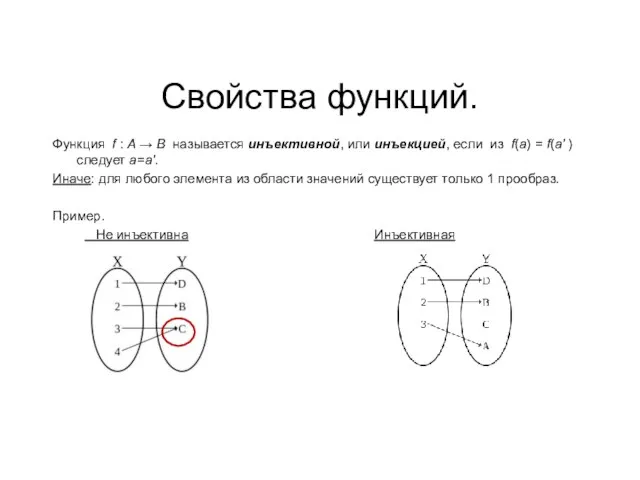
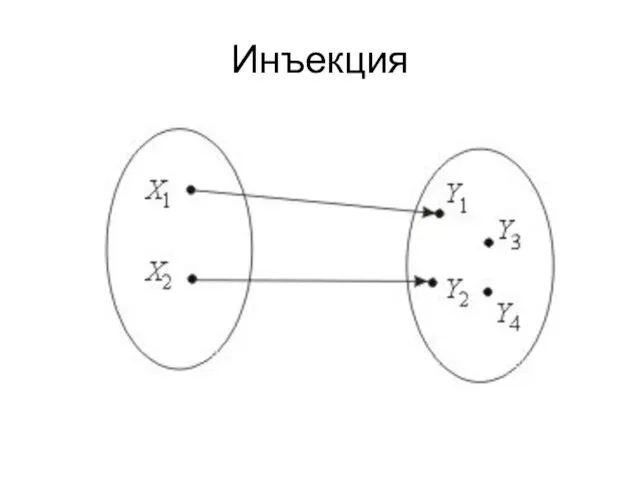
- 29. Свойства функций. Функция f : A → B называется инъективной, или инъекцией, если из f(a) =
- 30. Инъекция
- 31. Инъекция Отображение множества студентов данной аудитории на множество стульев - инъекция, так как разные студенты сидят
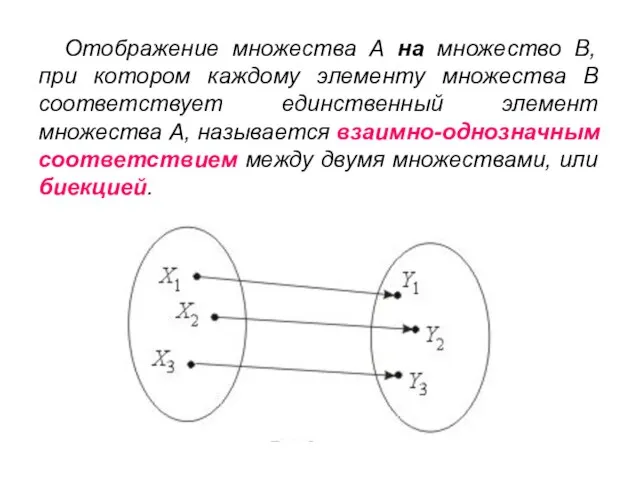
- 32. Отображение множества А на множество В, при котором каждому элементу множества В соответствует единственный элемент множества
- 33. Свойства функций. Функция, которая является одновременно и инъективной, и сюръективной, называется взаимно однозначным соответствием, или биекцией.
- 34. Биекция Примеры Соответствие между множеством государств Европы и множеством европейских столиц - биекция 2) Соответствие между
- 35. Свойства функций. Пример. Пусть А и В - множества действительных чисел и f : A →
- 36. Свойства функций. Пример. Пусть А и В – множество действительных чисел, и функция f : A
- 37. Обратная функция. Пусть f – функция из множества А во множество В, то есть f :
- 38. Обратная функция. Пример. Требуется найти обратную функцию для y = 3x + 6. Обращая функцию, получается
- 39. Два множества эквивалентны, если между их элементами можно установить биективное отображение. Это обозначается следующим образом: A
- 40. Пусть множество А отображается взаимно-однозначно на множество В, т.е f:А?В. Тогда отображение f -1, при котором
- 41. Если между элементами множеств установлено взаимно-однозначное соответствие, то эти множества имеют одинаковое количество элементов. Говорят, что
- 42. Рассмотрим примеры отображений. 1) Каждому действительному числу поставим в соответствие его квадрат. Отображение х?х2 не является
- 43. Рассмотрим примеры отображений. 2) Англо-русский словарь устанавливает соответствие между множествами слов английского и русского языков. Такое
- 44. Рассмотрим примеры отображений. 3) Различные виды кодирования (азбука Морзе, представление чисел в различных системах счисления, шифрованные
- 45. Отображение е: А ? А называется тождественным (единичным), если каждому аргументу оно ставит в соответствие себя.
- 46. Обратная функция. Теорема 1. 1) Если f : A → B является биекцией. То обратное отношение
- 47. Обратная функция. Теорема 2. Если f : A → B является биекцией, то a) f (f
- 48. Обратная функция. Теорема 3. Если f : A → A и I - тождественная функция на
- 49. Композиция функций. Пусть заданы отображения f1: А?В и f2: B?C. Отображение f: А?C, при котором каждому
- 50. Композиция функций. Теорема: Пусть g : A → B и f: B → C. Тогда а)
- 51. Композиция функций. Примеры.
- 52. Композиция функций. Теорема. Пусть g : A → B f : B → C . Тогда
- 53. Повторение
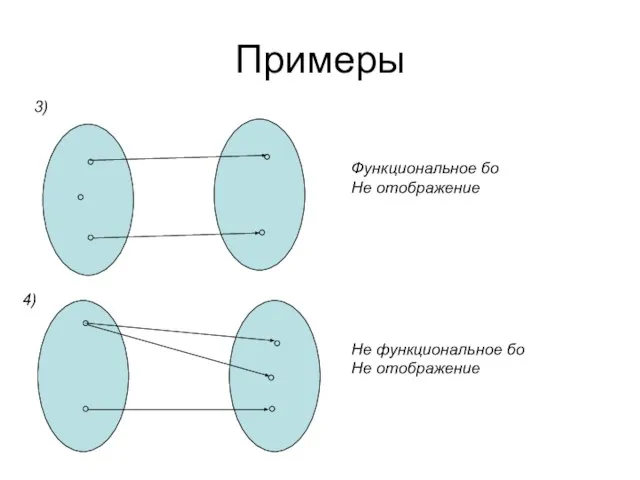
- 54. Примеры Функциональное бо Не отображение Не функциональное бо Не отображение
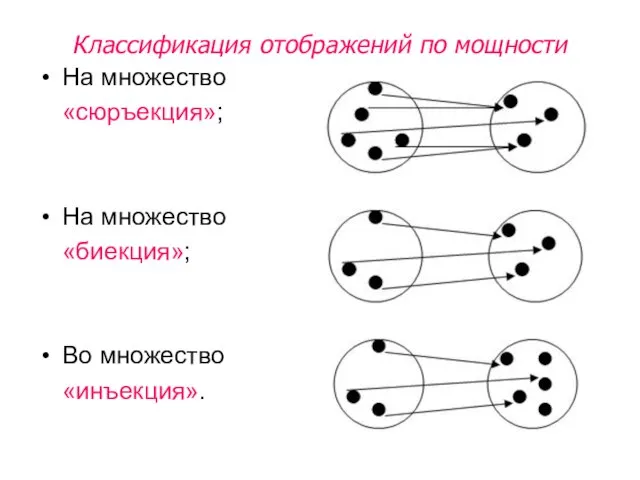
- 55. Классификация отображений по мощности На множество «сюръекция»; На множество «биекция»; Во множество «инъекция».
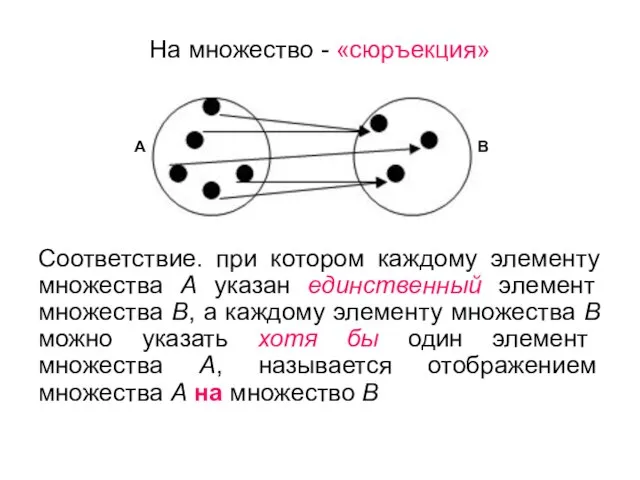
- 56. На множество - «сюръекция» Соответствие. при котором каждому элементу множества А указан единственный элемент множества В,
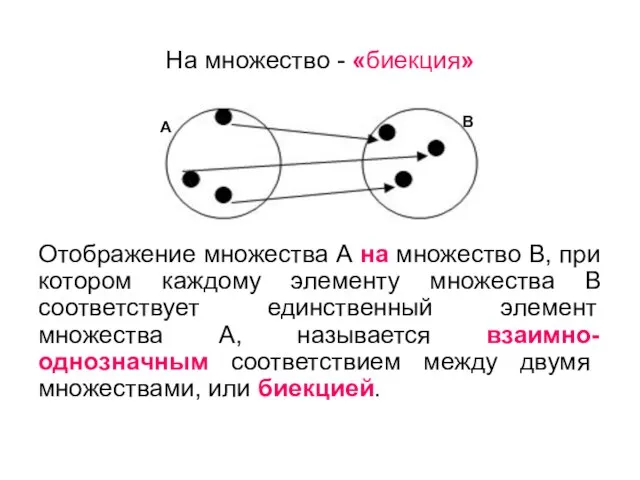
- 57. На множество - «биекция» Отображение множества А на множество В, при котором каждому элементу множества В
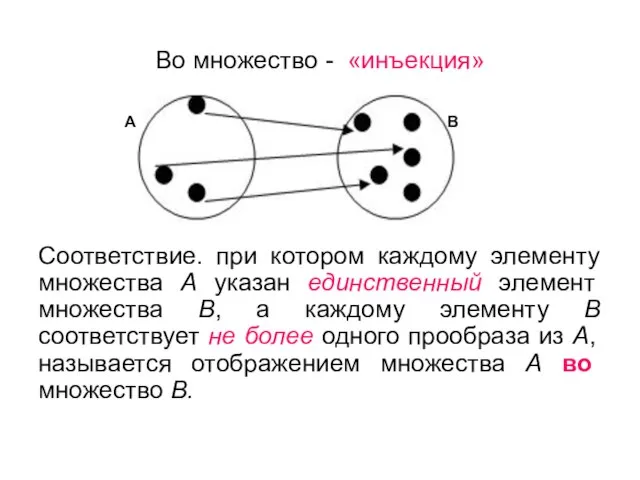
- 58. Во множество - «инъекция» Соответствие. при котором каждому элементу множества А указан единственный элемент множества В,
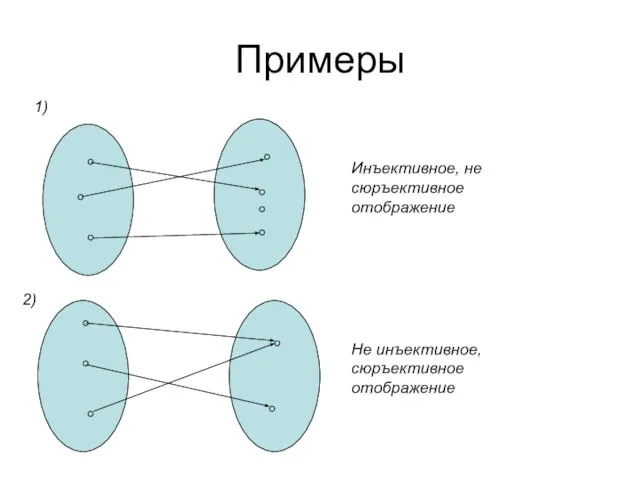
- 59. Примеры Инъективное, не сюръективное отображение Не инъективное, сюръективное отображение
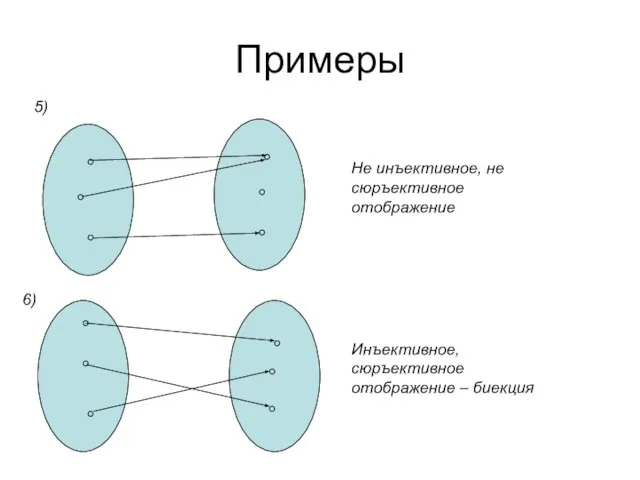
- 60. Примеры Не инъективное, не сюръективное отображение Инъективное, сюръективное отображение – биекция
- 61. Примеры 7) Список студентов – биекция между номером и фамилией. 8) , где - множество экзаменов
- 63. Скачать презентацию










































 Системы счисления
Системы счисления Первообразная. Таблица для нахождения первообразных элементарных функций
Первообразная. Таблица для нахождения первообразных элементарных функций Специальная теория относительности
Специальная теория относительности Линейная алгебра. Применение определителей
Линейная алгебра. Применение определителей Свойства степени
Свойства степени Тесты по математике
Тесты по математике Сложение вида +6
Сложение вида +6 Задание 19. Профиль (1)
Задание 19. Профиль (1)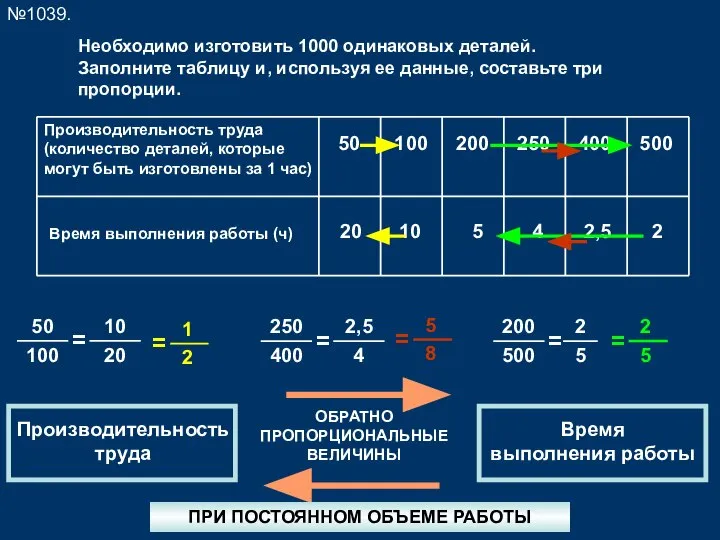 Пропорциональные величины
Пропорциональные величины Скалярное произведение векторов
Скалярное произведение векторов Случаи вычитания 12 -
Случаи вычитания 12 - Устный счёт. Транспорт
Устный счёт. Транспорт Как посчитать консонанс
Как посчитать консонанс Презентация на тему Нахождение неизвестного по двум разностям
Презентация на тему Нахождение неизвестного по двум разностям  Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников 1155274
1155274 Векторная алгебра
Векторная алгебра ерпендикулярность прямых и плоскостей. Теорема о трех перпендикулярах
ерпендикулярность прямых и плоскостей. Теорема о трех перпендикулярах Логика предикатов
Логика предикатов Возвратные уравнения
Возвратные уравнения Параллельность прямых
Параллельность прямых Формула Пика
Формула Пика Первообразная. Таблица первообразных
Первообразная. Таблица первообразных урок 1,2 по геометрии 11 класс 6 сентября 2022
урок 1,2 по геометрии 11 класс 6 сентября 2022 Решение экономических задач
Решение экономических задач Использование циклов
Использование циклов Устный счёт
Устный счёт Формулы для решения С2 координатно-векторным способом
Формулы для решения С2 координатно-векторным способом