Теоремы Чевы и Менелая

Теоремы Чевы и Менелая
«Обладая литературой более обширной, чем алгебра и арифметика вместе взятые, и по крайней мере столь же обширной, как анализ, геометрия в большей степени чем любой другой раздел математики, является богатейшей сокровищницей интереснейших, но полузабытых вещей, которыми спешащее поколение не имеет времени насладиться». Е. Т. Белл.

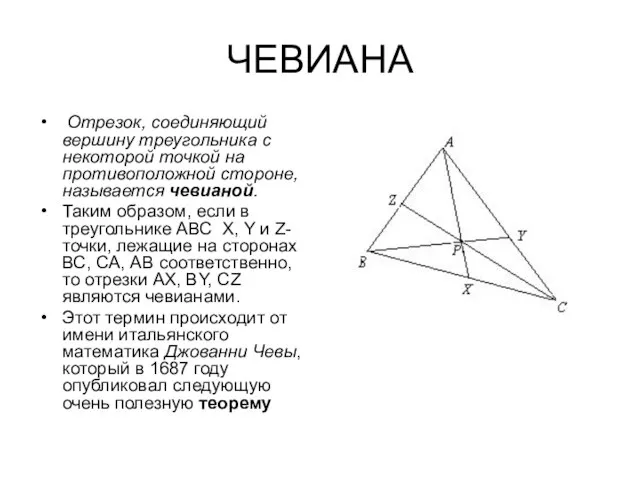
ЧЕВИАНА
Отрезок, соединяющий вершину треугольника с некоторой точкой на противоположной стороне, называется чевианой.
Таким образом, если в треугольнике АВС X, Y и Z- точки, лежащие на сторонах ВС, СА, АВ соответственно, то отрезки АX, ВY, СZ являются чевианами.
Этот термин происходит от имени итальянского математика Джованни Чевы, который в 1687 году опубликовал следующую очень полезную теорему

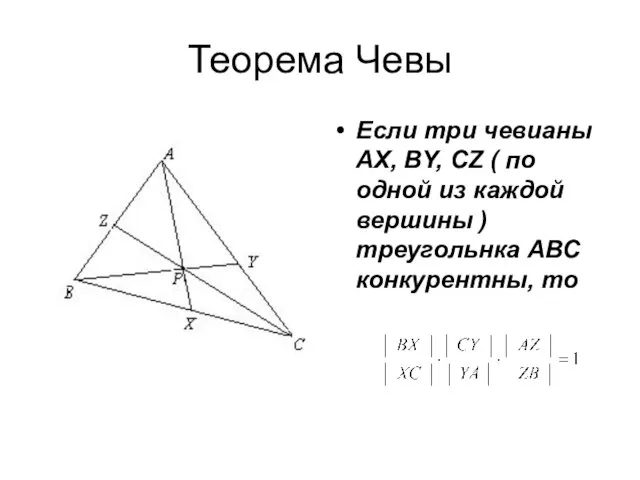
Теорема Чевы
Если три чевианы АX, ВY, СZ ( по одной из каждой вершины ) треугольнка АВС конкурентны, то

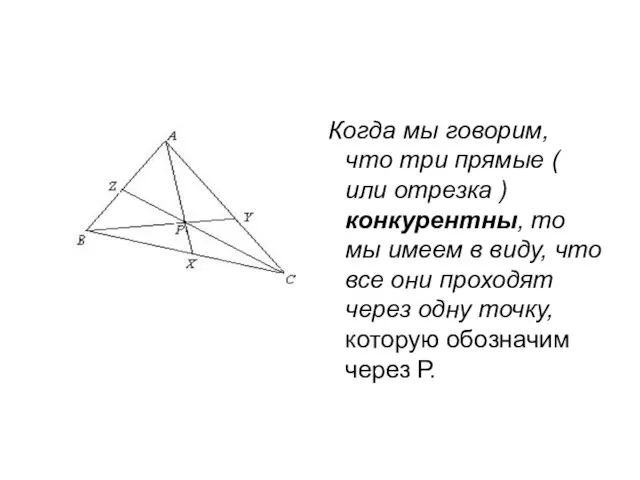
Когда мы говорим, что три прямые ( или отрезка ) конкурентны, то мы имеем в виду, что все они проходят через одну точку, которую обозначим через Р.

ДОКАЗАТЕЛЬСТВО
Для доказательства теоремы Чевы вспомним, что площади треугольников с равными высотами пропорциональны основаниям треугольников.
♦ Ссылаясь на рисунок, мы имеем

Теперь, если мы перемножим их, то получим
.

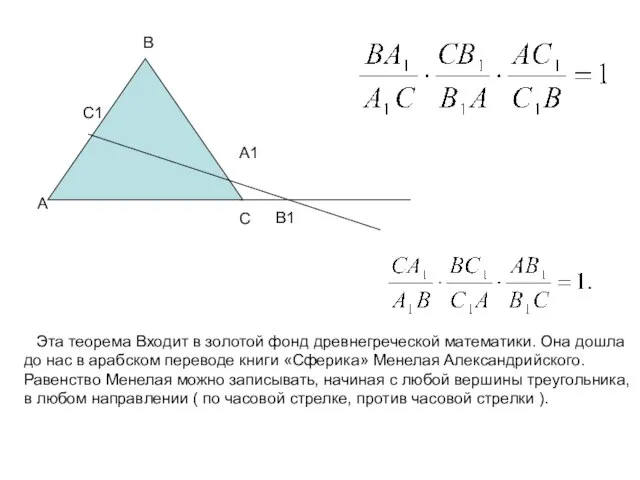
Теорема Менелая:
Пусть точка А1 лежит на стороне ВС треугольника АВС, точка С1 – на стороне АВ, точка В1 – на продолжении стороны АС за точку С. Точки А1,В1 иС1 лежат на одной прямой тогда и только тогда, когда выполняется равенство

А
В1
В
С
А1
С1
Эта теорема Входит в золотой фонд древнегреческой математики. Она дошла до нас в арабском переводе книги «Сферика» Менелая Александрийского. Равенство Менелая можно записывать, начиная с любой вершины треугольника, в любом направлении ( по часовой стрелке, против часовой стрелки ).

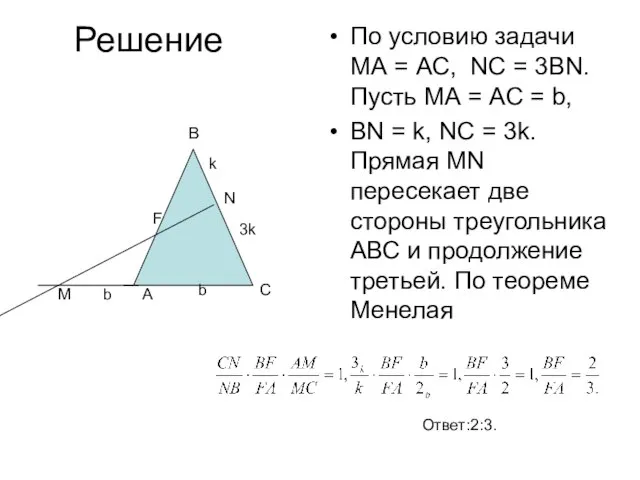
Задача 1.
В треугольнике АВС на стороне ВС взята точка N так, что NC = 3BN; на продолжении стороны АС за точку А взята точка М так, что МА=АС. Прямая MN пересекает сторону АВ в точке F. Найдите: отношение

Решение
По условию задачи МА = АС, NC = 3BN. Пусть МА = АС = b,
BN = k, NC = 3k. Прямая MN пересекает две стороны треугольника АВС и продолжение третьей. По теореме Менелая
В
F
C
А
M
N
k
3k
b
b
Ответ:2:3.