Булева алгебра

Основные определения
Все переменные логической функции и сама функция могут принимать только два значения: 0 и 1.

Основные определения
Логические функции могут быть заданы аналитически (в виде формулы), геометрически, словесно или с помощью таблиц истинности.
Различных функций n переменных

Булевы функции от одного аргумента
Логических функций одного аргумента всего

Булевы функции от одного аргумента

Булевы функции от двух аргументов
Булева функция от двух аргументов сопоставляет любой упорядоченной паре, составленной из элементов 0 и 1 (а таких упорядоченных пар будет четыре), либо 0, либо 1.
Логических функций двух аргументов всего

Булевы функции от двух аргументов

Для некоторых булевых функций двух переменных введены специальные обозначения.
Булевы функции от двух аргументов

Формулы, представляющие одну и ту же функцию называются эквивалентными или равносильными (обозначаются =).

Законы и теоремы булевой алгебры
Основные эквивалентные соотношения:
1. Ассоциативность & и V (сочетательный закон):
а) x1⋅(x2⋅x3)=(x1⋅x2)⋅x3=x1⋅x2⋅x3, б) x1+(x2+x3)=(x1+x2)+x3=x1+x2+x3.
2. Коммутативность & и V (переместительный закон):
а) x1⋅x2=x2⋅x1, б) x1+x2=x2+x1.
3. Дистрибутивность (распределительный закон):
а) x1⋅(x2+x3)=x1⋅x2+ x1⋅x3, б) x1+(x2⋅x3)=(x1+x2)⋅(x1+x3).
4. Идемпотентность (отсутствие степеней):
а) x⋅x=x, б) x+x=x.

5. Закон двойного отрицания: x = x.
6. Свойства констант 0 и 1:
а) x⋅1=x, б) x⋅0=0, в) x+1=1,
г) x+0=x, д) 0=1, е) 1=0.
7. Теорема двойственности (правила де Моргана):
а) x ⋅ y = x + y , б) x + y = x ⋅ y .
8. Закон противоречия: x⋅ х =0.
9. Закон исключённого третьего: x + x =1.
Законы и теоремы булевой алгебры

Часто используемые эквивалентные соотношения, выводимые из основных:
Поглощение: x+xy=x; x+xy=x+y
Склеивание: xy+xy=x; (x+y)(x+y)=x
Законы и теоремы булевой алгебры

Выражение бинарных логических функций через основные (&, V, ¬):
x→y = x+y
x~y =x⋅y+x⋅y
x⊕y = x⋅y+x⋅y
x’y = x⋅y = x+y
x↓y = x+y = x⋅y
Законы и теоремы булевой алгебры

x1+x2=x2+x1
x~y =x⋅y+x⋅y
x + x =1
x+xy=x; x+xy=x+y
x→y = x+y
x↓y = x+y = x⋅y
x’y = x⋅y = x+y
x1⋅(x2+x3)=x1⋅x2+ x1⋅x3
Диктант «Основные эквивалентные соотношения»

x ⋅ y = x + y , x + y = x ⋅ y
xy+xy=x; (x+y)(x+y)=x
x1⋅(x2⋅x3)=(x1⋅x2)⋅x3=x1⋅x2⋅x3
x⊕y = x⋅y+x⋅y
x⋅ х =0
а) x⋅1=x, б) x⋅0=0, в) x+1=1,
г) x+0=x, д) 0=1, е) 1=0.
x = x.
Диктант «Основные эквивалентные соотношения»

Критерии оценок:
14, 15 правильных ответов – «5»
11 – 13 правильных ответов – «4»
8 – 10 правильных ответов – «3»
< 8 правильных ответов – «2»
Диктант «Основные эквивалентные соотношения»

Диктант «Основные эквивалентные соотношения» - 2
x1⋅(x2+x3)=x1⋅x2+ x1⋅x3
x1+x2=x2+x1
x ⋅ y = x + y , x + y = x ⋅ y
x~y =x⋅y+x⋅y
xy+xy=x; (x+y)(x+y)=x
x + x =1
x1⋅(x2⋅x3)=(x1⋅x2)⋅x3=x1⋅x2⋅x3
x+xy=x; x+xy=x+y

x⊕y = x⋅y+x⋅y
x→y = x+y
x⋅ х =0
x↓y = x+y = x⋅y
а) x⋅1=x, б) x⋅0=0, в) x+1=1,
г) x+0=x, д) 0=1, е) 1=0.
x’y = x⋅y = x+y
x = x.
Диктант «Основные эквивалентные соотношения» - 2

Критерии оценок:
14, 15 правильных ответов – «5»
11 – 13 правильных ответов – «4»
8 – 10 правильных ответов – «3»
< 8 правильных ответов – «2»
Диктант «Основные эквивалентные соотношения»

Самостоятельная работа
Вариант 1
Дать определение &, ~, ¬, ↓
Выяснить, являются ли формулы равносильными: (y+(x→z))+x+z и x+y+z
Доказать, что формула является тавтологией: ((a+b)→(a⋅c))+b
Вариант 2
Дать определение V, ⊕, →, ′
Выяснить, являются ли формулы равносильными: (x~y)+y+z и y⋅(x+z)+x⋅ y
Доказать, что формула является тавтологией: (b+(a→c))+(a+c)+b

Нормальные формы булевых функций

ДНФ
Элементарной конъюнкцией называется конъюнкция одной или нескольких переменных, при этом каждая переменная встречается не более одного раза (либо сама, либо ее отрицание).
Примеры элементарных конъюнкций:
Примеры неэлементарных конъюнкций:

ДНФ
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция конечного числа элементарных конъюнкций.
Пример ДНФ:
Пример: привести функцию ((x↓y)+(x~z)) к ДНФ.
Решение: ((x↓y)+(x~z)) = x⋅y+xz+xz

СДНФ
Нормальная дизъюнктивная форма называется совершенной (СДНФ), если в каждой ее элементарной конъюнкции представлены все переменные, входящие в данную функцию (либо сами, либо с отрицаниями).
Пример СДНФ:

Построение СДНФ по ТИ
Пусть функция f(x1, x2, …,xn) задана своей таблицей истинности (ТИ).
Подчеркнуть наборы переменных, на которых функция равна 1;
Составить из переменных полные конъюнкции, причем, если переменная входит в набор с 0, то нужно взять ее отрицание.
Соединить конъюнкции знаком дизъюнкции.

КНФ
Элементарной дизъюнкцией называется дизъюнкция одной или нескольких переменных, при этом каждая переменная встречается не более одного раза (либо сама, либо ее отрицание).
Конъюнктивной нормальной формой (КНФ) называется конъюнкция конечного числа элементарных дизъюнкций.
Пример КНФ:

СКНФ
Нормальная конъюнктивная форма называется совершенной (СКНФ), если в каждой ее элементарной дизъюнкции представлены все переменные, входящие в данную функцию (либо сами, либо с отрицаниями).
Пример СКНФ:

Приведение ДНФ к КНФ
Пусть ДНФ имеет вид F=k1+ k2+ k3+…+ kn, где ki – эл. конъюнкции.
Применить к ДНФ правило двойного отрицания
F = F= k1+ k2+ k3+…+ km
и привести k1+ k2+ k3+…+ km к ДНФ:
где - элементарные конъюнкции.
С помощью правил де Моргана освободиться от второго отрицания и преобразовать отрицания элементарных конъюнкций в элементарные дизъюнкции d1, d2, …, dp, т.е.

Построение СКНФ по ТИ
Пусть функция f(x1, x2, …,xn) задана своей таблицей истинности (ТИ).
Подчеркнуть наборы переменных, на которых функция равна 0;
Составить из переменных полные дизъюнкции, причем, если переменная входит в набор с 1, то нужно взять ее отрицание.
Соединить дизъюнкции знаком конъюнкции.

Построение СКНФ по ТИ
Пример: Построить СКНФ для функции, заданной своей таблицей истинности:

Пример: Построить СДНФ и СКНФ для функции f(x1,x2,x3).
Построение СКНФ по ТИ

Карты Карно
Карты Карно – один из наиболее удобных способов минимизации логических функций. Впервые появились в статье Мориса Карно в 1953 г.
Это специальные таблицы, дающие возможность упростить процесс поиска формы булевой функции с помощью графического представления для n≤6 (n – количество переменных в функции).

Карта Карно – это таблица из 2n клеток, в каждой из которых проставляется значение функции, соответствующее каждому набору переменных.
n=2
Карты Карно
x1 x1
x2
x2
Пример.
x1 x1
x2
x2
СДНФ: f(x1,x2)=x1x2+ x1x2

n = 3
Карты Карно
x1x2 x1x2 x1x2 x1x2
x3
x3
f(x,y.z)= xyz+xyz+ xyz+xyz
xy xy xy xy
z
z
Пример:
1
1
1
1
0
0
0
0

n = 4
Карты Карно
x1x2 x1x2 x1x2 x1x2
x3x4
x3x4
x3x4
x3x4
Пример: f(a,b,c,d) = abcd + abcd + abcd + abcd + abcd
ab ab ab ab
cd
cd
cd
cd
1
1
1
1
1

Карты Карно
xy xy xy xy
z
z
Пример. Составить карту Карно для функции трех переменных:
f(x,y.z) =

zt
zt
zt
zt
Карты Карно
Пример. Составить карту Карно для функции четырех переменных:
xy xy xy xy
f(x,y.z,t)=

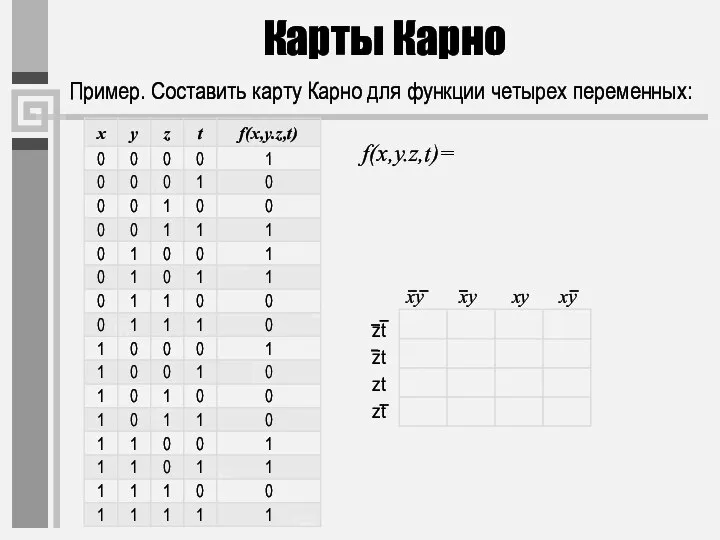
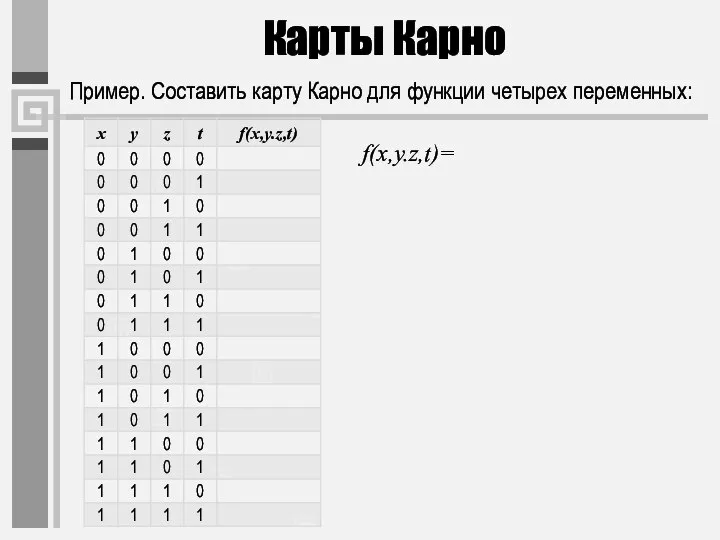
Карты Карно
Пример. Составить карту Карно для функции четырех переменных:
f(x,y.z,t)=

Для построения минимальной ДНФ производится «склеивание» единиц. Склеиваются только соседние клетки, которые отличаются значением одной переменной. Процесс сводится к объединению в группы единичных клеток карт Карно. При этом одинаковые переменные сохраняются, а различные опускаются.
Карты Карно

Алгоритм минимизации б/ф с помощью карт Карно
Привести б/ф к ДНФ;
Нанести единицы на карту Карно;
Объединить соседние единицы контурами, охватывающими 1, 2, 4, 8 клеток (виде квадрата или прямоугольника);
Провести упрощение, т.е. описать каждую группу одной элементарной конъюнкцией, в которую входят только неизменные для всех ячеек данной группы переменные;
Объединить полученные элементарные конъюнкции знаками дизъюнкции.
Карты Карно

Карты Карно
xy xy xy xy
z
z
Пример. Минимизировать б/ф трех переменных с помощью карт Карно.
f(x,y.z) =

zt
zt
zt
zt
Карты Карно
Пример. Минимизировать б/ф четырех переменных с помощью к. К.
xy xy xy xy
f(x,y.z,t)=

Карты Карно
Пример. Минимизировать б/ф четырех переменных с помощью карт Карно.
f(a,b,c,d)=abcd+ abcd+ abcd+ abcd+ abcd+ abcd+ abcd.
ab
ab
ab
ab
Решение:
f(a,b,c,d)=

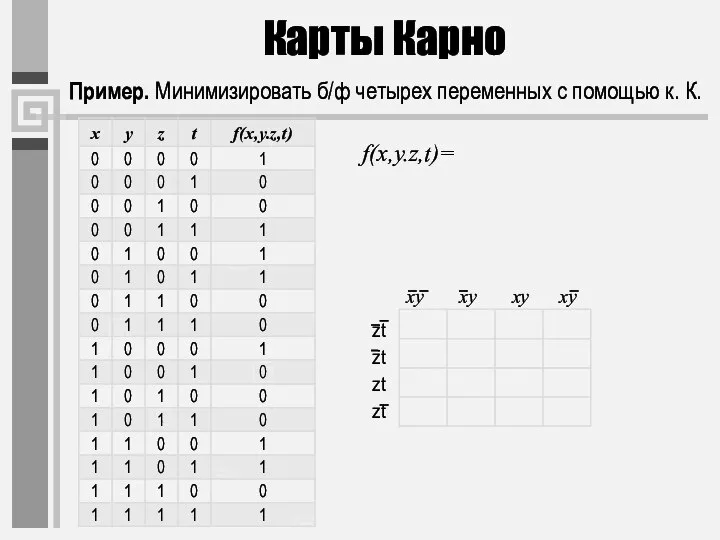
Пример. Минимизировать б/ф
f(x,y,z,t)= xyzt+ xyzt+ xyzt+ xyzt+ xyzt + xyzt.
f(x,y,z,t)=
Карты Карно
zt
zt
zt
zt
xy xy xy xy
Решение:

Пример. Минимизировать б/ф
f(x,y,z,t)= xyzt+ xyzt+ xyzt+ xyzt.
f(x,y,z,t)=
Карты Карно
Решение:
zt zt zt zt

ПОЛИНОМ ЖЕГАЛКИНА

Выражение бинарных логических функций через основные (&, V, ¬):
x→y = x+y
x~y =x⋅y+x⋅y
x⊕y = x⋅y+x⋅y
x’y = x⋅y = x+y
x↓y = x+y = x⋅y
Законы и теоремы булевой алгебры

Полином Жегалкина
Определение. Полиномом Жегалкина (полиномом по модулю 2) от n переменных x1,x2 ... xn называется выражение вида:
P(x1x2 ... xn) = C0⊕C1x1⊕C2x2⊕ ... ⊕Cnxn⊕C12x1x2⊕ ... ⊕C12 ... nx1x2 ... xn
где постоянные Ck могут принимать значения 0 ли 1.
Пример. P=1⊕x2⊕x1x3⊕x1x2 x4– полином Жегалкина.

Общий вид мн-на Жегалкина для функций двух и трех переменных
Для функции двух переменных многочлен Жегалкина имеет вид:
P(x1,x2) = C0⊕C1x1⊕C2x2⊕C12x1x2
Для функции трех переменных многочлен Жегалкина имеет вид:
P(x1,x2,x3) = C0⊕C1x1⊕C2x2⊕C3x3⊕C12x1x2⊕C13x1x3 ⊕C23x2x3⊕C123x1x2x3
Пример. P=1⊕x2⊕x1x3⊕x1x2 x3

Линейная функция
Если полином Жегалкина не содержит произведений отдельных переменных, то он называется линейным (линейная функция).
Пример:
f=x⊕yz⊕xyz
f=1⊕x⊕y⊕z - линейная функция.
Теорема. Каждая булева функция представляется в виде полинома Жегалкина единственным образом.

Основные свойства ⊕ и &
1. коммутативность
x⊕y=y⊕x x&y=y&x
2. ассоциативность
x⊕(y⊕z)=(x⊕y)⊕z
x&(y&z)=(x&y)&z
3. дистрибутивность
x&(y⊕z)=(x&z)⊕(x&z)
4.

Выражение дизъюнкции через ⊕
Докажем, что x+y=x⊕y⊕xy
Решение:
учитывая, используя формулы
де Моргана и соотношения
выразим

Полиномы Жегалкина элементарных булевых функций
x+y=x⊕y⊕xy
x∼y=1⊕x⊕y
x→y=1⊕x⊕xy
x↓y=1⊕x⊕y⊕xy
x|y=1⊕xy

Методы построения полиномов Жегалкина
Метод неопределенных коэффициентов (по ТИ)
Метод преобразования формул из СДНФ
Метод преобразования формул из ДНФ

Метод неопределенных коэффициентов
Пример. Построить полином Жегалкина функции f(x,y)=x→y
Решение.
Запишем искомый полином в виде:
P=C0⊕C1x⊕C2y⊕C12xy
Пользуясь таблицей истинности
получаем, что
f(0,0)=P(0,0)=C0=1
f(0,1)=P(0,1)=C0⊕C2=1
f(1,0)=P(1,0)=C0⊕C1=0
f(1,1)=P(1,1)=C0⊕C1⊕C2⊕C12=1
Откуда последовательно находим, C0=1, C1=1, C2=0, C12=1
Следовательно: x→y=1⊕x⊕xy.

Для функции двух переменных
P(0,0)=C0
P(0,1)=C0⊕C2
P(1,0)=C0⊕C1
P(1,1)=C0⊕C1⊕C2⊕C12
Метод неопределенных коэффициентов

Для функции трех переменных
P(0,0,0)= C0
P(0,0,1)= C0⊕C3
P(0,1,0)= C0⊕C2
P(0,1,1)= C0⊕C2⊕C3⊕C23
P(1,0,0)= C0⊕C1
P(1,0,1)= C0⊕C1⊕C3⊕C13
P(1,1,0)= C0⊕C1⊕C2⊕C12
P(1,1,1)= C0⊕C1⊕C2⊕C3⊕C12⊕C13 ⊕C23⊕C123
Метод неопределенных коэффициентов

Метод преобразования формул из СДНФ
Пусть задана СДНФ функции f(x1, …, xn).
Заменяем каждый символ дизъюнкции на символ дизъюнкции с исключением.
Заменяем каждую переменную x = x ⊕1.
Раскрываем скобки.
Вычеркиваем из формулы пары одинаковых слагаемых.
Получен полином Жегалкина функции f(x1, …, xn).

Пример
Метод преобразования формул из СДНФ

Метод преобразования формул из ДНФ
Пусть задана произвольная ДНФ функции f(x1, …, xn).
Разбиваем ДНФ на пары конъюнкций (если число конъюнкций нечетно, одна из них остается без пары).
Заменяем дизъюнкцию каждой пары конъюнкций K1+ K2 =K1⊕K2⊕K1K2
В полученной формуле находим очередную дизъюнкцию A1+A2 и заменяем ее формулой A1⊕ A2⊕A1A2. Повторяем шаг 3 до тех пор, пока это возможно.
Заменяем каждую переменную с инверсией x =x ⊕ 1.
Раскрываем скобки.
Вычеркиваем из формулы пары одинаковых слагаемых.
Получен полином Жегалкина функции f(x1, …, xn).

Пример
Метод преобразования формул из ДНФ