Стереометрия. Школьный курс

Существует
принадлежит
Пересечение/
пересекаются
Не принадлежит
Перпендикулярность/
перпендикулярны
Параллельность/параллельны
Так обозначаются плоскости
Так обозначаются прямые
Обозначения

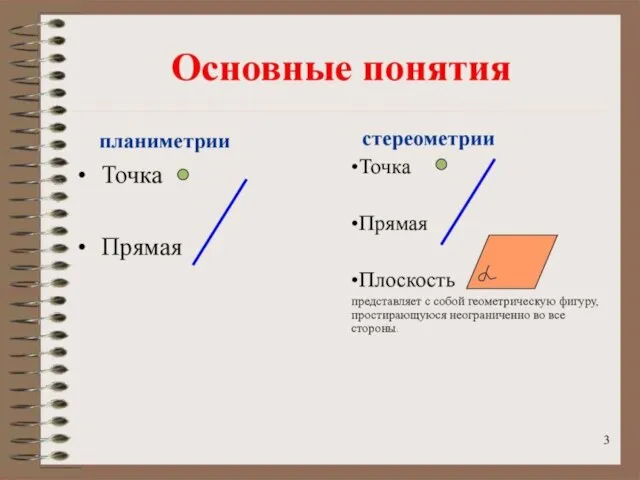
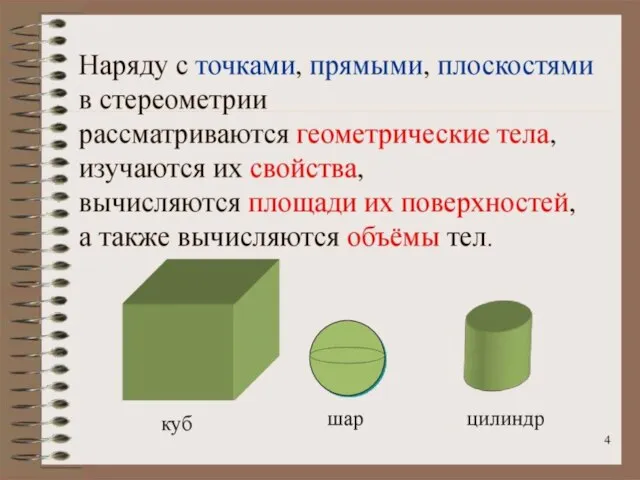
Аксиомы стереометрии
Аксиома 1.
Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и не принадлежащие ей.

Аксиома 2.
Если две различные плоскости имеют общую точку, то они пересекаются по прямой.

Аксиома 3.
Через две пересекающиеся прямые можно провести плоскость и притом только одну.

Следствие 1.
Через прямую и не лежащую на ней точку проходит плоскость и притом только одна.

Следствие 2.
Если две точки прямой лежат в плоскости, то вся прямая лежит в этой плоскости.

Следствие 3.
Через три точки, не лежащие на одной прямой, проходит плоскость и притом только одна.

a
…
ПАРАЛЛЕЛЬНОСТЬ

ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ
ПАРАЛЛЕЛЬНОСТЬ
ПРЯМОЙ И ПЛОСКОСТИ
ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ

ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ
Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.
Две прямые называются скрещивающимися, если они лежат в разных плоскостях и не пересекаются.

ТЕОРЕМА 1.
ЧЕРЕЗ ТОЧКУ, НЕ ЛЕЖАЩУЮ НА ПРЯМОЙ,
В ПРОСТРАНСТВЕ МОЖНО ПРОВЕСТИ ПАРАЛЛЕЛЬНУЮ ПРЯМУЮ И ПРИТОМ ТОЛЬКО ОДНУ.
а
А
Дано:
Доказать:
Доказательство:
проходящая через А, || a и
притом единственная
Проведем через a и A плоскость α.
В плоскости α проведем прямую a1 , || a.
Докажем, что a1 - единственная.
Метод от противного.
Пусть существует a2||a.
Проведем через a и a2 плоскость α2.
Плоскость α2 проходит через a и A .
По следствию 1 плоскость α2 совпадает с α.
Значит, прямая единственная, что и т.д.

ТЕОРЕМА 2.
ДВЕ ПРЯМЫЕ, ПАРАЛЛЕЛЬНЫЕ ТРЕТЬЕЙ ПРЯМОЙ, ПАРАЛЛЕЛЬНЫ.
Без доказательства

ПАРАЛЛЕЛЬНОСТЬ
ПРЯМОЙ И ПЛОСКОСТИ
Прямая и плоскость называются параллельными, если они не пересекаются.

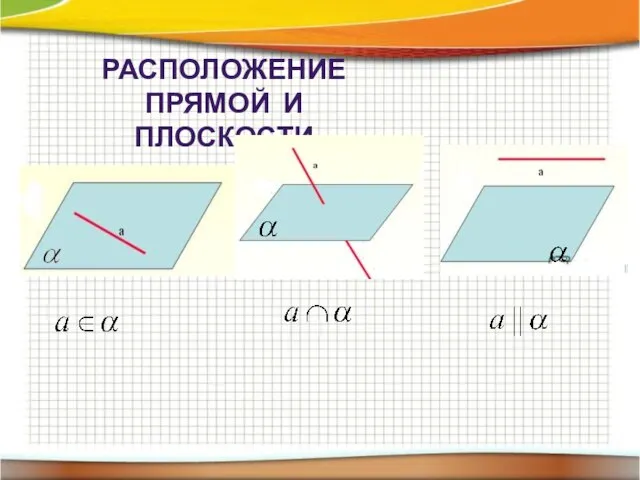
РАСПОЛОЖЕНИЕ
ПРЯМОЙ И ПЛОСКОСТИ

ТЕОРЕМА 3.
ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ.
ЕСЛИ ПРЯМАЯ, НЕ ПРИНАДЛЕЖАЩАЯ ПЛОСКОСТИ, ПАРАЛЛЕЛЬНА КАКОЙ-НИБУДЬ ПРЯМОЙ, ЛЕЖАЩЕЙ В ПЛОСКОСТИ, ТО ОНА ПАРАЛЛЕЛЬНА И САМОЙ ПЛОСКОСТИ.
Дано:
Доказать:
Доказательство:
Проведем через a и a1 плоскость α2 .
Плоскости α2 и α пересекаются по прямой a1 .
Метод от противного.
Пусть a пересекает α. Тогда бы a пересекала a1 .
Это противоречит условию
Значит предположение не верно, то есть,
что и т.д.

ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ
Две плоскости называются параллельными, если они не пересекаются.

ТЕОРЕМА 4.
ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПЛОСКОСТЕЙ.
ДВЕ ПЛОСКОСТИ ПАРАЛЛЕЛЬНЫ, ЕСЛИ ОДНА ИЗ НИХ ПАРАЛЛЕЛЬНА ДВУМ ПЕРЕСЕКАЮЩИМСЯ ПРЯМЫМ, ЛЕЖАЩИМ В ДРУГОЙ ПЛОСКОСТИ.
Дано:
Доказать:
Доказательство:
Метод от противного.
Пусть плоскости пересекает по прямой с.
Т.к. значит не пересекаются с прямой с.
Но . Возникло противоречие.
Предположение неверно, плоскости параллельны, что и т.д.

ТЕОРЕМА 5.
ЧЕРЕЗ ТОЧКУ, НЕ ЛЕЖАЩУЮ В ПЛОСКОСТИ, МОЖНО ПРОВЕСТИ ПАРАЛЛЕЛЬНУЮ ПЛОСКОСТЬ И ПРИТОМ ТОЛЬКО ОДНУ.
Без доказательства

СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ
1. Если две параллельные плоскости пересечены третьей, то прямые пересечения параллельны.