Проектирование последовательностных схем

Основные определения и обозначения
Блок-схема последовательностного устройства
х1х2х3 – входные величины
f1f2f3 – выходные величины
Y1Y2Y3 – возбуждаемые значения вторичных переменных
y1y2y3 –значения вторичных переменных определяющие устойчивое состояние схемы
Способность последовательностных схем сохранять память о прошлых событиях описывается так называемыми вторичными переменными, отображающими процесс установления в схеме определенного состояния.
Одно или несколько последовательных состояний характеризуют режим работы схемы.
Вторичным переменным присуще запаздывание между их возбуждаемыми (Y) и последующими установившимися (y) значениями, соответствующими новому (изменившемуся) состоянию схемы.

Понятие устойчивости
При проектировании последовательностных схем используется описание условий перехода схем из одного состояния в другое. Смена состояний связана с изменением значения хотя бы одной вторичной переменной.
Состояние схемы неустойчиво, если значение переменной претерпевает изменение.
Состояние устойчиво при отсутствии таких изменений.
Когда возбуждаемое значение вторичной переменной совпадает с ее установившимся значением (Y = y), эта переменная не претерпевает изменений и называется устойчивой (на данном шаге).
Если возбуждаемое и установившееся значения переменной не совпадают (Y ≠ у), переменная неустойчива, и должна произойти смена состояний.
При у=0 и Y=0 (у=1 и Y=1 ) смена состояния не требуется, и вторичная переменная устойчива.
При у=0 и Y=1 (у=1 и Y=0), смена состояния необходима, и вторичная переменная неустойчива.

Функционирование последовательностной схемы
Значения функции на выходе (f) и возбуждаемые значения вторичных переменных (Y) зависят от значений входных переменных (x) и вторичных переменных (y), определяющих состояния схемы.
Таким образом, вторичные переменные используются при выработке их собственных новых значений.
В процессе перехода схемы из одного состояния в другое можно выделить последовательные этапы.
Смену состояний схемы вызывают входные переменные (x).
Изменение значений входных переменных приводит к изменению возбуждаемых вторичных переменных (Y).
После короткой задержки во времени это вызывает изменение значений вторичных переменных (y) на входе комбинационной части схемы.
Если состояние схемы становится устойчивым, то дальнейших изменений не происходит.
Если же новое состояние неустойчиво, еще раз изменяются значения возбуждаемых вторичных переменных (Y), а затем и их значения на входе комбинационной части схемы. Изменения подобного рода продолжаются, пока система не перейдет в устойчивое состояние. Поскольку значения функции на выходе последовательностной схемы (f) зависят от значений входных (x) и вторичных переменных (y), эту функцию можно рассматривать как устойчивую вторичную переменную.

Построение графа переходов
При проектировании последовательностных схем первым шагом является построение графа перехода из одного состояния в другое на основании словесного описания работы схемы.
Первоначально задав любой возможный набор значений входных переменных, с помощью линий со стрелками изображают переход из состояния в состояние для каждого изменения значения входной переменной.
Поскольку по условию допускаются изменения лишь какой-либо одной переменной, число стрелок, исходящих из состояния, может равняться числу переменных. Однако из постановки задачи обычно вытекают ограничения на это число (оно может оказываться равным единице) .
Построение графа переходов продолжается аналогичным образом, пока все намеченные стрелками направления не превратятся в замкнутые линии.
Граф переходов
Одномоментно может меняться только один входной аргумент
(1), (2), …, (6) – устойчивые состояния схемы

Таблица переходов переходов
Второй шаг проектирования заключается в построении таблицы переходов. Эта таблица используется как средство преобразования графа переходов в карту с целью формирования логических выражений для возбуждаемых вторичных переменных и выходных функций.
По внешнему виду таблица переходов напоминает карту. Однако, подобно графу переходов, в таблице имеется свой строгий порядок расположения элементов.
Все события в схемах порождаются изменениями значений входных переменных (х1х2).
В таблице переходов каждой комбинации значений входных переменных соответствует определенный столбец.
Смена значений входных переменных означает смену столбца в таблице.
Для каждого возможного сочетания значений х1х2 выделен отдельный столбец и каждому возможному состоянию схемы соответствует цифра на пересечении столбца и строки таблицы переходов.
Устойчивые состояния выделены кружками, а неустойчивые не выделяются.

Исключение избыточных устойчивых состояний
При построении графа переходов в рассмотрение может оказаться включенным больше состояний, чем на самом деле необходимо.
Если два состояния эквивалентны, то одно из них является избыточным и должно быть исключено. В ряде случаев наличие избыточных состояний не является очевидным фактом. Однако избыточность может быть легко обнаружена при анализе таблиц переходов. Выявление избыточных состояний является следующим шагом в проектировании схемы.
Устойчивые состояния, отображенные в таблице переходов, являются избыточными, если
им соответствуют одни и те же значения входных сигналов (т. е. они появляются в одном и том же столбце таблицы);
им соответствуют одинаковые значения функций на выходе;
при любых допустимых изменениях входных сигналов переход, из этих состояний происходит в одинаковые или эквивалентные состояния.
Таблица переходов с эквивалентными состояниями (2) и (4).
а—исходная избыточная форма; б — после удаления четвертой строки.
а) б)

Процедура слияния строк
Слияние приводит к уменьшению числа вторичных переменных, необходимых для описания всех переходов, и, следовательно, для реализации соответствующей последовательностной схемы.
Слияние строк выполняют по следующим правилам:
1. Две или большее число строк могут быть слиты в одну, если элементы в идентичных позициях этих строк не противоречат друг другу, т. е. либо в идентичных позициях имеет место совпадение состояний, либо в соответствующей позиции одной «з строк может быть указано любое состояние.
2. Все номера состояний из объединяемых строк переписываются в соответствующие позиции результирующей строки. Если некоторое состояние отмечено кружком как устойчивое в одной из объединяемых строк, оно аналогичным образом отмечается и в объединенной строке. При операции слияния значения функций на выходе не принимаются во внимание и не указываются в таблице, строки которой подверглись процедуре слияния.

Построение диаграммы слияний начинают с последовательного расположения номеров строк по некоторой окружности.
Цифры на этой диаграмме указывают строки исходной таблицы переходов. Возможность слияния отдельных строк отмечают линиями между соответствующими номерами.
При построении диаграммы каждая строка должна быть сопоставлена со всеми другими строками для выявления возможности их слияния.
Анализ проведенных линий на диаграмме позволяет обнаружить наилучшую схему слияния.
Лучшими считают слияния, минимизирующие число строк результирующей таблицы.

Присвоение значений вторичным переменным
На следующем шаге проектирования каждой строке таблицы переходов, прошедшей процедуру слияния строк, ставится в соответствие комбинация значений вторичных переменных. Это необходимо для последующего построения карты возбуждений вторичных переменных (Y).
Присвоение значений вторичным переменным осуществляется, согласно карте переходов, по форме, похожей на карту Карно, без указания в клетках значений функции на выходе. Вместо них в клетки записываются буквенные обозначения столбцов таблицы переходов, претерпевшей слияния строк. Введение этих обозначений и выполняется на данном шаге проектирования.
Определению подлежат все возможные переходы между строками таблицы. Переход между двумя строками возможен, если они отличаются значением лишь одной переменной. Переход из неустойчивого состояния в требуемое устойчивое состояние возможен и через другую строку при условии, что не придется проходить через иное (неприемлемое) состояние.
Таблица переходов с указанием значений вторичных переменных.

Карта возбуждений
Условием наступления устойчивого состояния является совпадение возбуждаемых значений вторичных переменных с их установившимися значениями, указанными в соответствующей строке таблицы (Y=у).
Таблица возбуждений для устойчивых состояний
Содержимое клеток (Y1Y2) определяется следующим образом.
Устойчивым состояниям (1) и (2) соответствуют установившиеся значения вторичных переменных y1y2 = 00, а поэтому Y1Y2=00;
устойчивым состояниям (4) и (5) соответствует y1y2 = 11 и как следствие Y1Y2 = 11;
устойчивым состояниям (3) и (6) соответствует y1y2 = 10 и в результате Y1Y2 = 10.

Таблица возбуждений
На рисунке приведена построенная в соответствии с этим правилом карта возбуждений, элементы клеток которой (Y1Y2) определяются следующими логическими выражениями:
В клетках, соответствующих неустойчивым состояниям, должны указываться такие же значения Y1Y2, как и в клетках идентичных устойчивых состояний, в которые переходят неустойчивые состояния. Таким образом, все клетки с одинаковыми идентификаторами состояний содержат одинаковые значения Y1Y2.
Например, поскольку для устойчивого состояния (6) − Y1Y2 = 10, то и для состояния 6 − Y1Y2 = 10.
Незаполненные клетки карты возбуждений следует интерпретировать как клетки безразличия.

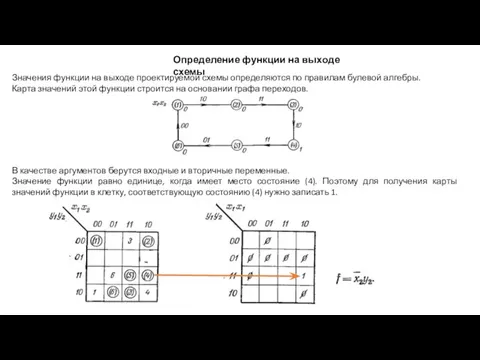
Определение функции на выходе схемы
Значения функции на выходе проектируемой схемы определяются по правилам булевой алгебры.
Карта значений этой функции строится на основании графа переходов.
В качестве аргументов берутся входные и вторичные переменные.
Значение функции равно единице, когда имеет место состояние (4). Поэтому для получения карты значений функции в клетку, соответствующую состоянию (4) нужно записать 1.

Построение схемы
На основании полученных логических выражений для карт возбуждений и выходной функции
выполняется заключительный шаг проектирования — формирование логической схемы на вентилях И-НЕ
Принципиальная электрическая схема
В соответствии с формулой
связи х1 и у1 к вентилю 307 являются избыточными
х
х