математической логики. Из его открытий наибольшую известность получил так называемый полином Жегалкина. Жегалкин награжден Орденом Трудового Красного Знамени. В своем письме М. Я. Выгодскому известный советский математик Николай Лузин, вспоминая студенческие годы, говорит, что из профессоров не боялся лишь Жегалкина.
Чарльз Сандерс Пирс (1839-1914)- американский философ, логик, математик, основоположник прагматизма и семиотики.
Ввёл в философию термин фанерон, предложил концепцию тихизма. В логику — стрелку Пирса, в картографию — проекцию Пирса. Немецкий философ Апель назвал Пирса «Кантом американской философии».















 Таблица умножения в пределах 100. Урок повторения и закрепления
Таблица умножения в пределах 100. Урок повторения и закрепления Методы доказательства теорем: прямой метод и метод от противного
Методы доказательства теорем: прямой метод и метод от противного Обучающие слайды
Обучающие слайды Геометрический смысл производной. Уравнение касательной
Геометрический смысл производной. Уравнение касательной Параллелограмм и трапеция. Урок 3
Параллелограмм и трапеция. Урок 3 Геометрические тела. Построение плоских срезов на геометрических телах
Геометрические тела. Построение плоских срезов на геометрических телах Решение задач с пропорциональными величинами
Решение задач с пропорциональными величинами Производная
Производная Интерполяционный многочлен Лагранжа
Интерполяционный многочлен Лагранжа Презентация по математике "Ломаные числа" -
Презентация по математике "Ломаные числа" -  Презентация на тему Перпендикуляр и наклонная
Презентация на тему Перпендикуляр и наклонная  Математика, Устный счёт
Математика, Устный счёт Число и цифра 3
Число и цифра 3 Теорема косинусов
Теорема косинусов Матрицы
Матрицы Делители числа
Делители числа Тайны треугольника. 7 класс
Тайны треугольника. 7 класс Корреляционный анализ
Корреляционный анализ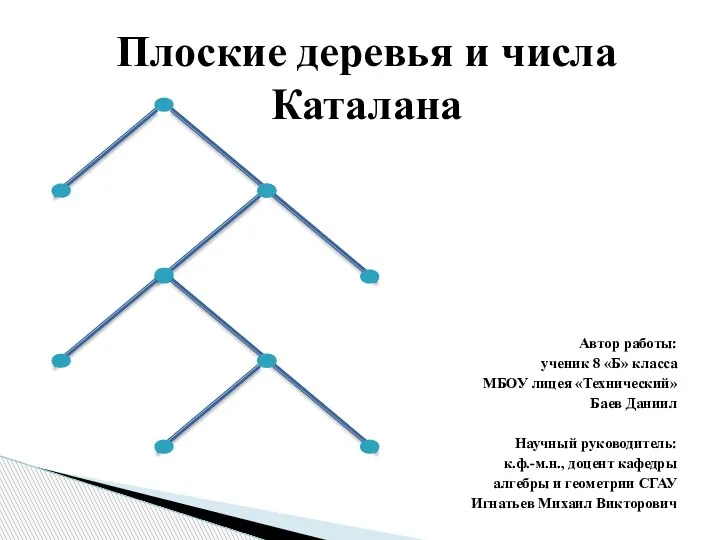 Плоские деревья и числа Каталана
Плоские деревья и числа Каталана Статистическая сводка и группировка
Статистическая сводка и группировка Конструктор (2)
Конструктор (2) Урок математики в 1 классе
Урок математики в 1 классе Трансформация объема бытового предмета геометрическими телами
Трансформация объема бытового предмета геометрическими телами Математическая карусель
Математическая карусель Формулы сокращенного умножения
Формулы сокращенного умножения Подготовка к контрольной работе
Подготовка к контрольной работе Реши самостоятельно
Реши самостоятельно Решение задач с применением раскрасок
Решение задач с применением раскрасок