Содержание
- 2. Дисперсия – одна из наиболее часто применяемых характеристик случайной величины. Может определяться для дискретной случайной величины
- 3. ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
- 4. ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Вся информация о случайной величине заложена в законе распределения, а математическое ожидание
- 5. ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Как можно было бы описать разброс значений случайной величины? Можно ввести отклонение
- 6. ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Чтобы получить не нулевое среднее отклонение можно говорить о модуле отклонения или
- 7. ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Дисперсией дискретной случайной величины X называется величина Величина X — случайная, а
- 8. ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Для закона распределения случайной величины дисперсию можно записать так
- 9. ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Дисперсия – одна из наиболее часто применяемых характеристик случайной величины. Она характеризует
- 10. ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Дисперсия всегда неотрицательна, это видно из определения дисперсии: в сумме присутствуют только
- 11. ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Дисперсия неслучайной величины равна нулю, что следует из определения дисперсии и свойства
- 12. ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Дисперсия от случайной величины умноженной на константу равна дисперсии случайной величины умноженной
- 13. ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Дисперсия суммы или разности двух независимых случайных величин равна сумме их дисперсий
- 14. ДИСПЕРСИЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
- 15. ДИСПЕРСИЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ По аналогии с дискретной случайной величиной, можно ввести понятие дисперсии для непрерывной
- 16. ДИСПЕРСИЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Дисперсией непрерывной случайной величины называют математическое ожидание квадрата разности между этой случайной
- 18. Скачать презентацию















 Повторение Обыкновенные дроби. Основное свойство дроби. Из частного (деления) Дробной чертой Числитель Знаменатель Сравни
Повторение Обыкновенные дроби. Основное свойство дроби. Из частного (деления) Дробной чертой Числитель Знаменатель Сравни Предметы геометрической формы. Логические задания
Предметы геометрической формы. Логические задания Системы уравнений и методы их решения
Системы уравнений и методы их решения Презентация на тему ГРАФИК ДВИЖЕНИЯ
Презентация на тему ГРАФИК ДВИЖЕНИЯ  Анализ уравнения на соответствие графику
Анализ уравнения на соответствие графику Числовые головоломки
Числовые головоломки Ряды Фурье
Ряды Фурье Сложение и вычитание дробей
Сложение и вычитание дробей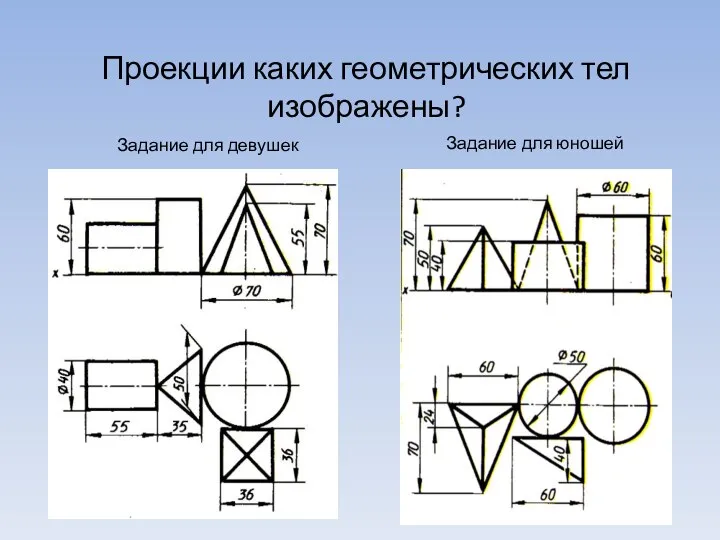 Проекции каких геометрических тел изображены?
Проекции каких геометрических тел изображены? День 3. Продающие тексты. Практика. Что продаем?
День 3. Продающие тексты. Практика. Что продаем? 8 класс
8 класс Площадь полной поверхности призмы
Площадь полной поверхности призмы Окружность и круг. Задачи
Окружность и круг. Задачи Презентация на тему Переменная
Презентация на тему Переменная  Прямые на плоскости
Прямые на плоскости Число π
Число π Квадратные неравенства
Квадратные неравенства Презентация на тему Теория вероятностей и комбинаторные правила
Презентация на тему Теория вероятностей и комбинаторные правила  Задачи ФИПИ
Задачи ФИПИ Презентация на тему Таблицы умножения и деления с числом 6
Презентация на тему Таблицы умножения и деления с числом 6  Математическая статистика
Математическая статистика Законы сложения и умножения
Законы сложения и умножения Элементы теории вероятности в практических задачах
Элементы теории вероятности в практических задачах Решение задач с параметрами
Решение задач с параметрами Презентация на тему Решение задач с помощью квадратных уравнений
Презентация на тему Решение задач с помощью квадратных уравнений  Преобразование графиков функции
Преобразование графиков функции Измерение объема жидких и сыпучих веществ с помощью условной меры масс
Измерение объема жидких и сыпучих веществ с помощью условной меры масс Теорема Виета. Урок систематизации, обобщения и контроля знаний
Теорема Виета. Урок систематизации, обобщения и контроля знаний