Содержание
- 2. . . . . Презентация На тему: «Дифференциальные уравнения первого порядка» Подготовил студент группы К-11 Свиноренко
- 3. План: Простейшие дифференциальные уравнения первого порядка. Понятие дифференциального уравнения. ТЕОРЕМА КОШИ. Самый простой пример… Небольшой вопросик.
- 4. Простейшие дифференциальные уравнения первого порядка. К ним относят: 1. Простейшие дифференциальные уравнения первого порядка: y’ =f(x)
- 5. Уравнение вида: называется ДУ первого порядка. Где х – независимая переменная; у– неизвестная функция; у‘ –
- 6. Если из уравнения можно выразить производную неизвестной функции, то оно примет вид: Это уравнение называется ДУ
- 7. Решением ДУ первого порядка называется функция у=φ(х), определенная на некотором интервале (a,b), которая при подстановке ее
- 8. ТЕОРЕМА КОШИ (о существовании и единственности решения ДУ) Пусть дано ДУ Если функция f(x,y) и ее
- 9. Условия, задающие значения функции в фиксированной точке называются начальными условиями (условиями Коши):
- 10. Задача решения уравнения называется задачей Коши. удовлетворяющего условию В некоторых случаях, если условия теоремы Коши не
- 11. Рассмотрим уравнение Правая часть этого уравнения удовлетворяет всем условиям теоремы Коши во всех точках плоскости x,0,y:
- 12. Что значит решить дифференциальное уравнение ? Решить дифференциальное уравнение – это значит, найти множество всех функций,
- 13. Даа…. Это несомненно правильный ответ!!! Давай дальше!))) Нажми сюда
- 14. Ты серьезно ??? Давай назад.
- 15. К сожалению это конец (((
- 17. Скачать презентацию














 Функция y=k/x, её график и свойства. 8 класс. Урок 2
Функция y=k/x, её график и свойства. 8 класс. Урок 2 Квадратный трехчлен. Самостоятельная работа
Квадратный трехчлен. Самостоятельная работа Решение задач разными арифметическими способами
Решение задач разными арифметическими способами Проценты
Проценты HMM выравнивание
HMM выравнивание Повторюємо арифметичні дії множення і ділення
Повторюємо арифметичні дії множення і ділення Презентация на тему Теорема о трех перпендикулярах
Презентация на тему Теорема о трех перпендикулярах  Решение задач. Геометрия, 8 класс
Решение задач. Геометрия, 8 класс Математика 1 класс
Математика 1 класс Решение прикладных задач с помощью свойств квадратичной функции
Решение прикладных задач с помощью свойств квадратичной функции Решение задач по теме Многогранники
Решение задач по теме Многогранники Критическое мышление
Критическое мышление Интерактивные Крестики-нолики. Задачи на готовых чертежах. Сумма углов треугольника
Интерактивные Крестики-нолики. Задачи на готовых чертежах. Сумма углов треугольника Понятие дифференциала. Приложение дифференциала
Понятие дифференциала. Приложение дифференциала Задача о баскетболисте. Расчетная работа №1
Задача о баскетболисте. Расчетная работа №1 Прибавление и вычитание числа 3. Помоги белочке
Прибавление и вычитание числа 3. Помоги белочке Квадратные уравнения
Квадратные уравнения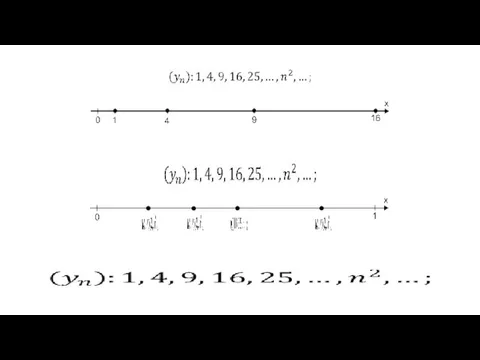 Пояснения к определению предела последовательности
Пояснения к определению предела последовательности Признаки равенства треугольников
Признаки равенства треугольников Фрактальное изображение
Фрактальное изображение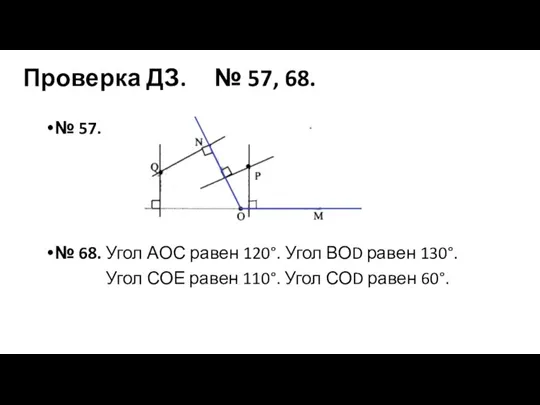 Подготовка к контрольной работе
Подготовка к контрольной работе История возникновения геометрии как науки
История возникновения геометрии как науки Геометрические преобразования в пространстве
Геометрические преобразования в пространстве Презентация на тему Длина окружности и площадь круга (9 класс)
Презентация на тему Длина окружности и площадь круга (9 класс)  СМО
СМО Collatz Conjecture
Collatz Conjecture Найти корень уравнения. Тест. Задания В5, ЕГЭ по математике
Найти корень уравнения. Тест. Задания В5, ЕГЭ по математике Упражнения по планиметрии на готовых чертежах. VII класс
Упражнения по планиметрии на готовых чертежах. VII класс