Слайд 2…Геометрия – это просто алгебра,
воплощенная в фигурах.
Софи Жермен (1776-1831)
Алгоритм применения

метода координат к решению геометрических задач
Выбираем в пространстве систему координат из соображений удобства выражения координат и наглядности изображения.
Находим координаты необходимых для нас точек.
Решаем задачу, используя основные задачи метода координат.
Переходим от аналитических соотношений к геометрическим.
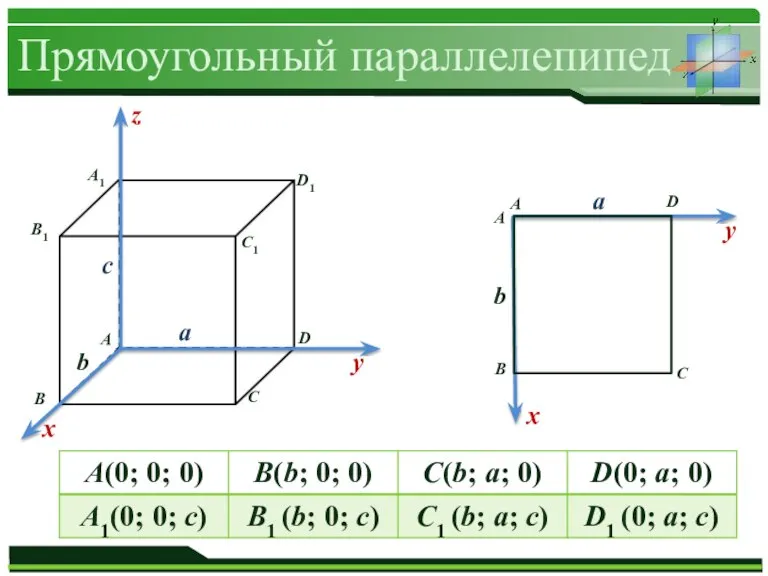
Слайд 3Прямоугольный параллелепипед
а
а
b
с
b
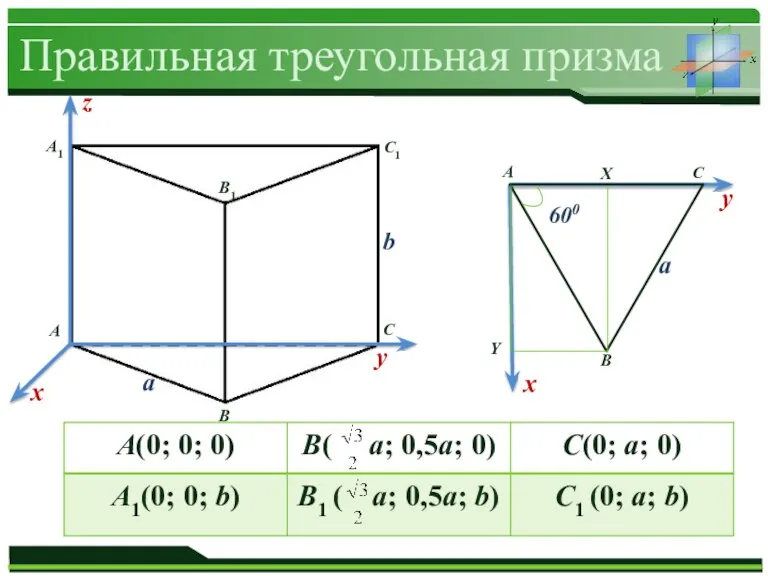
Слайд 4Правильная треугольная призма
а
а
b
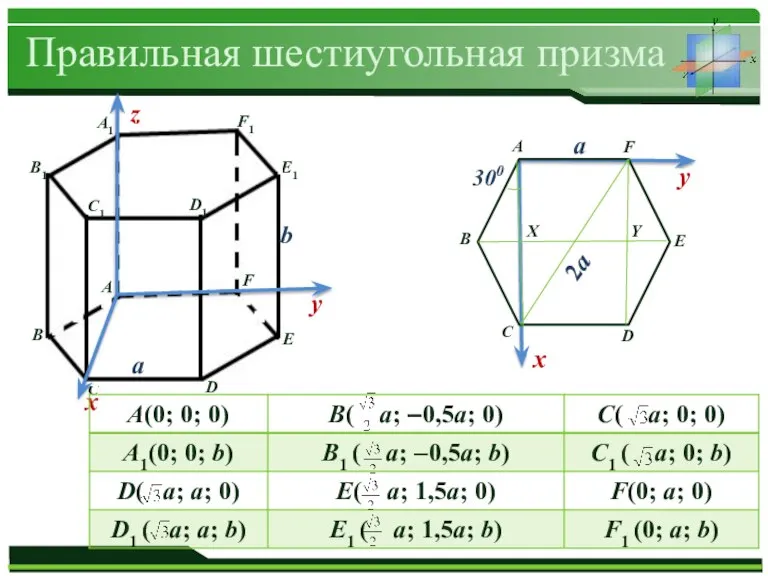
Слайд 5Правильная шестиугольная призма
а
а
b
Слайд 6O
O
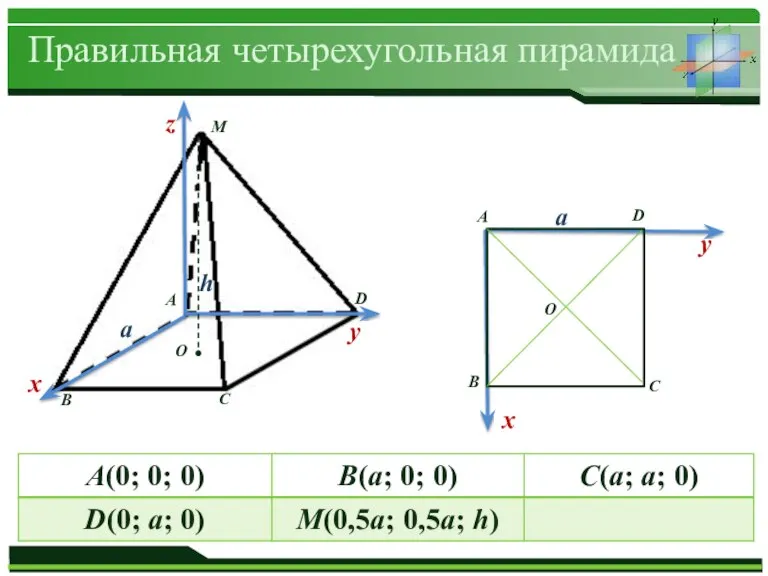
Правильная четырехугольная пирамида
а
а
h
Слайд 7O
O
а
h
а
Правильная треугольная пирамида
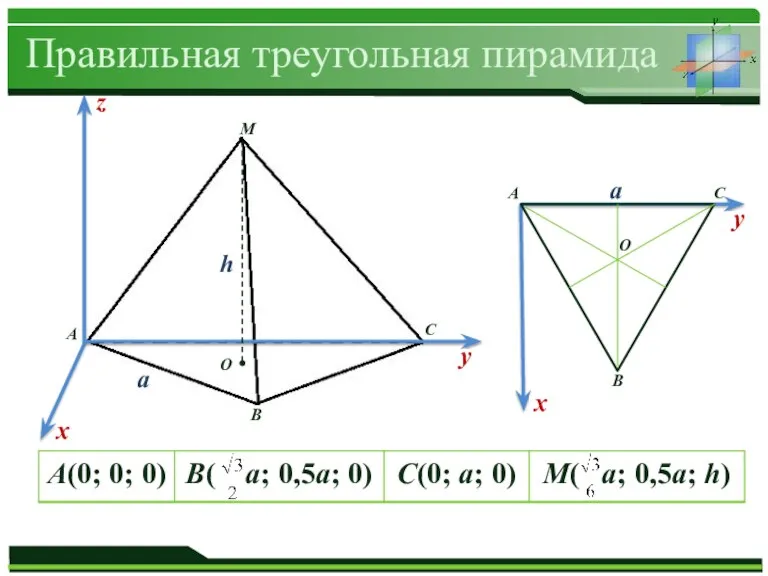
Слайд 8O
O
а
а
h
Правильная шестиугольная пирамида
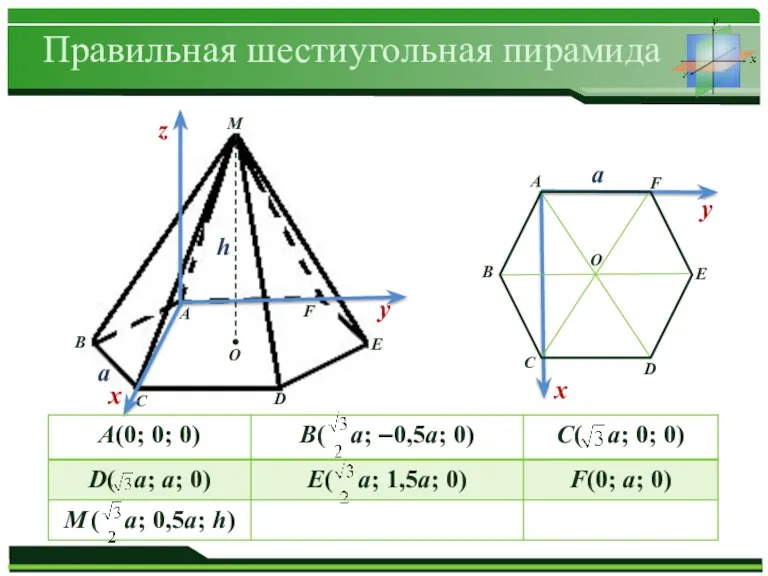
Слайд 9n
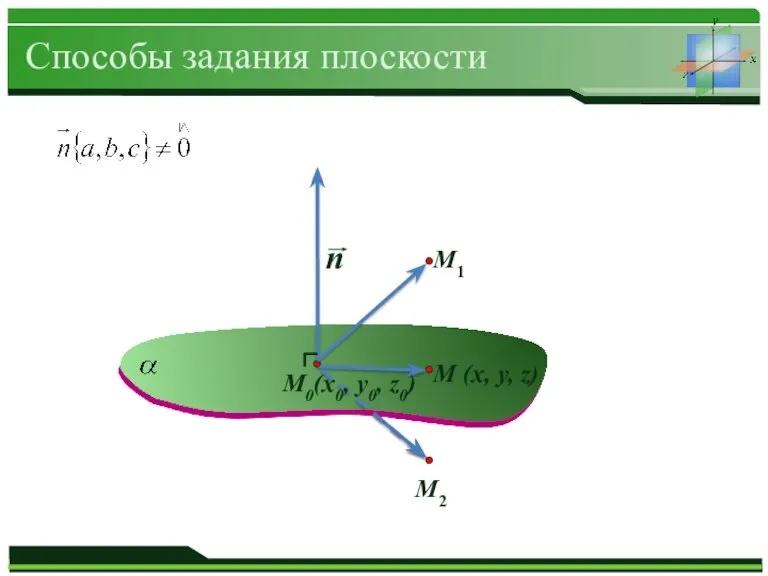
Способы задания плоскости
М1
М2
М (x, y, z)
М0(x0, y0, z0)
Слайд 10М(x0, y0, z0)
n
Уравнение плоскости α, проходящей через точку М0(x0, y0, z0) и

перпендикулярной вектору :
Общее уравнение плоскости:
где – нормальный вектор
плоскости.
Слайд 11М0(x0, y0, z0)
а
Способы задания прямой
Каноническое уравнение прямой l, заданной точкой М0(x0, y0,

z0) и направляющим вектором
:
Слайд 12М1(x1, y1, z1)
а
Способы задания прямой
Уравнение прямой, заданной двумя своими точками М1(x1, y1,

z1) и М2(x2, y2, z2):
М2(x2, y2, z2)











 Путешествие в город Дробей на проспект Умножения. 6 класс
Путешествие в город Дробей на проспект Умножения. 6 класс Действительный анализ. Теорема Лебега (примеры). Измеримые множества
Действительный анализ. Теорема Лебега (примеры). Измеримые множества Как умножали египтяне
Как умножали египтяне Площадь многоугольника
Площадь многоугольника Решение систем неравенств с одной переменной
Решение систем неравенств с одной переменной Оценка математического ожидания и дисперсии отклика в отдельных точках факторного пространства
Оценка математического ожидания и дисперсии отклика в отдельных точках факторного пространства Полигон частот в математической статистике
Полигон частот в математической статистике Лінейныя ўраўненні з адной зменнай
Лінейныя ўраўненні з адной зменнай Расчёт скорости официанта от кассы до столика
Расчёт скорости официанта от кассы до столика Объём тела
Объём тела Теорема о плоскости, касательной к шару
Теорема о плоскости, касательной к шару Площадь круга и секторов
Площадь круга и секторов Куб
Куб Корень степени n
Корень степени n Построение биссектрисы угла. Билеты
Построение биссектрисы угла. Билеты Урок математики 20.09
Урок математики 20.09 Презентация на тему РЕШЕНИЕ ДРОБНЫХ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ
Презентация на тему РЕШЕНИЕ ДРОБНЫХ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ  Занимательные математические задания
Занимательные математические задания Сравнение групп предметов. Свойства предметов (1 класс)
Сравнение групп предметов. Свойства предметов (1 класс) Математическая модель колонны многокомпонентной ректификации. Лекция 9
Математическая модель колонны многокомпонентной ректификации. Лекция 9 Производная в заданиях уровня В. ЕГЭ
Производная в заданиях уровня В. ЕГЭ Неопределенный интеграл
Неопределенный интеграл Презентация на тему Простые числа
Презентация на тему Простые числа  История г. Колпашева в примерах и задачах
История г. Колпашева в примерах и задачах Сочетания. Свойства сочетаний. Бином Ньютона
Сочетания. Свойства сочетаний. Бином Ньютона Основные понятия теории вероятностей
Основные понятия теории вероятностей Возрастание и убывание функций. Экстремумы
Возрастание и убывание функций. Экстремумы Памятка по оформлению краткой записи к задачам (1 класс)
Памятка по оформлению краткой записи к задачам (1 класс)