Пирамида. Её элементы. Правильная пирамида. Усечённая пирамида

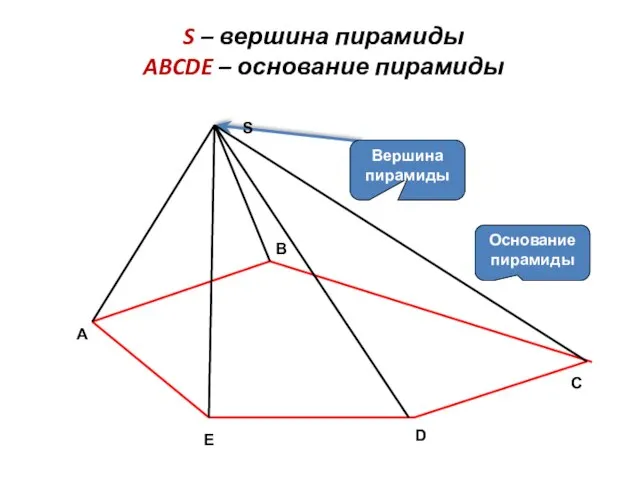
S – вершина пирамиды
ABCDE – основание пирамиды
C
Основание пирамиды
Вершина пирамиды

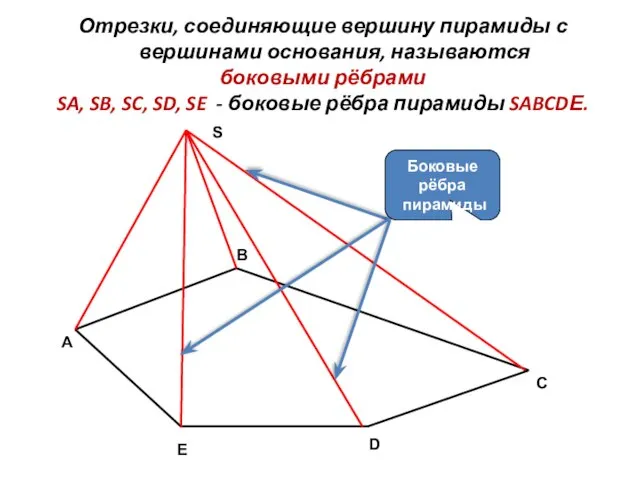
C
Отрезки, соединяющие вершину пирамиды с вершинами основания, называются
боковыми рёбрами
SA, SB, SC, SD, SE - боковые рёбра пирамиды SABCDЕ.
Боковые рёбра
пирамиды

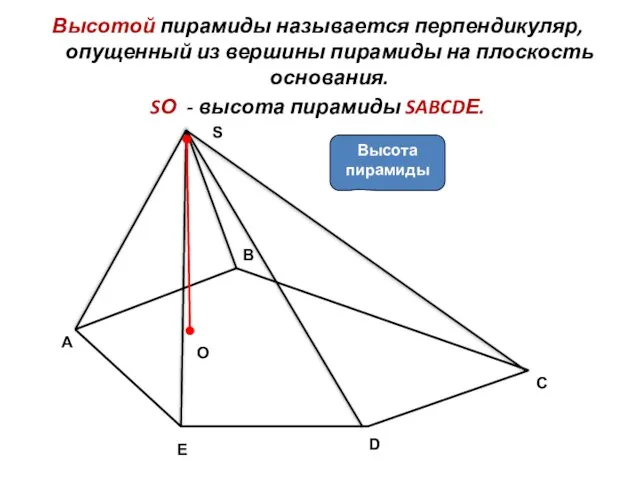
C
Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
SО - высота пирамиды SABCDЕ.
О
Высота пирамиды

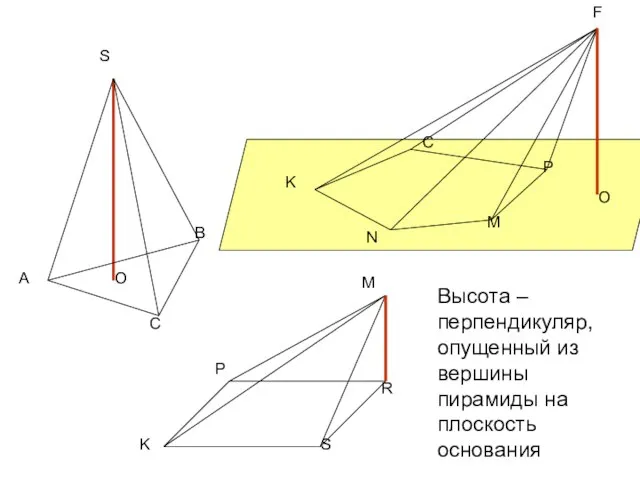
O
O
Высота – перпендикуляр, опущенный из вершины пирамиды на плоскость основания

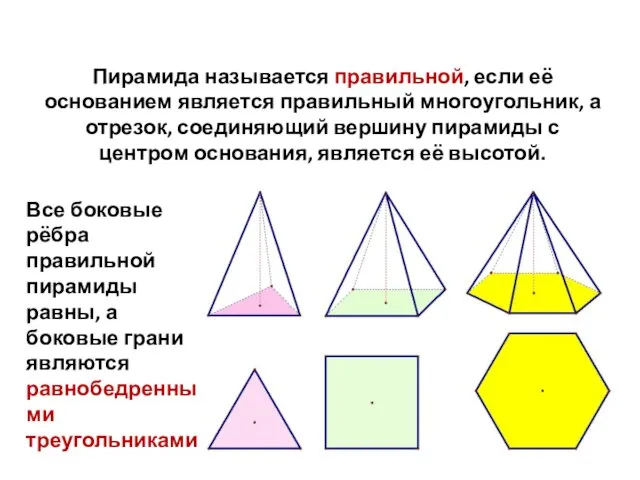
Пирамида называется правильной, если её основанием является правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является её высотой.
Все боковые рёбра правильной пирамиды равны, а боковые грани являются равнобедренными треугольниками

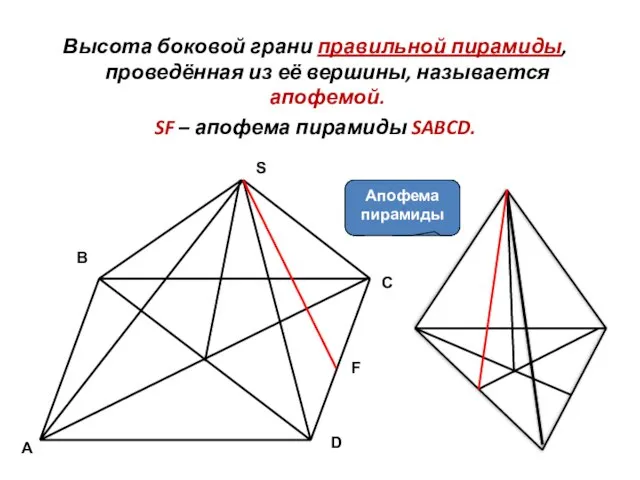
Высота боковой грани правильной пирамиды, проведённая из её вершины, называется апофемой.
SF – апофема пирамиды SABCD.
Апофема пирамиды
Апофема пирамиды

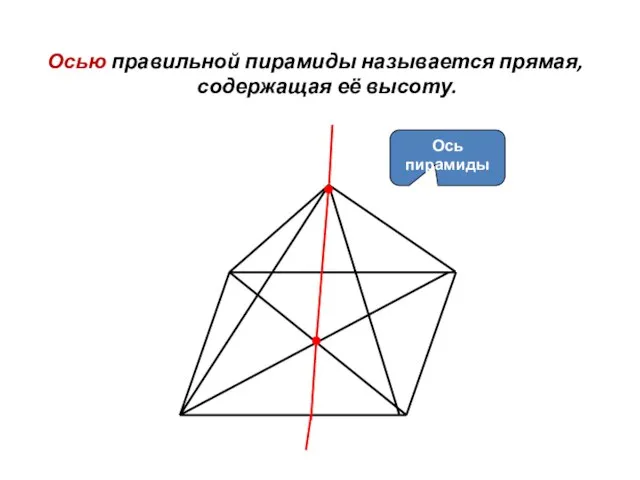
Осью правильной пирамиды называется прямая, содержащая её высоту.
Ось пирамиды

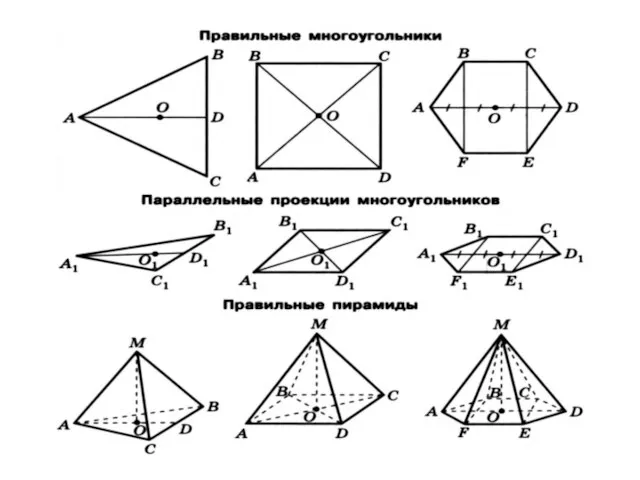
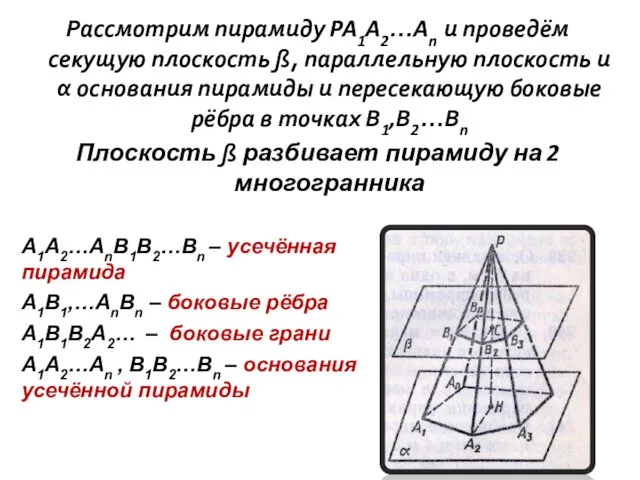
Рассмотрим пирамиду PA1A2…An и проведём секущую плоскость ß, параллельную плоскость и α основания пирамиды и пересекающую боковые рёбра в точках В1,В2…Вn
Плоскость ß разбивает пирамиду на 2 многогранника
A1A2…AnВ1В2…Вn – усечённая пирамида
A1В1,…AnВn – боковые рёбра
A1В1В2A2… – боковые грани
A1A2…An , В1В2…Вn – основания усечённой пирамиды

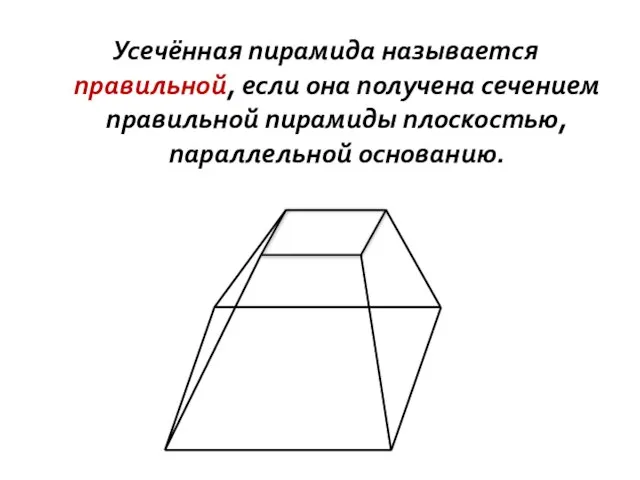
Усечённая пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию.

Площадь полной поверхности пирамиды равна сумме площади боковой поверхности и площади основания:
Боковой поверхностью пирамиды называется сумма площадей её боковых граней.

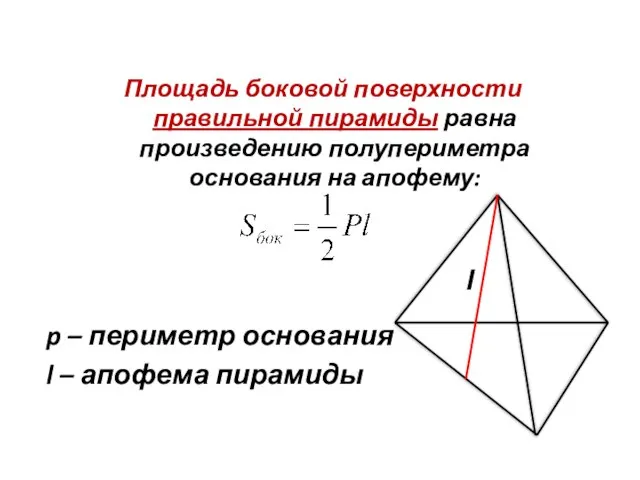
Площадь боковой поверхности правильной пирамиды равна произведению полупериметра основания на апофему:
p – периметр основания
l – апофема пирамиды

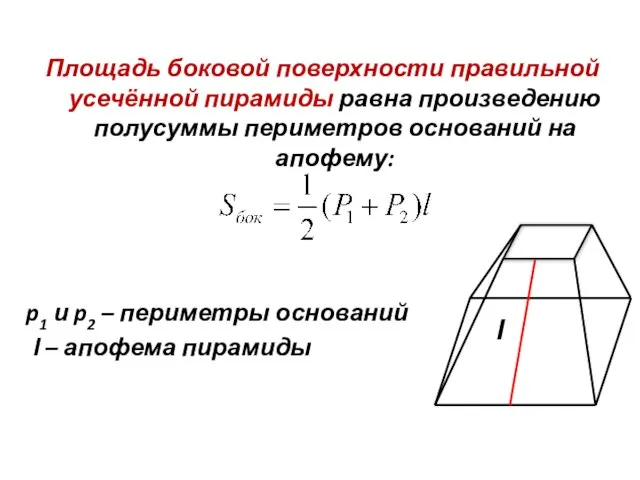
Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему:
p1 и p2 – периметры оснований
l – апофема пирамиды
l

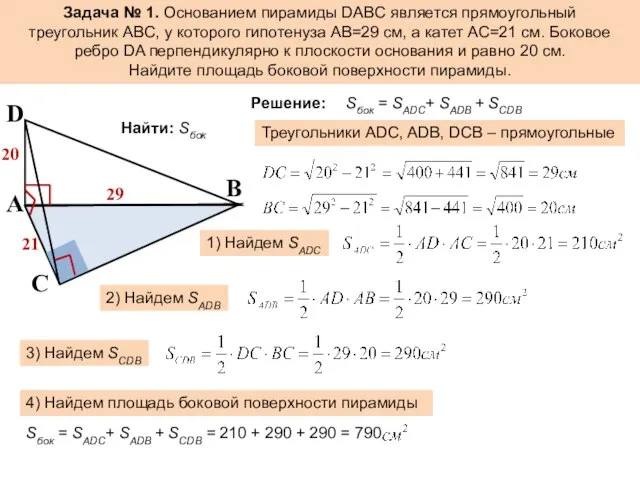
B
Задача № 1. Основанием пирамиды DABC является прямоугольный
треугольник ABC, у которого гипотенуза AB=29 см, а катет АС=21 см. Боковое ребро DA перпендикулярно к плоскости основания и равно 20 см.
Найдите площадь боковой поверхности пирамиды.
Найти: Sбок
Решение:
Треугольники ADC, ADB, DCB – прямоугольные
1) Найдем SADC
4) Найдем площадь боковой поверхности пирамиды
C
A
D
29
21
20
Sбок = SADC+ SADB + SCDB
Sбок = SADC+ SADB + SCDB = 210 + 290 + 290 = 790
2) Найдем SADB
3) Найдем SCDB