Вспомним планиметрию

ВСПОМНИМ ПЛАНИМЕТРИЮ
Каково может быть взаимное расположение двух прямых на плоскости?
а
b
а
b
Какие прямые в планиметрии называются перпендикулярными?
а
b

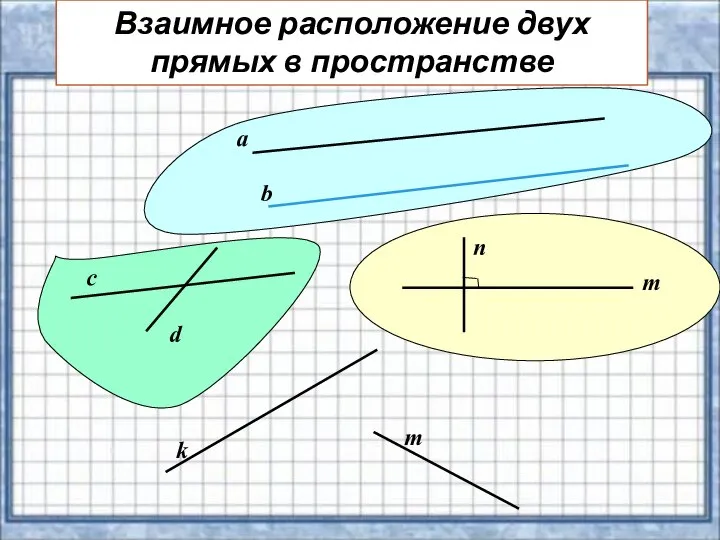
Взаимное расположение двух прямых в пространстве
а
b
с
d
m
n
k
m

Тема урока: «Перпендикулярность прямых в пространстве»

Две прямые называются перпендикулярными, если они пересекаются под прямым углом
m
n
n m
∠ (nm) = 900

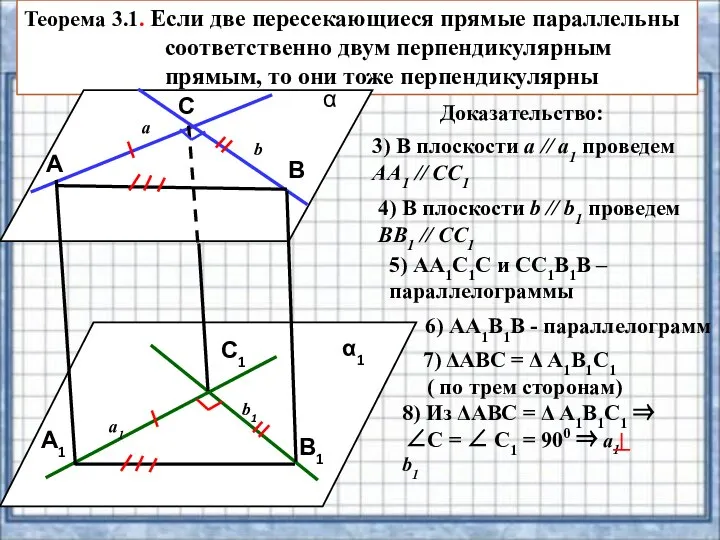
Теорема 3.1. Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они тоже перпендикулярны
Дано: a b, a1 ∩ b1 в точке С1 , a // a1 , b // b1
Доказать: a1 b1
Доказательство:
а1
b1
С
α
α1
С1
а
b
1)Допустим a, b∈α , a1, b1 ∈α1
2) α // α1 (по признаку параллельности плоскостей)

Теорема 3.1. Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они тоже перпендикулярны
Доказательство:
а1
b1
А
В
С
А1
В1
α
α1
С1
а
b
3) В плоскости a // a1 проведем АА1 // СС1
4) В плоскости b // b1 проведем ВВ1 // СС1
5) АА1С1С и СС1В1В –
параллелограммы
6) АА1В1В - параллелограмм
7) ΔАВС = Δ А1В1С1
( по трем сторонам)
8) Из ΔАВС = Δ А1В1С1 ⇒
∠С = ∠ С1 = 900 ⇒ a1 b1