Слайд 2Метод моментов решения операторных уравнений
Приближенное решение ищем в виде
Неизвестные коэффициенты находим из

условия
(1)
(2)
(3)
(4)
Получаем СЛАУ
Слайд 3Метод моментов решения интегрального уравнения Фредгольма II рода
(5)
Приближенное решение ищем в виде
(6)
Получаем

Слайд 4(8)
Для погрешности приближенных решений справедливы оценки

Слайд 5Интегральное уравнение I-го рода с логарифмической особенностью в ядре
(9)
Приближенное решение ищем в

виде
(10)
Получаем СЛАУ
(11)
Слайд 7Метод моментов решения сингулярного интегродифференциального уравнения
(12)
(13)
.
Приближенное решение ищем в виде
(14)

Слайд 8(15)
Получаем СЛАУ
(16)
Справедливы оценки








 Основные формулы для Огэ по математике
Основные формулы для Огэ по математике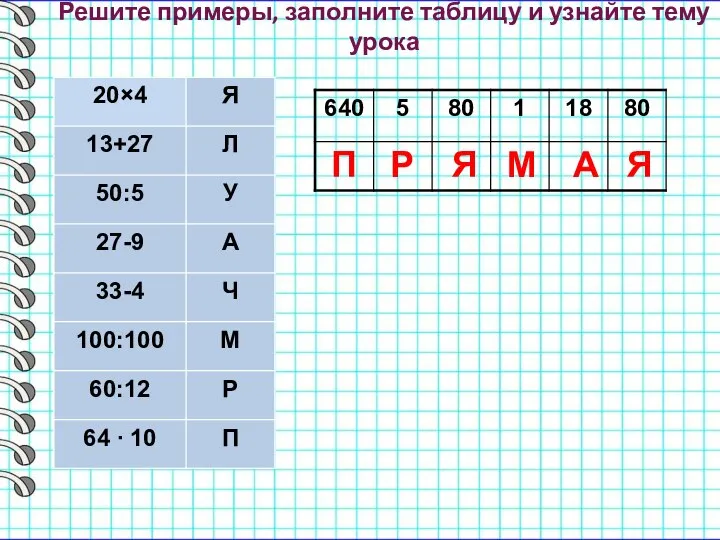 Прямая. Плоскость
Прямая. Плоскость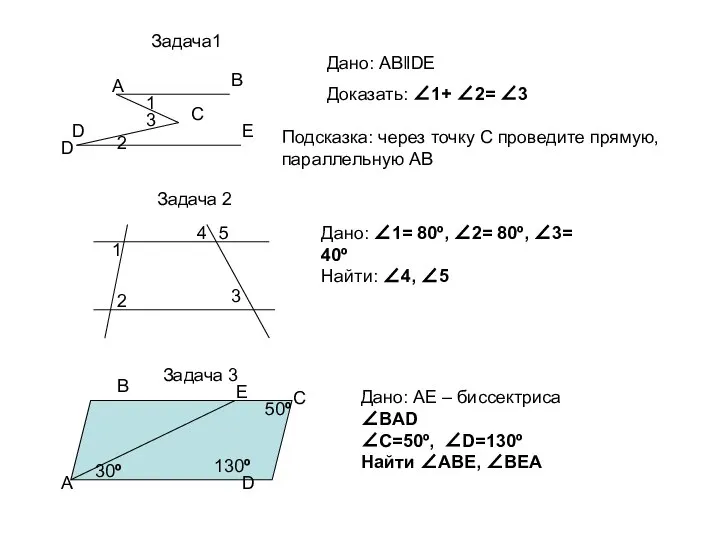 Параллельные прямые (тест)
Параллельные прямые (тест) Знакомство с линейкой
Знакомство с линейкой Параллельность_прямых_в_пространстве_2019
Параллельность_прямых_в_пространстве_2019 Презентация на тему Приёмы устного решения квадратного уравнения
Презентация на тему Приёмы устного решения квадратного уравнения  Презентация на тему Свойства функций и их графики
Презентация на тему Свойства функций и их графики  Многоугольники
Многоугольники Графики функций
Графики функций Построение графиков функций
Построение графиков функций Повторение. Математика, 1 класс
Повторение. Математика, 1 класс Презентация на тему Решение иррациональных уравнений
Презентация на тему Решение иррациональных уравнений  Проценты. Задачи
Проценты. Задачи 2._3
2._3 Математика в ребусах, загадках и кроссвордах
Математика в ребусах, загадках и кроссвордах Сравнение натуральных чисел
Сравнение натуральных чисел Логарифмы. Определение
Логарифмы. Определение Математическая игра
Математическая игра Презентация на тему Нумерация многозначных чисел (4 класс)
Презентация на тему Нумерация многозначных чисел (4 класс)  Параллельности прямой и плоскости. Параллельности плоскостей
Параллельности прямой и плоскости. Параллельности плоскостей Логарифмическая функция. Свойства, график. Решение примеров
Логарифмическая функция. Свойства, график. Решение примеров Формулы Крамера. Системы линейных алгебраических уравнений
Формулы Крамера. Системы линейных алгебраических уравнений Площадь прямоугольника
Площадь прямоугольника Прямоугольный треугольник. Теорема Пифагора
Прямоугольный треугольник. Теорема Пифагора Презентация на тему История возникновения счета
Презентация на тему История возникновения счета  1_urok_ponyatie_vektora
1_urok_ponyatie_vektora Комплексные числа. Задачи
Комплексные числа. Задачи Задачи на проценты в заданиях ГИА
Задачи на проценты в заданиях ГИА