вершина. Известно, что AB = 1, а SR = 2. Найдите площадь боковой поверхности.
Решение
Отмечаем упомянутые в условии точки и отрезки на чертеже пирамиды. Отрезок SR принадлежит боковой грани, поэтому наряду с пирамидой и основанием, начертим и её - треугольник BSC.
По формуле площади боковой поверхности правильной пирамиды Sб = Pосн· l/2.
Так как пирамида правильная, то ΔBSC - равнобедренный, и линия, соединяющая середину его основания с вершиной, является не только медианой, но и высотой этого треугольника, а значит апофемой пирамиды (l = 2).
Периметр основания - сумма всех сторон треугольника ABC. Треугольник равносторонний, следовательно
Pосн = AB + BC + AC = 3·AB = 3·1 = 3.
Таким образом Sб = Pосн· l/2 = 3·2/2 = 3. Ответ: 3

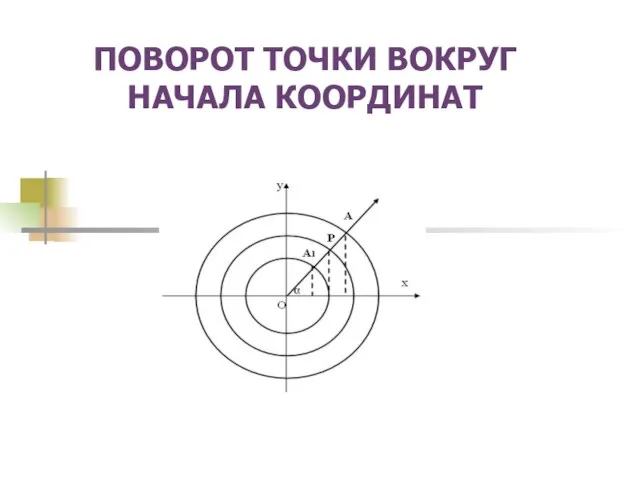 ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ
ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ Многогранники в профессиях
Многогранники в профессиях Решение задач на проценты
Решение задач на проценты Определение производной. Правила вычисления производных. Таблица производных
Определение производной. Правила вычисления производных. Таблица производных Решение задач на t°С воздуха и АД
Решение задач на t°С воздуха и АД Построение сечений тетраэдра и параллелепипеда
Построение сечений тетраэдра и параллелепипеда Упрощение и нахождение значения выражений содержащих степени
Упрощение и нахождение значения выражений содержащих степени Натуральный логарифм. Функция y=ln x, её свойства, график, дифференцирование
Натуральный логарифм. Функция y=ln x, её свойства, график, дифференцирование Первый признак равенства треугольников
Первый признак равенства треугольников 3.7. Непрерывность функции
3.7. Непрерывность функции Практикум по решению задач
Практикум по решению задач Признак перпендикулярности плоскостей
Признак перпендикулярности плоскостей Рациональные уравнения
Рациональные уравнения Буквенная запись свойств действий над числами
Буквенная запись свойств действий над числами Среднее арифметическое
Среднее арифметическое Состав чисел в пределах 10. Урок №80
Состав чисел в пределах 10. Урок №80 Функция y = x2 и её график
Функция y = x2 и её график Предел_посл_1
Предел_посл_1 Радианная мера угла. Синус, косинус, тангенс числа
Радианная мера угла. Синус, косинус, тангенс числа Презентация на тему Сложение целых чисел
Презентация на тему Сложение целых чисел  Деление на 3
Деление на 3 Числовые равенства и их свойства
Числовые равенства и их свойства Взаимно обратные функции
Взаимно обратные функции Окружность. Задачи на построение
Окружность. Задачи на построение Понятие десятичной дроби
Понятие десятичной дроби Численное решение обыкновенных дифференциальных уравнений. Краевая задача
Численное решение обыкновенных дифференциальных уравнений. Краевая задача Логарифмы вокруг нас
Логарифмы вокруг нас Графики тригонометрических функций
Графики тригонометрических функций