Численное решение дифференциальных уравнений

Линейные дифференциальные уравнения в частных производных
Пусть искомая функция зависит от нескольких независимых переменных
,
Уравнение, связывающее искомую функцию, независимые переменные и частные производные от искомой функции, называется дифференциальным уравнением с частными производными.
Здесь F -- данная функция своих аргументов.
Порядок старшей частной производной, входящей в уравнение, называется порядком уравнения с частными производными.

Дифференциальное уравнение с частными производными первого порядка с независимыми переменными может быть записано в форме:
Общее решение дифференциального уравнения с частными производными, вообще говоря, может зависеть от некоторых произвольных (гладких) функций.

Классификация дифференциальных уравнений в зависимости от физического смысла решаемых задач:
Уравнение диффузии
Уравнение теплопроводности
Волновое уравнение

ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА
Существование и единственность решения
Обыкновенное дифференциальное уравнение первого порядка, разрешённое относительно производной, имеет вид
Решением данного обыкновенного дифференциального уравнения называется функция ϕ(x) , подстановка которой в уравнение обращает его в тождество:
График решения y= ϕ(x) называется интегральной кривой.
Задача Коши для дифференциального уравнения
состоит в том, чтобы найти решение уравнения, удовлетворяющее начальному условию

Частному решению соответствует одна из интегральных кривых, проходящая через точку
Теорема.
Пусть функция f(x, y) – правая часть уравнения y’=f(x, y) – непрерывна вместе со своей частной производной
в некоторой области D на плоскости.
Тогда при любых начальных данных задача Коши имеет единственное решение y= ϕ(x) .
Численное решение задачи Коши состоит в том, чтобы получить искомое решение ϕ(x) в виде таблицы его приближённых значений для заданных значений аргумента x на некотором отрезке [a, b] :

Точки называют узловыми точками, а множество этих точек называют сеткой на отрезке [a, b].
Будем использовать равномерную сетку с шагом h:
Приближённые значения численного решения задачи Коши в узловых точках xi обозначим через yi.
Таким образом,
Для любого численного метода решения задачи Коши начальное условие выполняется точно:
Величина погрешности численного метода решения задачи Коши на сетке отрезка [a, b] оценивается величиной

Говорят, что численный метод имеет p-й порядок точности по шагу h на сетке, если расстояние d можно представить в виде степенной функции от h :
где C – некоторая положительная постоянная, зависящая от f(x, y) и от рассматриваемого метода.

Метод Эйлера

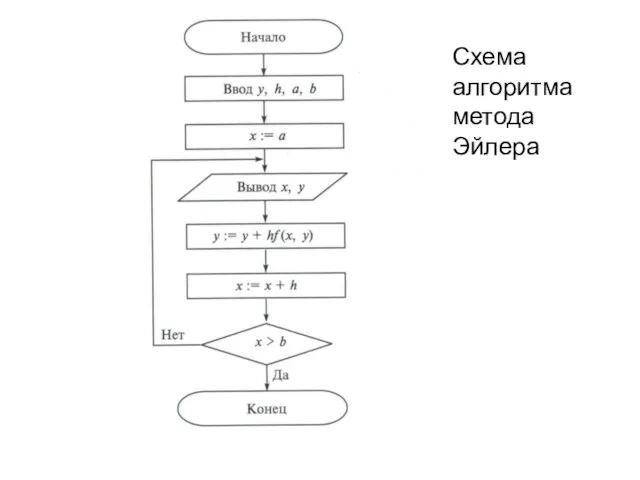
Графической иллюстрацией приближённого решения является ломаная, соединяющая последовательно точки
, которую называют ломаной Эйлера

Погрешность метода Эйлера

Схема алгоритма метода Эйлера

Пример 1

Решение

Модификации метода Эйлера

Второй модифицированный метод Эйлера

Пример 2

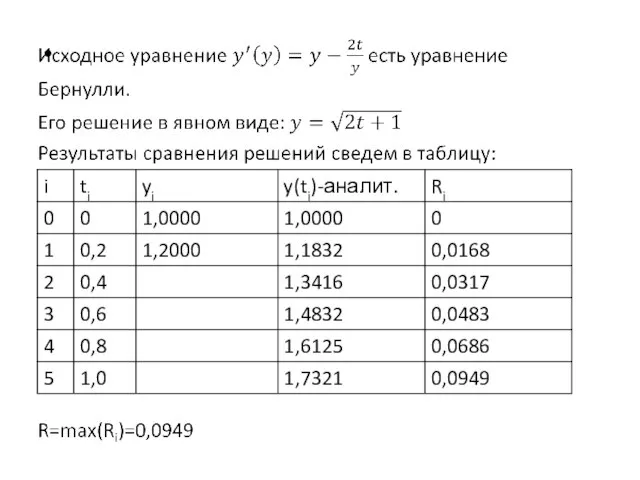
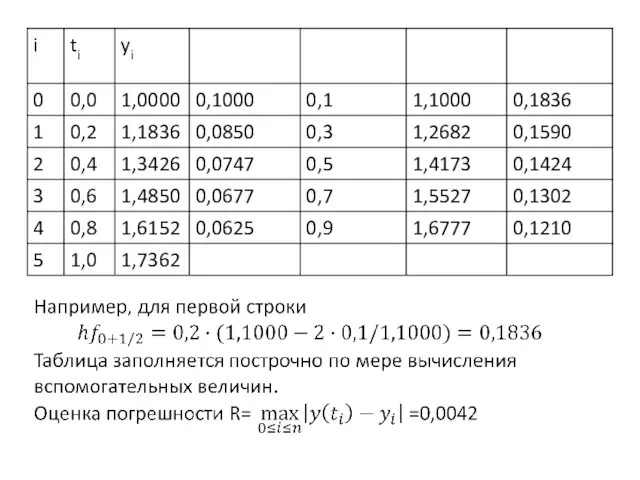
Решение 1-ым модифицированным методом Эйлера

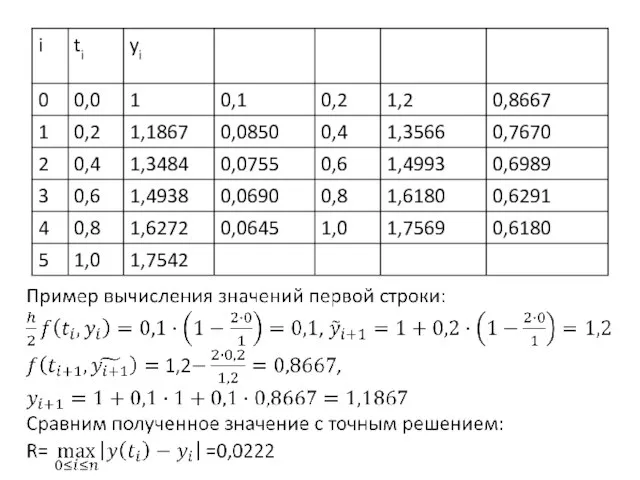
Решение 2-ым модифицированным методом Эйлера

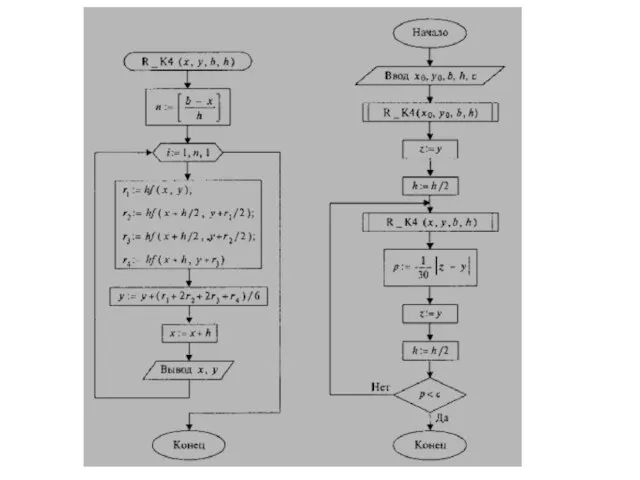
Метод Рунге-Кутта
Основная идея метода – вместо использования в расчётных формулах частных производных функции f(x, y) использовать саму функцию, но на каждом шаге вычислять её значения в нескольких точках.
Возможно применение формул Рунге-Кутта разных порядков. Наиболее часто применяются на практике формулы Рунге Кутта 4-го порядка точности.

Расчетные формулы метода Рунге – Кутта четвертого порядка точности:
Оценка погрешности:
.

Пример 3

Решение

Дифференциальные уравнения второго порядка. Краевые задачи.
На практике часто приходится решать задачи, когда требуется, чтобы искомая функция имела бы заданные значения на границах отрезка, на котором рассматривается решение.
Такие задачи, называемые краевыми, получаются при решении уравнений высших порядков или систем уравнений.
Рассмотрим линейное дифференциальное уравнение второго порядка
Краевая задача состоит в отыскании решения
уравнения на отрезке [a, b] , удовлетворяющего на концах отрезка условиям

Методы решения краевых задач
Аналитические методы имеются лишь для решения узкого класса уравнений, в частности для решения линейных дифференциальных уравнений с постоянными коэффициентами, которые широко используются при исследовании различных физических процессов
Приближенные методы разрабатывались еще задолго до появления компьютеров. Однако многие из них до сих пор не утратили своего значения. Это методы коллокаций, наименьших квадратов, метод Галеркина и др.
Численные методы решения краевой задачи можно разделить на две группы: сведение (редукция) решения краевой задачи к последовательности решений задач Коши и непосредственное применение конечно-разностных методов.