Содержание
- 2. 2, 4, 6, 8, 10, . . . 5,10,15,20,25, … 3, -1, -5, -9, -13,… Последовательностью
- 3. Обозначение членов последовательности 1, 2, 3, 4, 5, …, n-1, n, n+1,… a1, a2, a3, a4,
- 4. Рекуррентный способ задания последовательности Название способа произошло от слова «recurro» - возвращаться. Рекуррентной называется формула, выражающая
- 5. Таким образом, числовая последовательность, заданная рекуррентной формулой является арифметической прогрессией Определение. Числовая последовательность, каждый член которой,
- 6. №174(2), №235 Формула n- члена №176(2,4), №177(3) Арифметическая прогрессия
- 7. Геометрическая прогрессия Определение. Числовая последовательность, каждый член которой, начиная со второго, равен произведению предыдущего члена и
- 8. Геометрическая прогрессия – это числовая последовательность, заданная рекуррентной формулой Формула n- члена №244(1,3), №243(1)
- 9. Подведём итог Арифметическая прогрессия Геометрическая прогрессия Последовательность, в которой каждый член, начиная со второго, равен предыдущему
- 10. Формула n-го члена прогрессии an=a1+d(n-1) Дано: a1 = 7, d = 5 Найти: a4 a4 =
- 12. Скачать презентацию

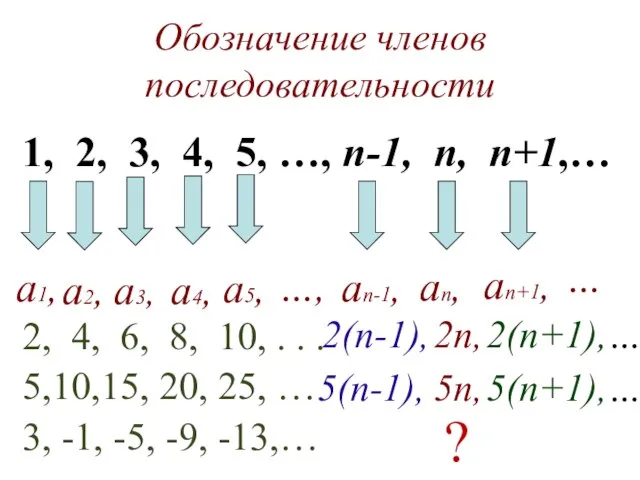







 Таблица умножения числа 2 и на 2
Таблица умножения числа 2 и на 2 Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1
Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1 Статистический анализ результатов мониторинга
Статистический анализ результатов мониторинга Вынесение общего множителя за скобки. 6 класс
Вынесение общего множителя за скобки. 6 класс Степень с натуральным показателем. Задания
Степень с натуральным показателем. Задания Решение уравнений. Элективный курс. Алгебра 11 класс. Урок 2
Решение уравнений. Элективный курс. Алгебра 11 класс. Урок 2 Принадлежность точки выделенной области. 10 класс
Принадлежность точки выделенной области. 10 класс Уравнения, системы уравнений. Задание №9
Уравнения, системы уравнений. Задание №9 Теория расписаний. Минимизация приоритето-порождающих функций
Теория расписаний. Минимизация приоритето-порождающих функций Математическое описание случайных явлений
Математическое описание случайных явлений Операции над множествами
Операции над множествами Презентация на тему Занимательная математика (5 класс)
Презентация на тему Занимательная математика (5 класс)  Учимся считать. Интерактивный тренажёр
Учимся считать. Интерактивный тренажёр Упрощение выражений
Упрощение выражений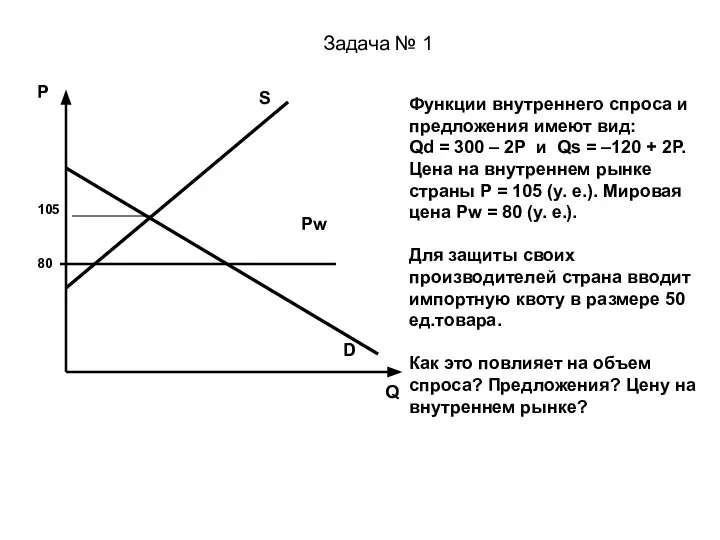 Функции внутреннего спроса и предложения. Разбор задач
Функции внутреннего спроса и предложения. Разбор задач Презентация на тему Свойства логарифмов (10 класс)
Презентация на тему Свойства логарифмов (10 класс)  Математика в профессии сварщика
Математика в профессии сварщика Задачи на перебор вариантов
Задачи на перебор вариантов Прикладной количественный анализ заголовков
Прикладной количественный анализ заголовков Путешествие в историю математики. Решение старинных задач
Путешествие в историю математики. Решение старинных задач Прямоугольные треугольники
Прямоугольные треугольники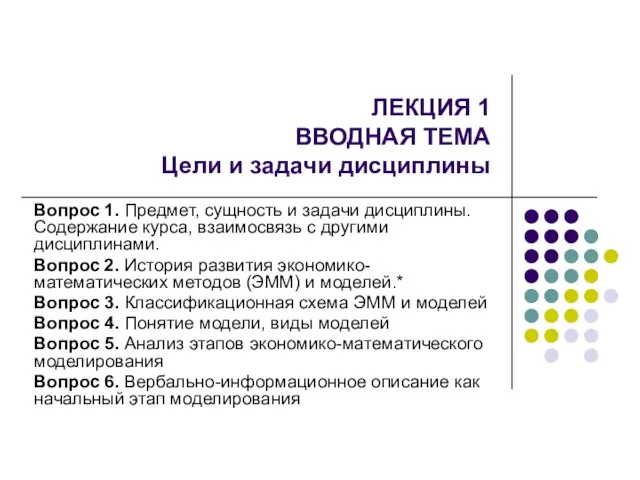 История развития экономико-математических методов (ЭММ) и моделей. Лекция 1
История развития экономико-математических методов (ЭММ) и моделей. Лекция 1 Презентацию подготовила Кулагина В.В. Учитель начальных классов ФКОУ СОШ имени А.Н.Радищева Г. Кузнецк-12 2012г.
Презентацию подготовила Кулагина В.В. Учитель начальных классов ФКОУ СОШ имени А.Н.Радищева Г. Кузнецк-12 2012г. Округление десятичных дробей. Опорные конспекты
Округление десятичных дробей. Опорные конспекты Подборка заданий по геометрии за курс 7 класса
Подборка заданий по геометрии за курс 7 класса Задачи с цифрами 1, 5, 9
Задачи с цифрами 1, 5, 9 Математика в медицине
Математика в медицине Векторное произведение векторов
Векторное произведение векторов