Содержание
- 2. ЗВИЧАЙНІ диференціальні рівняння Звичайним диференціальним рівнянням називають рівняння, що зв'язує між собою значення незалежної змінної x,
- 3. ЗДР першого порядку Звичайним диференціальним рівнянням першого порядку називаються рівняння виду: де x - незалежна змінна,
- 4. Рівняння з відокремлюваними змінними Так називаються рівняння виду f(x)dx + g(y)dy = 0, Інтегруємо, отримаємо -
- 5. Однорідні рівняння так називаються рівняння виду Ці рівняння легко зводяться до рівнянь з відокремлюваними змінними: Записуємо
- 6. Виразимо у з останнього виразу як функцію х, отримаємо загальний розв'язок: Приклад:
- 7. Рівняння з однорідною правою частиною. Так називаються рівняння зі спеціальним видом залежності функції f(x, y) від
- 8. Приклад: - загальний розв'язок рівняння
- 9. Остаточно, отримаємо загальний розв'язок: Приклад:
- 10. Лінійні рівняння ДР першого порядку називається лінійним, якщо невідома функція y(x) і її похідна входять до
- 11. Для розв'язання рівняння представимо y(x) в вигляді добутку двох нових невідомих функцій u(x) і v(x): y(x)
- 12. Відмітимо, що розв'язуючи рівняння на v(x) ми не вводимо в цей розв'язок довільну сталу C, нам
- 13. Приклад: Розв'язання: і загальний розв'язок рівняння .
- 14. Для знаходження частинного розв'язку, що відповідає початковим умовам (задача Коші), підставимо в загальний розв'язок Розв'язок задачі:
- 15. Рівняння в повних диференціалах так називається рівняння виду (P(x, y), Q(x, y) - неперервно диференційовані) у
- 16. Для знаходження функції u(x, y) розв'язується система рівнянь з першого рівняння цієї системи знаходимо: з точністю
- 17. Приклад: знайти загальний розв'язок рівняння Впевнимся, що це - рівняння в повних диференціалах. .
- 18. ЗДР вищих порядків Звичайним диференціальним рівнянням називається рівняння, що зв'язує між собою значення незалежної змінно x,
- 19. Деякі типи рівнянь, що допускають пониження порядку. Рівняння виду розв'язується послідовним n-кратним інтегруванням. Перепозначивши сталі, загальний
- 20. Рівняння, не містить в явному вигляді невідому функцію та похідні нижчого порядку. Порядок рівняння виду F(x,
- 21. Приклад: Понизити порядок рівняння: Найменша похідна, що входить в явній формі до рівняння, - друга, тому
- 22. Рівняння, що не містить в явному вигляді незалежну змінну x. Порядок рівняння що не містять явно
- 23. Лінійні однорідні диференціальні рівняння другого порядку із сталими коефіцієнтами
- 27. Лінійні неоднорідні диференціальні рівняння другого порядку із сталими коефіцієнтами
- 32. Лінійні неоднорідні диференціальні рівняння другого порядку із сталими коефіцієнтами та спеціальною правою частиною
- 47. Скачать презентацию












































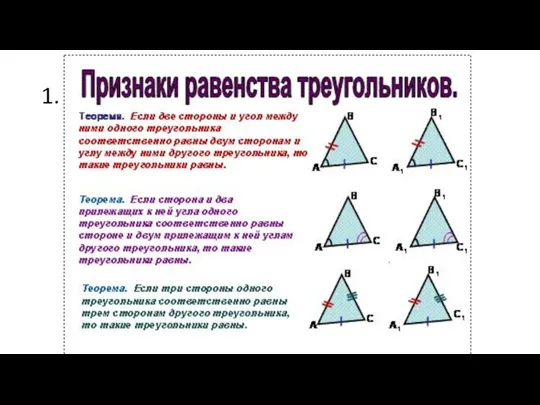 Признаки равенства треугольников
Признаки равенства треугольников Дифференциальные уравнения высших порядков
Дифференциальные уравнения высших порядков Параллельность прямых и плоскостей (10 класс)
Параллельность прямых и плоскостей (10 класс) Умножение обыкновенных дробей
Умножение обыкновенных дробей TA&Ml_ukr_1
TA&Ml_ukr_1 Инженерно-вычислительные технологии
Инженерно-вычислительные технологии Применение производной к исследованию функции
Применение производной к исследованию функции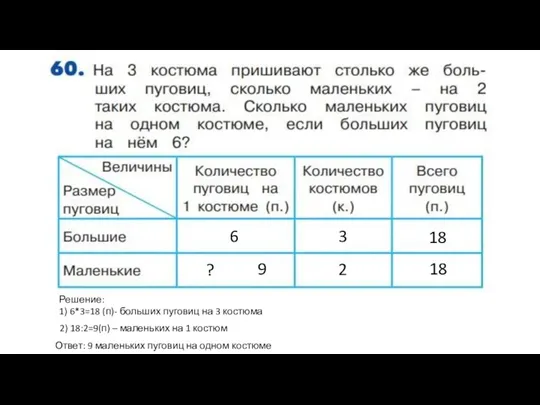 Задача о костюмах
Задача о костюмах Нахождение неизвестного вычитаемого
Нахождение неизвестного вычитаемого Дискретные случайные величины
Дискретные случайные величины Задание В11, открытого банка ЕГЭ по математике (часть 1)
Задание В11, открытого банка ЕГЭ по математике (часть 1) Критерий линейной корреляции Пирсона
Критерий линейной корреляции Пирсона Построение сечений
Построение сечений Логарифмические уравнения и методы их решения
Логарифмические уравнения и методы их решения Решение уравнений сводящихся к линейным
Решение уравнений сводящихся к линейным Золотое сечение в архитектуре, скульптуре, живописи
Золотое сечение в архитектуре, скульптуре, живописи Задачи на построение
Задачи на построение Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже
Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже Презентация на тему Сложение и вычитание чисел 5,6,7,8,9 (1 класс)
Презентация на тему Сложение и вычитание чисел 5,6,7,8,9 (1 класс)  Равносильные уравнения и неравенства
Равносильные уравнения и неравенства Компланарные векторы
Компланарные векторы Цветочное настроение (порядковый счет)
Цветочное настроение (порядковый счет) Венегрет. Урок
Венегрет. Урок Презентация по математике "Портреты учёных математиков" -
Презентация по математике "Портреты учёных математиков" -  График функций. Домашняя работа по алгебре
График функций. Домашняя работа по алгебре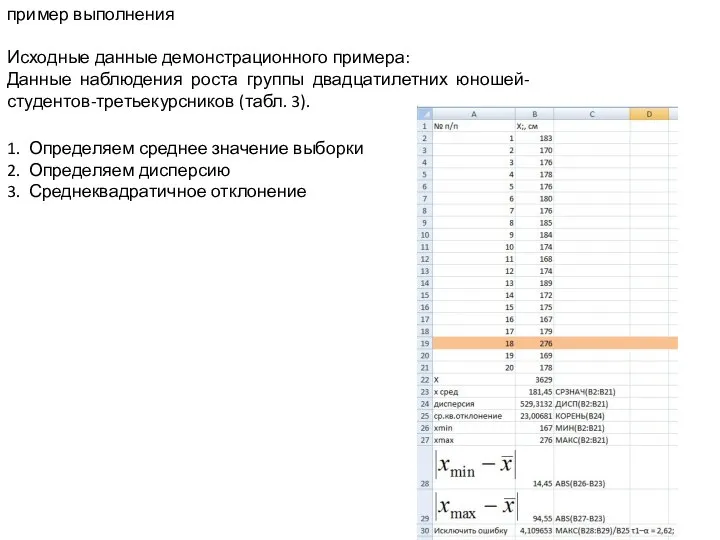 Данные наблюдения роста группы двадцатилетних юношей студентов
Данные наблюдения роста группы двадцатилетних юношей студентов Ломаная линия
Ломаная линия Решение тригонометрических уравнений. 10 класс
Решение тригонометрических уравнений. 10 класс