Содержание
- 3. Примеры применения этих формул
- 4. Найти первообразную функций
- 5. Найти первообразную функций
- 7. Неопределенный интеграл Совокупность всех первообразных данной функции f(x) называется ее неопределенным интегралом и обозначается : ,
- 8. Правила интегрирования
- 9. Свойства интеграла, вытекающие из определения Производная неопределенного интеграла равна подынтегральной функции, а его дифференциал- подынтегральному выражению.
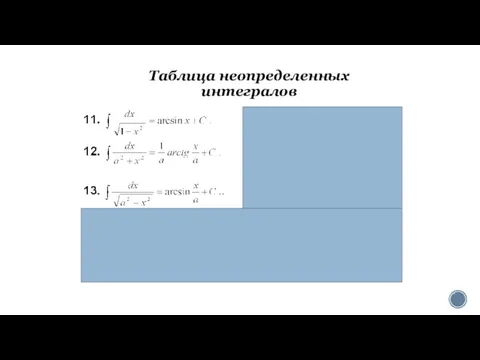
- 10. Таблица неопределенных интегралов
- 11. Таблица неопределенных интегралов
- 12. Примеры
- 13. Примеры
- 15. Скачать презентацию











 Геометрические фигуры: круг, квадрат, треугольник
Геометрические фигуры: круг, квадрат, треугольник Цветочное настроение (порядковый счет)
Цветочное настроение (порядковый счет) Нахождение числа по доле и доли по числу
Нахождение числа по доле и доли по числу Квадрат. Свойства и признаки квадрата
Квадрат. Свойства и признаки квадрата Действия над обыкновенными дробями. Счет и вычисления
Действия над обыкновенными дробями. Счет и вычисления Цифры в буквах
Цифры в буквах 15 задание. Виды. Делимость. Числовая последовательность. Конъюнкция. Множества
15 задание. Виды. Делимость. Числовая последовательность. Конъюнкция. Множества Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Презентация по математике "Решение задач с помощью систем уравнений второй степени" -
Презентация по математике "Решение задач с помощью систем уравнений второй степени" -  Дидактическая игра. Веселый ёжик
Дидактическая игра. Веселый ёжик Построение графиков функций
Построение графиков функций Показательные уравнения и неравенства
Показательные уравнения и неравенства Презентация на тему Мнимая единица
Презентация на тему Мнимая единица  Подготовка к контрольной работе. Изображение промежутков и запись их в виде неравенств
Подготовка к контрольной работе. Изображение промежутков и запись их в виде неравенств Уравнение
Уравнение Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника
Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника Zaokrugljivanje decimalnih brojeva
Zaokrugljivanje decimalnih brojeva Дифференциал и его приложение к приближённым вычислениям
Дифференциал и его приложение к приближённым вычислениям Окружность и круг
Окружность и круг Функции у=|x| и ей график
Функции у=|x| и ей график Логарифм числа и его свойства
Логарифм числа и его свойства 概率论与数理统计
概率论与数理统计 Урок математики во 2 классе
Урок математики во 2 классе Проценты
Проценты Статистика, вероятность, помеха, точность
Статистика, вероятность, помеха, точность Prezentatsia_Microsoft_PowerPoint(1)
Prezentatsia_Microsoft_PowerPoint(1) Презентация на тему РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ
Презентация на тему РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ  Презентация на тему Признаки делимости от 2 до 15
Презентация на тему Признаки делимости от 2 до 15