Содержание
- 2. 1.Числовые ряды. Определение. 2.Необходимый признак сходимости. 3.Достаточные признаки сходимости рядов с положительными членами. 4.Знакопеременные ряды. 5.Знакочередующиеся
- 3. Сумма ряда или ряд, — математическое выражение, позволяющее записать бесконечное количество слагаемых и подразумевающее значение их
- 4. Пусть дана бесконечная последовательность чисел: (1) Выражение: (2) называется числовым рядом, а числа - членами ряда.
- 5. Если последовательность частичных сумм имеет конечный предел (3) то этот предел называется суммой ряда. В этом
- 6. Необходимый признак сходимости ряда ● Если ряд сходится, то его общий член к нулю при стремится
- 7. Достаточные признаки сходимости рядов с положительными членами. 1) Признак сравнения рядов (5) (6) ● Если, начиная
- 8. 2) Признак Даламбера. ● Если существует предел то при ℓ ряд (5) сходится , о сходимости
- 9. Примеры 1. Написать пять первых членов ряда по данному общему члену (*) 2. Найти для ряда
- 10. Частичная сумма ряда Отсюда следует, что ряд (*) сходится и его сумма S=1 3. Написать формулу
- 11. Учитывая, что знаки членов ряда чередуются, получим если ,то расходится! => ряд расходится - расходиться! 4.
- 12. 5. Исследовать по признаку Даламбера сходимость ряда: ℓ=0 ряд сходится. 6. Исследовать по признаку Коши сходимость
- 13. Знакопеременные ряды Определение: Если члены числового ряда с разными знаками, то такой ряд будет называться знакопеременным.
- 14. ● Если же ряд (1) сходится, а ряд (2) расходится, то ряд (1) называется условно сходящимся.
- 15. Знакочередующиеся ряды Ряд (3) (3`) где n>0 (n=1,2,3,…) называется знакочередующимся. Этот ряд является частным случаем знакопеременного
- 16. Признак Лейбница Если члены знакочередующегося ряда (3) убывают по абсолютной величине и 0 , то такой
- 17. Члены данного ряда убывают по абсолютной величине, знаки чередуются и предел =>ряд сходится Составлен ряд (а)
- 18. Итак: 1) Сходятся условно ряды с общим членом или 2) Абсолютно сходятся ряды с общим членом
- 20. Скачать презентацию

















 Комбинаторика. Курс лекций Дискретная математика
Комбинаторика. Курс лекций Дискретная математика Применение интеграла к вычислению физических величин
Применение интеграла к вычислению физических величин Действительный анализ. Глава 2. Измеримые множества
Действительный анализ. Глава 2. Измеримые множества Предмет и метод статистики
Предмет и метод статистики Геометрические преобразования в пространстве
Геометрические преобразования в пространстве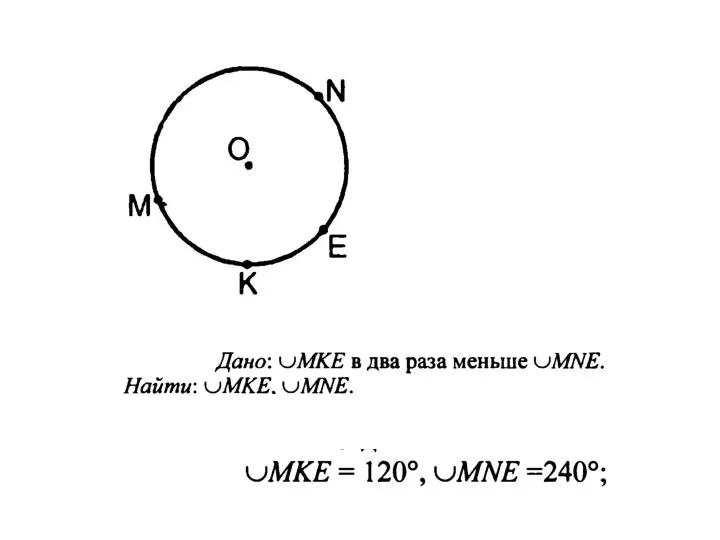 Теорема о вписанном угле
Теорема о вписанном угле Мультиколлинеарность
Мультиколлинеарность Презентация на тему Арифметические действия с дробями
Презентация на тему Арифметические действия с дробями  Знакомимся с многоугольниками
Знакомимся с многоугольниками Логические выражения. ДЗ
Логические выражения. ДЗ Роберт Гук
Роберт Гук Перпендикулярность в архитектуре
Перпендикулярность в архитектуре Показательная функция
Показательная функция Нахождение sin и tg
Нахождение sin и tg Тригонометрические формулы суммы и разности углов
Тригонометрические формулы суммы и разности углов Теорема о прямой, перпендикулярной к плоскости
Теорема о прямой, перпендикулярной к плоскости Работа по математике. Симметрия
Работа по математике. Симметрия Векторы в пространстве
Векторы в пространстве Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Презентация на тему Звездчатые многогранники
Презентация на тему Звездчатые многогранники  Вероятность события 9 класс
Вероятность события 9 класс Приемы быстрого счёта в математике
Приемы быстрого счёта в математике Равносильность уравнений. 11 класс
Равносильность уравнений. 11 класс Прямоугольник
Прямоугольник Площади геометрических фигур
Площади геометрических фигур Презентация на тему Сравнение, сложение, вычитание, умножение, деление десятичных дробей
Презентация на тему Сравнение, сложение, вычитание, умножение, деление десятичных дробей  Численное интегрирование
Численное интегрирование Письменное умножение двух чисел, оканчивающихся нулями
Письменное умножение двух чисел, оканчивающихся нулями